MOE是Mixture of Experts的缩写,也就是混合专家模型。
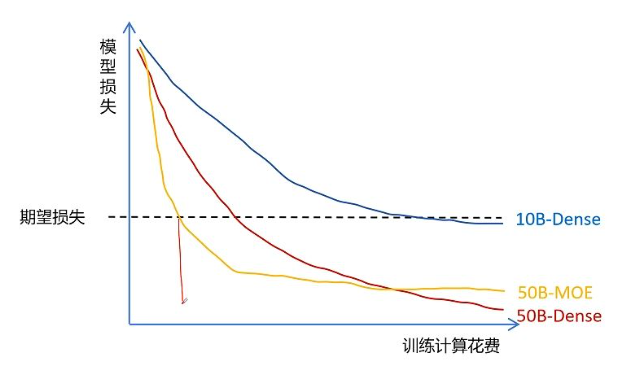
在预训练一个大模型时,如果你首先设定一个期望损失,也就设定你期望的模型表现效果,那么增大模型的参数量,在达到相同的期望效果时,花费的训练代价会更少,但是在推理阶段时,更大参数量的模型花费会更大。训练只有一次,但是推理是无数次的。
MOE模型在达到同样期望的效果时,训练花费计算会更少,而且最终推理时花费的计算代价也非常少。
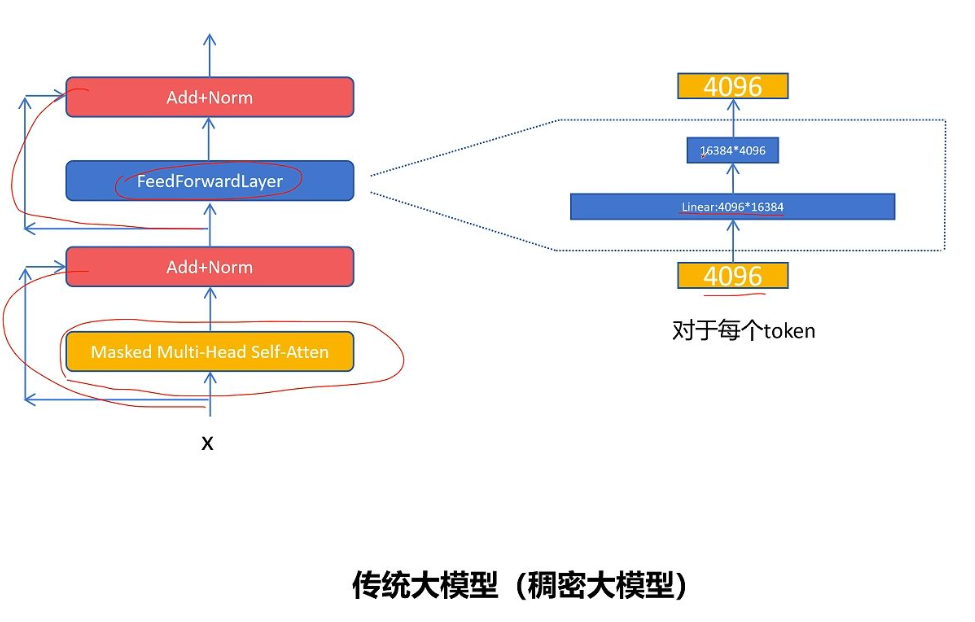
一个传统decode only的稠密大模型结构,首先是一个 带掩码的自注意力机制模块 和 残差连接与层归一化,接下来是一个 全连接FFN(feed forward layer)前向传播层 和 残差连接与层归一化。moe主要对FFN前向传播层进行改造,它的内部结构很简单,有两个线性层,第一个线性层会进行升维,一般会是原来的2倍到4倍,第二个线性层会进行降维,变化为原始的特征维度。例如:token输入是维度是4096,中间隐变量维度是16384,输出维度是4096.
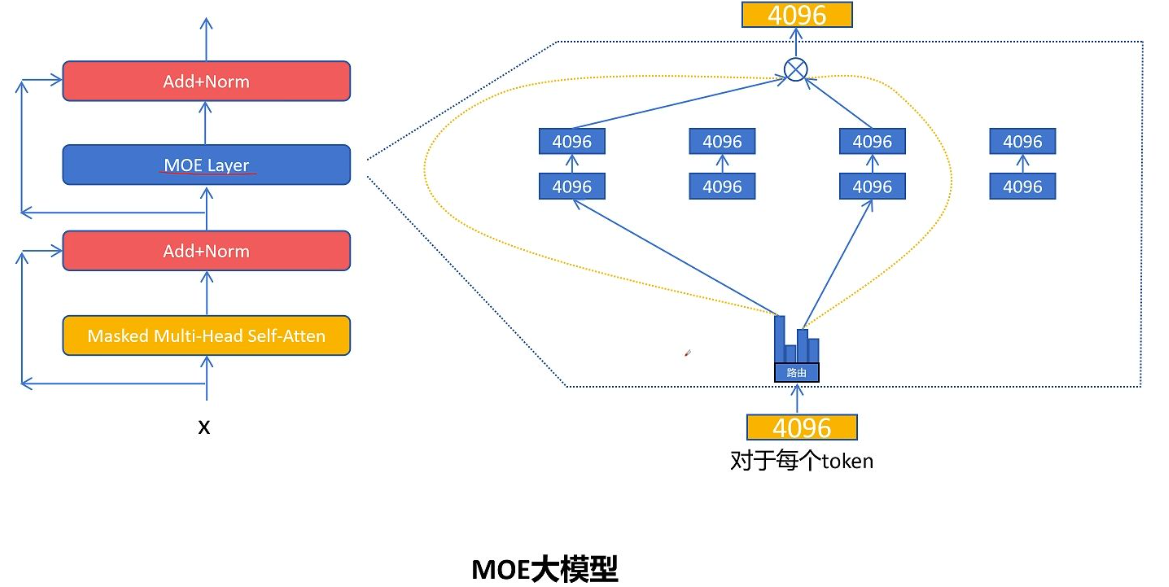
接下来我们就看一下MOE是如何改造FFN前向传播层,首先原来的一个FFN被拆分多个小的FFN,相比稠密大模型的FFN第一层的维度大幅减少,这里每一个小的FFN就被称为一个专家Expert。
那对于每个输入的token应该选择走哪个专家网络呢?这里就需要一个路由网络来决定。路由网络输出每个token走不同专家网络的概率值,然后找出其中排名靠前的几个专家。具体选择几个专家,这也是一个可以调节的超参数,比如这里选择的是排名靠前的2个专家,然后让token的特征通过选择的前2个专家网络,得到两个维度为4096的特征向量,然后再根据路由网络输出的专家权重(概率值)进行加权求和,这就得到了混合专家层最终对这个token的输出。这里值得注意的是,专家的选择是对每个token进行的,不是对整个序列。
代码实现
# 伪代码示例:MOE专家网络 class Expert(nn.Module):""" An MLP is a simple linear layer followed by a non-linearity i.e. each Expert """def __init__(self, n_embd):super().__init__()self.net = nn.Sequential(nn.Linear(n_embd, 4 * n_embd),nn.ReLU(),nn.Linear(4 * n_embd, n_embd),nn.Dropout(dropout),)def forward(self, x):return self.net(x)# 伪代码示例:MoE路由网络实现 class MoEGating(nn.Module):def __init__(self, input_dim, num_experts):super().__init__()self.gate = nn.Linear(input_dim, num_experts)def forward(self, x):# 计算专家权重(Softmax归一化)logits = self.gate(x)probs = torch.softmax(logits, dim=-1)# Top-2专家选择(避免所有计算集中在少数专家)top_k_probs, top_k_indices = torch.topk(probs, k=2)return top_k_probs, top_k_indices
MOE 特点
相同计算代价下,可以增大网络参数规模,性能更好。
基本可以达到相同参数规模的稠密网络性能。
相比同等参数规模的稠密网络,计算代价变小。
相比同等参数规模的稠密网络,显存占用不变。
可能有专家负载不均衡问题,训练难度增大。
MOE网络在训练时比稠密网络要难,因为会有专家负载不均衡的问题,可能大量的token都被少数的几个专家网络处理,而其他的专家占用了网络参数却不被激活,为了让MOE模型里的专家负载均衡,人们使用了想了很多办法:
专家负载均衡
1. 训练时对每个token最少选择2个专家。选择Top1专家和在剩余专家里按概率再选择一个。
2. 给每个专家设置token容量,达到容量后,则跳过处理,输出为全0。通过残差连接后边。
3. 设置一个负载均衡的辅助损失,让模型在训练过程中自己学会负载均衡
负载均衡损失
希望每个专家被调用的频率是相等的。
\( f_i = \frac{(\text{该专家被调用的次数})}{(\text{所有专家被调用的次数})} \)
\( loss_{\text{balance}} = \sum_{i = 1}^{N} (f_i)^2 \)
假设有2个专家:
\( f_1 = 1 \); \( f_2 = 0 \); \( loss_{\text{balance}} = 1^2 + 0^2 = 1 \)
\( f_1 = 0.8 \); \( f_2 = 0.2 \); \( loss_{\text{balance}} = 0.8^2 + 0.2^2 = 0.68 \)
\( f_1 = 0.5 \); \( f_2 = 0.5 \); \( loss_{\text{balance}} = 0.5^2 + 0.5^2 = 0.5 \)
这里可以通过柯西不等式来证明 当负载均衡时,loss取最小值。然而这个损失函数却不能直接拿来利用,因为我们计算每个专家被调用的频率,需要统计每个专家被调用的次数,而每个专家是否被调用是通过topk操作进行的。topk操作是根据权重进行的一个选择操作,它是不可微的,无法通过梯度下降进行优化。

所以有一个近似的做法,就是把频率的平方中的一个频率$f_i$用$p_i$来代替,$p_i$是一个批次中所有token对该专家的路由概率的平均值。理论上对该专家的路由的平均概率应该等于选择该专家的频率,同时路由的平均概率是通过softmax进行数据计算的得到的结果,它是可微的,可以通过梯度下降进行优化。所以最终的辅助负载均衡损失函数就为 每个专家的调用频率 * 路由概率的和。
DeepSeek-MOE
DeepSeekMoE论文题目为迈向让专家更加专精的MOE语言模型,可以看到DeepSeekMoE的改进点是让专家更加专精。
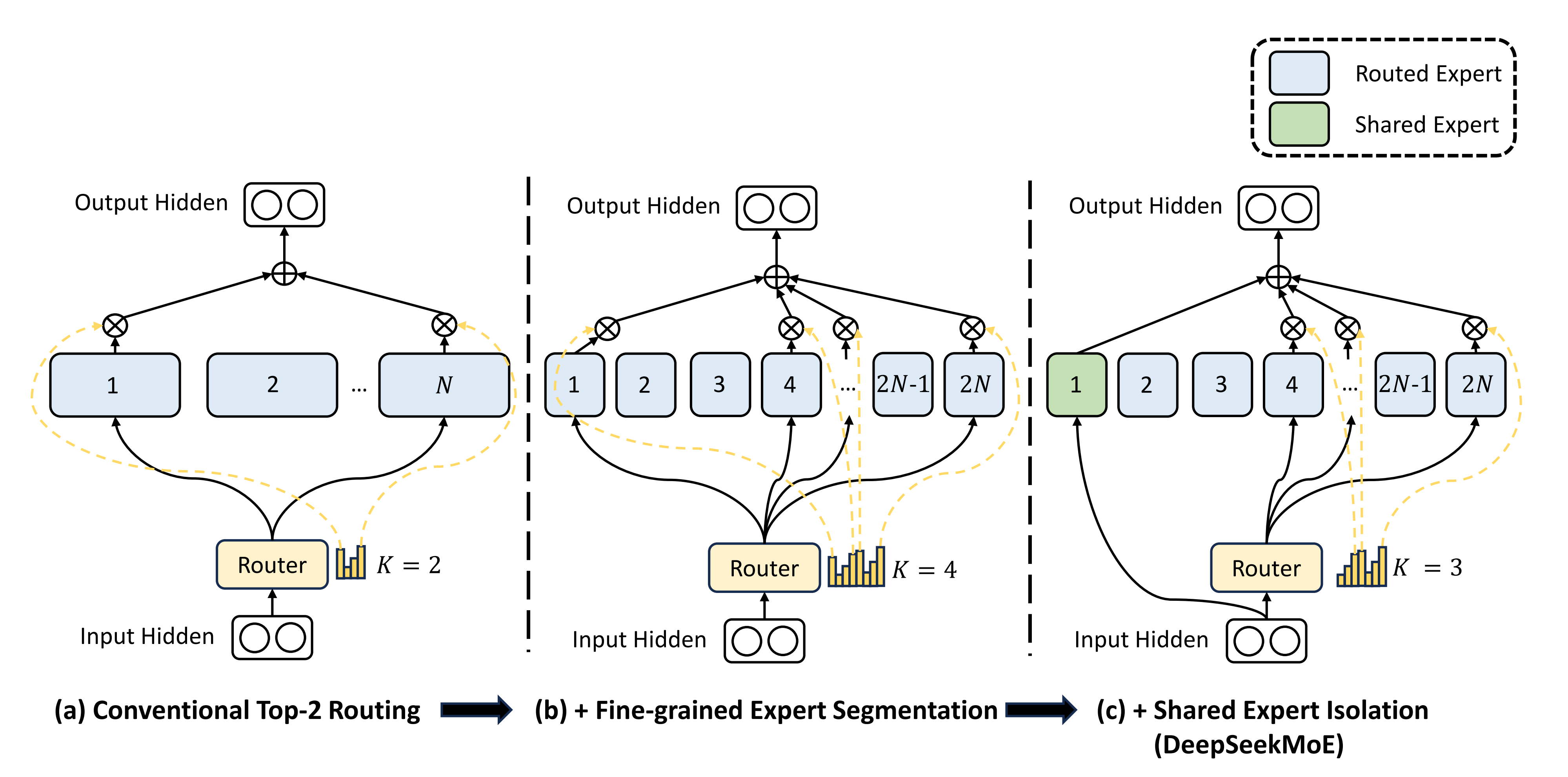
我们看一下基础的MOE实现,假设有n个专家每次选择2个专家,DeepSeek认为传统的MOE设置的专家数量太少了,导致每个专家学习到了过多彼此不想关的知识,从而不够专精。比如一个医院里面只有2名医生,那这2个医生需要掌握的医学领域就太广泛了,不利于他医术的精进。
DeepSeek想到的办法就是将专家进行更进一步的细分,同时每个专家的网络也变小,比如这里将原来的n个专家变为2n个专家,每个专家网络参数量也为原来专家的一半,这样在网络前向传播时,维持和之前网络同样的计算代价的前提下,就可以激活4个专家。假如原来有8个专家,激活2个专家,有28种组合;现在细分16个专家,激活4个专家,现在有1820种组合。可以看到对专家进行细分,可以得到更灵活的专家组合。
DeepSeek又进一步的想到,所有的专家可能都要学习一些基础的通用的能力,是否可以将所有专家都要学习的通用基础能力提取出来作为一个共享专家,共享专家保证每次都被激活,他负责所有专家原来都需要的通用能力,例如:医院里面的各个科室都需要验血,那就把验血作为一个共享的科室,其他所有的科室都可以进行调用。这里在细分的2n个专家里提取1个共享专家,它每次都被激活,然后再从剩下的2n-1个 专家选择k=3个专家,这样保证 路由专家+共享专家总数4个不变,和原来选择2个专家的原始MOE网络计算代价是相同的。
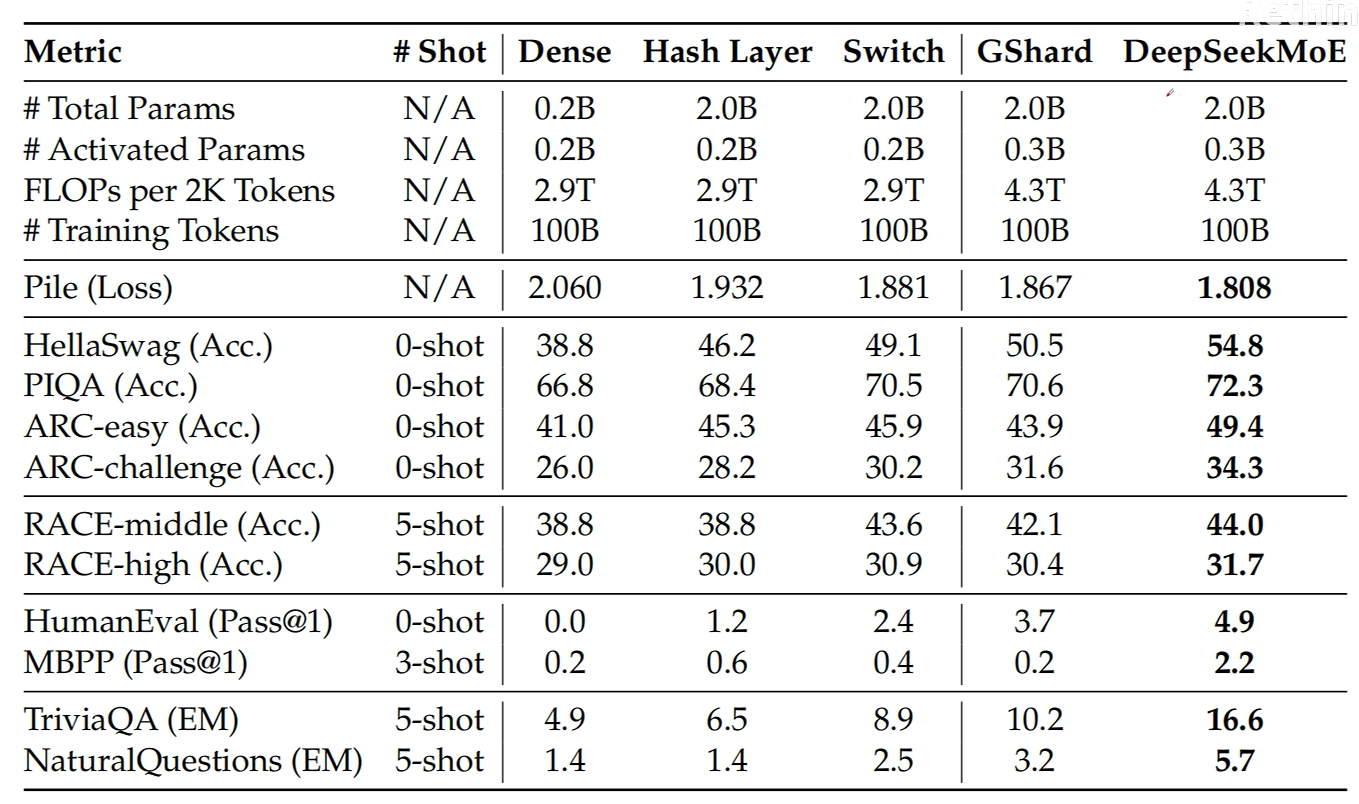
通过这些改进DeepSeekMoE的效果,它在同等计算代价的情况下比稠密网络和普通MOE的效果都有很大的提升。
代码实现
import torch import torch.nn as nnclass DeepseekMoE(nn.Module):"""混合专家模块(Mixture of Experts),包含可路由专家和共享专家核心思想:通过门控机制将输入分配给不同的专家网络处理,再融合结果,提升模型能力同时控制计算量"""def __init__(self, config):super().__init__()self.config = config # 保存配置参数(如专家数量、中间层维度等)# 每个token需要路由到的专家数量(例如k=2,表示每个token由2个专家处理)self.num_experts_per_tok = config.num_experts_per_tok# 初始化可路由专家列表:每个专家是一个MLP网络(DeepseekMLP)# 数量由config.n_routed_experts指定,每个专家的中间层维度为config.moe_intermediate_sizeself.experts = nn.ModuleList([DeepseekMLP(config, intermediate_size=config.moe_intermediate_size) for i in range(config.n_routed_experts)])# 门控网络:负责决策每个token应该路由到哪些专家self.gate = MoEGate(config)# 初始化共享专家(可选):所有token都会经过共享专家处理if config.n_shared_experts is not None:# 共享专家的中间层维度 = 单个专家维度 × 共享专家数量(放大容量)intermediate_size = config.moe_intermediate_size * config.n_shared_expertsself.shared_experts = DeepseekMLP(config=config, intermediate_size=intermediate_size)def forward(self, hidden_states):"""前向传播:将输入通过门控路由到专家,融合结果后输出Args:hidden_states: 输入的隐藏状态,形状通常为 [batch_size, seq_len, hidden_size]Returns:融合专家输出后的隐藏状态,形状与输入一致"""# 保存原始输入用于后续共享专家计算(残差类似的设计)identity = hidden_states# 记录原始形状,用于后续恢复维度orig_shape = hidden_states.shape# 门控网络计算:得到每个token需要路由的前k个专家索引、权重,以及辅助损失# topk_idx: 专家索引,形状通常为 [batch_size, seq_len, num_experts_per_tok]# topk_weight: 专家权重,形状与topk_idx一致,用于加权融合专家输出# aux_loss: 辅助损失(如负载均衡损失),用于训练时平衡专家的负载topk_idx, topk_weight, aux_loss = self.gate(hidden_states)# 展平输入的前两个维度(batch_size和seq_len合并),方便后续路由处理# 形状变为 [batch_size * seq_len, hidden_size]hidden_states = hidden_states.view(-1, hidden_states.shape[-1])# 展平专家索引,形状变为 [batch_size * seq_len * num_experts_per_tok]flat_topk_idx = topk_idx.view(-1)if self.training: # 训练阶段逻辑# 对输入进行复制:每个token需要路由到k个专家,因此复制k次# 形状变为 [batch_size * seq_len * num_experts_per_tok, hidden_size]hidden_states = hidden_states.repeat_interleave(self.num_experts_per_tok, dim=0)# 初始化空张量用于存储所有专家的输出y = torch.empty_like(hidden_states)# 遍历每个专家,处理分配给自己的tokenfor i, expert in enumerate(self.experts):# 筛选出路由到当前专家i的token,用当前专家处理并存储结果y[flat_topk_idx == i] = expert(hidden_states[flat_topk_idx == i])# 融合专家输出:将结果重塑为 [batch_size, seq_len, num_experts_per_tok, hidden_size]# 乘以专家权重(topk_weight)后按专家维度求和,得到每个token的最终输出y = (y.view(*topk_weight.shape, -1) * topk_weight.unsqueeze(-1)).sum(dim=1)# 恢复为原始输入形状 [batch_size, seq_len, hidden_size]y = y.view(*orig_shape)# 应用辅助损失(通常用于训练时平衡专家负载,不影响推理)y = AddAuxiliaryLoss.apply(y, aux_loss)else: # 推理阶段逻辑(通常更高效,避免冗余计算)# 调用推理专用函数处理,结果恢复为原始形状y = self.moe_infer(hidden_states, flat_topk_idx, topk_weight.view(-1, 1)).view(*orig_shape)# 如果存在共享专家,将共享专家的输出与路由专家的输出相加(类似残差连接)if self.config.n_shared_experts is not None:y = y + self.shared_experts(identity)return y
参考:https://www.bilibili.com/video/BV1uUPieDEK1
