前言
这回一改上次颓势。
T1一眼,T3思考2h+后场切。
但 T2 只有接近正解的 50 pts,T4 常数大挂了 20pts。
A
给定 \(n,k\),对 \([1,n]\) 建线段树后,求线段树上所有节点长度的 \(k\) 次方之和。
Solution
发现线段树上长度不同节点数量不会太大 \((O(\log n) \text{的样子})\)。
于是直接 map 存 (长度,出现次数) 的 pair,一层层做即可。
\(O(T\log n\log k\log\log n)\)。
B

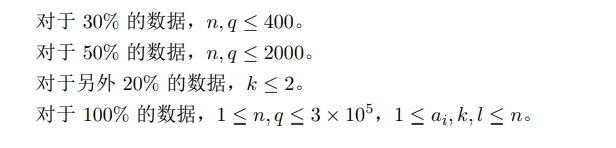
发现一个序列经历 \(O(\log \log n)\) 次操作可以被改成第一个数 \(=1\),其余全 \(0\) 的序列。
前 \(50\) pts 可以对每个前缀离线直接改。
\(100\) pts 加入数字的时候递归更改变化的位置即可。
\(O(n\log^2 n)\)。
namespace Subtask2 {int f[20][N],tot,S[20]={0};void Add(int o,int x,int v) {if(o>10) return ;if(f[o][x]) Add(o+1,f[o][x],-1);f[o][x]+=v;S[o]+=v;if(f[o][x]) Add(o+1,f[o][x],1);}void solve() {FOR(i,1,q) {int l=read(),k=read();vec[l].eb(k,i);}FOR(i,1,n) {Add(1,a[i],1);sort(vec[i].begin(),vec[i].end());for(auto p:vec[i]) {int k=p.fr,id=p.se;if(k>10) ans[id]=1;else ans[id]=S[k];}}FOR(i,1,q) printf("%d\n",ans[i]);}
}
C


Solution
发现当 \(k=1\) 时等价于查询树状数组的那个 \(c\) 数组的第 \(x\) 项。
我们把树状数组那个树建出来。
我们发现,一次查询 \(x\; k\),必定是 \(x\) 的子树中所有点的权值乘上某个系数 \(q_x\) 之和。
即 \(ans_{x,k}=\displaystyle\sum_{y\in \operatorname{Tree}(x)} a_y\times q_y\)。
发现 \(q\) 即相当于初始 \(q_x=1,q_i=0(i\ne x)\),之后在树上对 \(q\) 做 \(k\) 次前缀和。
设 \(f_{i,j}\) 表示考虑到前缀和第 \(i\) 项,当前是第 \(j\) 次前缀和,\(q_i\) 的值。
\(f_{0,0}=1\)。
发现这玩意很像网格左上角走到 \((i,j)\) 的方案数转移方程,故 \(f_{i,j}=C_{i+j-2}^{j-1}\)。
于是 \(ans_{x,k}=\displaystyle\sum_{y\in \operatorname{Tree(x)}} C_{dep_y+k-2}^{k-1}a_y\)。
考虑拆式子。
由于树状数组的树深度不超过 \(O(\log n)\),故可以枚举深度,此时前面的组合数为定值。
而后面一项可以预处理。
单点增加直接暴力跳父亲更新即可。\(O((n+m)\log n)\)。
赛时代码。
namespace Subtask2 {int fa[N],dep[N];LL power(LL a,LL b) {LL res=1;for(;b;b>>=1) {if(b&1) res=1LL*res*a%Mo;a=a*a%Mo;}return res;}LL s[N][23],Invdp[30];void Add(LL &x,int y) {x+=y;while(x>=Mo) x-=Mo;}void Upt(int x,int v) {int dp=1;while(x) {Add(s[x][dp],v);++dp;x=fa[x];}}LL Ask(int x,int k) {LL Answer=0,C=1;FOR(dp,1,21) {Answer=(Answer+1LL*s[x][dp]%Mo*C%Mo)%Mo;C=C*Invdp[dp]%Mo*(dp+k-1)%Mo;}return Answer;}void solve() {FOR(i,1,21) Invdp[i]=power(i,Mo-2);FOR(i,1,n) if(i+(i&-i)<=n) fa[i]=i+(i&-i);FOR(i,1,n) Upt(i,a[i]);while(m--) {int op=read(),x=read(),v=read();if(op==1) Upt(x,v);if(op==2) printf("%lld\n",Ask(x,v));}}
}
