前验概率与后验概率
前验概率(Prior Probability)和后验概率(Posterior Probability)是一对孪生概念,它们是贝叶斯统计思想的核心。简单地说,前验是“你原本的信念”,后验是“在看到证据之后你修正过的信念”。我们来一步步拆解。
一、前验概率:在看到数据之前的信念
定义:前验概率是指在没有观察到新的数据之前,我们对某个事件或假设的先验相信程度。
数学上记作:
\(
P(H)
\)
其中 ( H ) 表示一个假设(例如“病人有病”)。
举例:
假设一种疾病在总体人群中的发病率是 1%。
这意味着在不知道某个人的检测结果之前,
你认为“他得病”的概率是:
\(
P(\text{有病}) = 0.01
\)
这就是前验概率。
它来自经验、统计历史、或专家知识,是在任何新证据出现前的认知状态。
二、后验概率:看到数据之后的信念
定义:后验概率是指在观察到新的证据或数据之后,我们对某个假设的修正后概率。
数学上:
\(
P(H | D)
\)
表示“在看到数据 ( D ) 后,假设 ( H ) 成立的概率”。
它通过贝叶斯公式计算:
\(
P(H | D) = \frac{P(D | H) \cdot P(H)}{P(D)}
\)
其中:
- ( P(H) ):前验概率(原本的信念)
- ( P(D | H) ):似然(如果假设为真,这个数据出现的概率)
- ( P(D)):归一化因子,保证结果是个概率
- ( P(H | D) ):后验概率(修正后的信念)
三、一个具体例子
假设某种疾病发病率是 1%,即 ( P(\text{有病}) = 0.01 )。
某个检测手段准确率很高:
- 有病的人检测呈阳性的概率:( P(\text{阳性}|\text{有病}) = 0.99 )
- 无病的人误检阳性的概率:( P(\text{阳性}|\text{无病}) = 0.05 )
现在某人检测结果为阳性,我们想知道他真正有病的概率是多少?
\(
P(\text{有病}|\text{阳性}) = \frac{P(\text{阳性}|\text{有病}) \cdot P(\text{有病})}{P(\text{阳性})}
\)
其中:
\(
P(\text{阳性}) = P(\text{阳性}|\text{有病})P(\text{有病}) + P(\text{阳性}|\text{无病})P(\text{无病})
\)
代入:
\(
P(\text{阳性}) = 0.99\times0.01 + 0.05\times0.99 = 0.0099 + 0.0495 = 0.0594
\)
于是:
\(
P(\text{有病}|\text{阳性}) = \frac{0.99\times0.01}{0.0594} \approx 0.1667
\)
也就是说,即使检测为阳性,你真正有病的概率也只有约 16.7%。
这就是后验概率——用数据更新过的信念。
联合概率理解:A(骰子投到6), B(硬币掷出反面朝上),那么联合概率为\(P(A, B)\)
生成模型
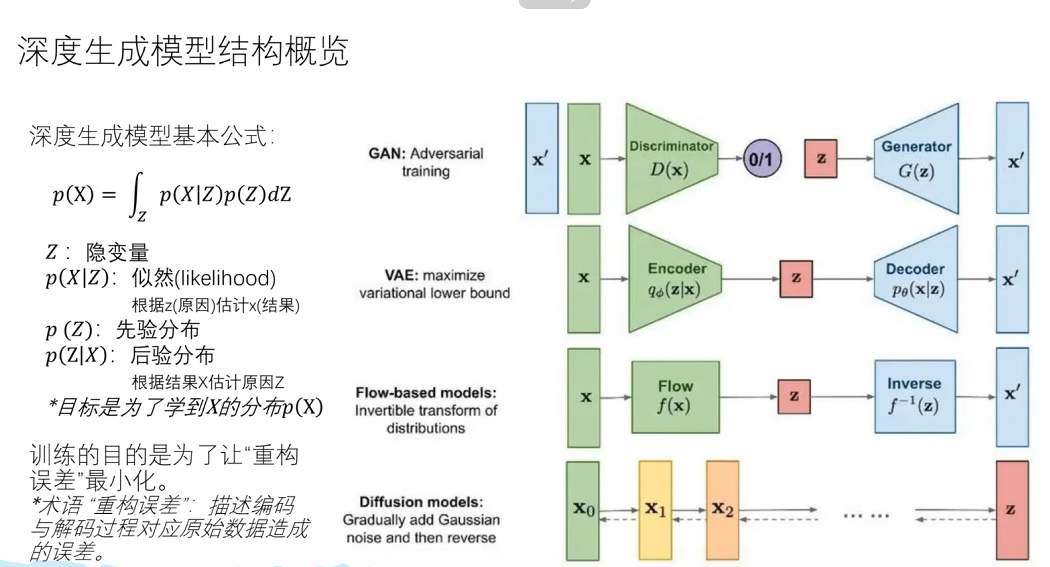

扩散模型
参考:https://cloud.tencent.com/developer/article/2395603
GAN的模式崩溃:生成器没有学会所有模式,只盯上了其中一小部分。数据集中有各种动物(猫、狗、鸟);理想的生成器应能生成多样化样本;但训练后,它只会生成“狗”——甚至只会生成同一只狗的某个角度。此时生成器的输出分布只覆盖了真实分布的一部分模式。
-
正向扩散:定义一个马尔可夫过程,给图片添加噪声的过程,每一步都把上一步的图像稍微“模糊”一点,直到接近于标准高斯噪声。由于每一步都是高斯线性加噪,所以可以直接写出从第 0 步到第 t 步的结果。这意味着我们可以直接采样任意时刻的噪声版本,无需真的一步步加噪。
-
反向扩散:去除噪声,还原真实图片。理论上要想从噪声还原到数据,我们需要逆转这个过程,但是很不好算。实际上,引入一个神经网络(通常是 U-Net),去近似这个逆过程的均值,核心目标是让模型学会预测噪声。也就是说,模型在学“去噪”的能力。
clip
文生图和图生文都是经典的多模态问题,为了
