本文档深入探讨了如何利用光学原理进行高效计算,特别是针对现代AI模型中常见的卷积和矩阵乘法操作。内容涵盖了从加速卷积的深层数学基础,到实现这些计算的各种前沿光学器件,最后对光学加速器与传统GPU进行了系统级的比较与展望。
一、 卷积计算的数学加速原理:FFT的魔法
长卷积运算是许多现代AI模型(如Hyena)的核心,其计算复杂度通常是 O(n²)。然而,通过快速傅里叶变换(FFT),我们可以将其加速到 O(n log n)。其深刻的数学原理可以分四步理解。
第一步:卷积的本质——乘以一个托普利茨矩阵 (Toeplitz Matrix)
一个标准的1D卷积操作,在数学上完全等价于一个向量乘以一个托普利茨矩阵。该矩阵的特点是每条对角线上的元素都相同。
例如,输入信号 x = [x₁, x₂, x₃, x₄] 与卷积核 k = [k₁, k₂, k₃] 的卷积,可以写成矩阵乘法 y = T * x:
[ y₁ ] [ k₁ k₂ k₃ 0 ] [ x₁ ][ y₂ ] = [ 0 k₁ k₂ k₃ ] * [ x₂ ][ y₃ ] [ 0 0 k₁ k₂ ] [ x₃ ][ y₄ ] [ 0 0 0 k₁ ] [ x₄ ]
直接进行这个 n x n 矩阵乘法,需要 O(n²) 的计算量。
第二步:一个特殊的近亲——循环矩阵 (Circulant Matrix)
循环矩阵是托普利茨矩阵的“完美”版本,其特点是每一行都是前一行向右循环移位一个位置得到的结果。移出右边界的元素会从左边界“卷回来”(Wrap around)。
用卷积核 k = [k₁, k₂, k₃, 0] 构建的4x4循环矩阵 C 如下:
[ k₁ k₂ k₃ 0 ]
C = [ 0 k₁ k₂ k₃ ] <-- 与托普利茨矩阵不同,k₃循环到了最左边[ k₃ 0 k₁ k₂ ][ k₂ k₃ 0 k₁ ]
用循环矩阵 C 乘以信号 x,得到的是“循环卷积”。
第三步:FFT 的魔法——对角化循环矩阵
循环矩阵最神奇的性质是:任何循环矩阵都可以被傅里叶变换矩阵 F 对角化。
公式:C = F⁻¹ * D * F
C:循环矩阵F:离散傅里L叶变换(DFT)矩阵F⁻¹:逆傅里叶变换(IDFT)矩阵D:一个对角矩阵
这个公式意味着,计算 y = C * x 这个 O(n²) 的复杂操作,可以被分解为三步:
X_fft = F * x:对信号x做FFT (复杂度 O(n log n))Y_fft = D * X_fft:在频域做元素对元素相乘 (复杂度 O(n))y = F⁻¹ * Y_fft:对结果做逆FFT (复杂度 O(n log n))
更神奇的是,对角矩阵 D 的对角线元素,恰好就是卷积核 k 的傅里叶变换 K_fft。这完美印证了卷积定理:
时域的卷积 = 频域的乘积
conv(x, k) = IFFT( FFT(x) * FFT(k) )
第四步:最后的桥梁——将标准卷积伪装成循环卷积
我们想要计算的是标准卷积,但只有循环卷积能被FFT直接加速。解决方案是补零(Padding)。
通过将输入信号 x 和卷积核 k 都补零到一个足够大的长度(例如 n + m - 1,其中n和m是原始长度),我们构建一个更大的循环矩阵。在这个更大的体系中,当卷积核的元素“循环”回来时,它们只会与我们补充的零相乘,因此不会“污染”标准卷积的计算结果。
这正是“任何托普利茨矩阵都可以被嵌入到一个两倍大小的循环矩阵中”这句话的实际操作含义。
结论
整个逻辑链如下:
- 标准卷积等价于乘以一个托普利茨矩阵 (O(n²))。
- 我们发现乘以循环矩阵的循环卷积可以用FFT加速到 O(n log n)。
- 其原理是傅里叶变换能将循环矩阵对角化,把矩阵乘法变成元素乘法。
- 通过补零,我们可以将标准卷积问题转化为一个等价的循环卷积问题。
- 因此,我们可以用FFT来快速计算标准卷积,总复杂度为 O(n log n)。
二、 光学计算的物理实现:从经典到前沿
光学计算的核心在于利用光的物理特性(衍射、干涉、谐振等)来直接完成数学运算。
经典范例:什么是 4f 系统?
4f 系统是光学信息处理的经典教科书范例,用于实现空间滤波,其最常见的应用就是进行卷积运算。它的名字来源于其光路的总长度正好是四个焦距(focal length)。
[图:经典4f系统光路示意图]
一个典型的4f系统由以下部分组成:
- 输入平面 (Input Plane):放置输入信号,通常是一个加载了图像的空间光调制器(SLM)。
- 第一个透镜 (Lens 1):紧挨着输入平面。光穿过输入图像后,这个透镜会对光场进行傅里叶变换。
- 傅里叶平面 (Fourier Plane):位于第一个透镜的后焦平面处(距离透镜
f)。在这里,输入图像的频谱(空间频率分布)被清晰地呈现出来。我们在这里放置一个滤波片(Mask)。这个滤波片的设计直接对应着卷积核的傅里-叶变换。光穿过滤波片,相当于在频域完成了乘法。 - 第二个透镜 (Lens 2):位于距离傅里叶平面
f的地方。它接收经过滤波的光,并对其进行逆傅里叶变换。 - 输出平面 (Output Plane):位于第二个透镜的后焦平面处(距离透镜
f)。在这里得到的就是输入信号与卷积核进行卷积后的结果。
整个光路长度为 f (输入到透镜1) + f (透镜1到傅里叶平面) + f (傅里叶平面到透镜2) + f (透镜2到输出平面) = 4f。
主要挑战:4f系统体积庞大,对光学元件的对准要求极高,且其核心计算功能由一块通常静态的、无法编程的滤波片决定。
前沿光学计算器件
为了克服传统光学系统的挑战,现代光学计算已经发展出多种更精巧、强大且更具集成潜力的器件和架构。
1. 马赫-曾德干涉仪阵列 (Mach-Zehnder Interferometer, MZI Array)
这可能是目前最有潜力的通用矩阵乘法器,也是Lightmatter等公司技术的核心。
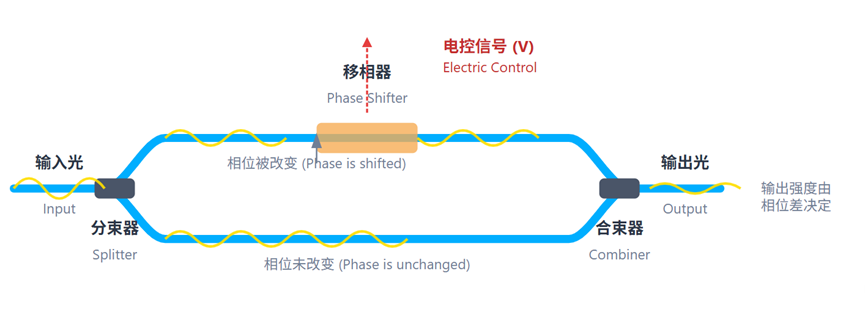
- 核心物理原理:光的干涉。一个MZI单元将光分成两束,通过电控移相器改变其中一束的相位,再将两束光合并。输出光强因干涉而改变,从而实现模拟乘法。
- 如何实现计算:单个MZI可实现一个2x2的可编程矩阵乘法。通过将大量MZI单元以网格状结构排列,可以构建出能实现任意N x N矩阵乘法的光学核心。
- 巨大优势:
- 完全可编程:通过电信号实时改变矩阵,解决了静态滤波片的难题。
- 高速度和低功耗:计算过程近乎瞬时,能耗远低于数字计算。
- 主要挑战:工艺复杂,对温度敏感,大规模扩展仍有挑战。
![image]()
[图1:MZI单元物理原理示意图]
2. 微环谐振器阵列 (Micro-ring Resonator, MRR Array)
这是另一种在光子芯片上实现滤波和调制的核心器件。
- 核心物理原理:光的谐振。当特定波长的光通过一个紧邻微环的波导时,如果该波长是微环的谐振波长,光就会被“捕获”进环内,导致该波长的光在直波导中被大幅衰减。
- 如何实现计算:利用波分复用(WDM)技术。
- 将输入向量
x的每个元素xᵢ编码到不同波长λᵢ的光上。 - 将这束“彩虹”光送入一个MRR阵列。
- 每个MRR被电调谐以精确控制一个特定波长
λᵢ的通过率,这个通过率就代表了权重wᵢ。 - 最终输出的各个波长的光强即为
wᵢ * xᵢ,并行地完成了元素对元素的乘法。
- 将输入向量
- AI计算应用:MRR阵列是为AI计算中的乘法步骤量身打造的。它可以高效执行全连接层、卷积层以及Transformer注意力机制中的大规模向量-矩阵或矩阵-矩阵乘法中的“乘法”部分。
- 巨大优势:
- 极高的并行度:一根波导可同时处理数百个波长通道。
- 极致的紧凑性:微环尺寸可达微米级,适合大规模集成。
- 主要挑战:对波长和温度极其敏感,需要精确的控制和校准。
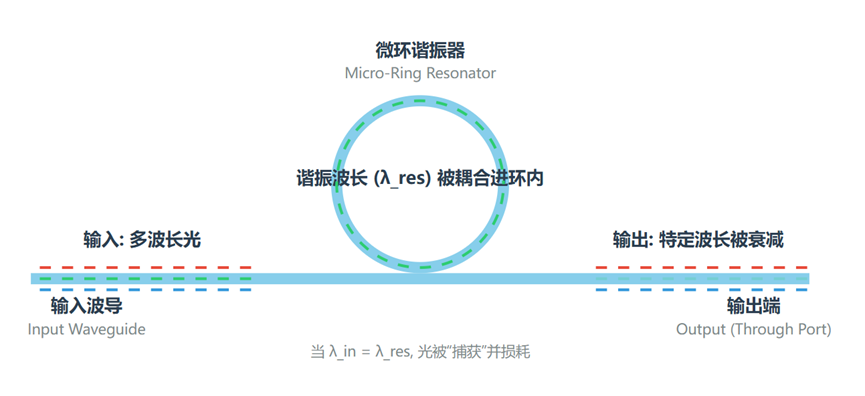
[图3 :微环谐振器阵列物理原理示意图]
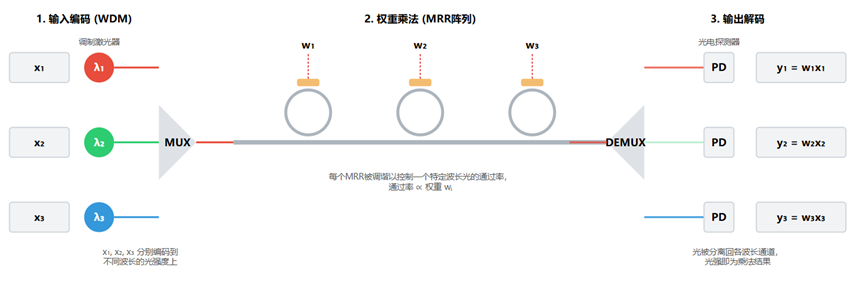
[图4 :微环谐振器阵列实现卷积计算示意图]
3. 超构表面/超构材料 (Metasurfaces / Metamaterials)
这是一个颠覆性的方向,试图将整个光学系统的功能压缩到一个二维平面上。
- 核心物理原理:由大量精心设计的、尺寸远小于光波长的纳米结构阵列构成。每个纳米结构都像一个独立的“相位控制器”,通过改变其几何参数,可以对入射光的相位、振幅和偏振进行像素级的精细调控。
- 如何实现计算:
- “一步式”卷积:可以直接设计一个超构表面,使其对光波前的变换函数等效于一个4f系统的全部功能(透镜1 + 滤波片 + 透镜2)。
- 模拟微分/积分:可设计特定的超构表面,直接对入射的图像光场进行数学运算,如边缘检测。
- 巨大优势:极致的紧凑性,为消费电子等领域提供了巨大想象力。
- 主要挑战与解决方案:动态可调谐
- 挑战:大多数超构表面是静态的,即“硬编码”了特定的数学运算。实现动态可调谐是其走向实用计算的关键。
- 核心思想:通过改变纳米结构本身或其周围环境的折射率,来主动、快速地改变其光学响应。
- 主流技术路线:
- 电调谐:利用载流子浓度调控(如TCO材料)或电光效应(如铌酸锂),速度快,最适合高速计算。
- 相变材料调谐:利用GST等材料在晶态和非晶态之间的光学属性剧变,可实现非易失性(状态可保持),适合可重构配置。
- 其他:热光调谐、液晶调谐、机械调谐等,各有优劣,但通常在速度或功耗上有限制。

[图2 :超构表面物理原理示意图]

[图3:超构表面实现一步式卷积与传统光学卷积对比图]
4. 数字微镜阵列 (Digital Micromirror Device, DMD)
这是一种已非常成熟的商用技术(广泛用于投影仪),也可作为强大的计算元件。
- 核心物理原理:光的反射。DMD由数百万个可独立高速翻转的微型镜片组成。
- 如何实现计算:在4f系统中,用DMD代替静态滤波片。通过电脑控制每个镜片的翻转,可以动态生成任意的二值(开/关)掩模,从而实现可编程的卷积。
- 巨大优势:技术成熟、高速、可靠、灵活。
各技术总结对比
| 光学器件/技术 | 核心物理原理 | 计算功能 | 关键优势 | 主要挑战 |
|---|---|---|---|---|
| 4f 系统 (经典) | 衍射、傅里叶光学 | 卷积/相关 | 原理清晰、易于理解 | 体积大、对准要求高、滤波片通常静态 |
| MZI 阵列 (光子芯片) | 光的干涉 | 通用矩阵乘法 | 完全可编程、高速、低功耗、可集成 | 工艺复杂、对热敏感、规模扩展性 |
| 微环谐振器 (光子芯片) | 光的谐振 | 权重乘法、滤波 | 波分复用并行度高、极紧凑 | 对波长和温度极敏感、调谐能耗 |
| 超构表面 | 亚波长散射 | 特定数学运算(卷积、微分) | 极致紧凑、一步式计算 | 大多为静态、动态调谐困难 |
| DMD | 光的反射 | 可编程滤波、矩阵乘法 | 技术成熟、高速、灵活 | 模拟精度有限(主要是二值)、体积较大 |
三、 系统级比较与展望
光学加速卡 vs. GPU (NVIDIA A100) 对比
无法简单地给出“1张A100 = X张光学卡”的等式,因其原理和适用范围完全不同。
-
核心计算能力:
- 光学卡:物理上构建为固定的
N x N矩阵(如256x256),一次完成一个N维矩阵-向量乘法。 - A100:通过软件(CUDA)灵活组合Tensor Core,处理任意尺寸的矩阵运算。
- 光学卡:物理上构建为固定的
-
计算精度 (最关键区别):
- 光学卡:本质是模拟计算,受物理噪声限制,有效精度通常在 4-8 bit 范围,适合低精度推理,难以用于高精度训练。
- A100:是数字计算,可提供从FP64到INT8的多种精确位深,通用性强。
-
峰值性能 (TOPS):
- 光学卡:理论峰值惊人。一个
256x256的MZI阵列若工作在10 GHz,理论性能可达1310 TOPS(在4-6 bit精度下)。 - A100:INT8峰值性能为
624 TOPS(带稀疏性可达1248)。
- 光学卡:理论峰值惊人。一个
结论:光学加速卡不是A100的直接替代品,而是一个专用协处理器。它在低精度推理的特定任务上,可能以极高的能效比(TOPS/W)超越A100,但无法完成高精度和通用计算任务。
光学加速卡的扩展 (Scale Up)
-
方案一:晶圆级/封装级横向扩展 (Scale-Up)
- 原理:在同一个硅基板或封装内,直接用光波导连接多个光子计算核心。数据以光的形式在核心间传输,无需“光-电-光”转换。
- 优势:超高带宽、超低延迟、能效极高,可构建巨大的单一计算资源池。
-
方案二:机柜与集群级横向扩展 (Scale-Out)
- 原理:利用光纤通信的天然优势,连接成大规模集群。未来甚至可能实现“全光网络”,计算结果不落地为电信号,直接在光域路由到下一个节点。
- 优势:可构建超大规模集群,传输距离远、能耗低。
PPCA 综合分析 (Performance, Power, Cost, Area)
| 指标 | GPU 加速卡 (如 NVIDIA A100) | 光学加速卡 (概念/原型) | 分析与展望 |
|---|---|---|---|
| Performance (性能) | 极高且灵活。支持从FP64到INT8的多种精度。通用性强。 | 理论峰值极高但受限。在低精度矩阵乘法上TOPS惊人,但精度低(4-8bit),功能单一。 | GPU是成熟的多面手,光学卡是偏科的“特长生”。未来可能是两者混合使用。 |
| Power (功耗) | 非常高 (400W-700W)。主要来自晶体管开关和数据搬运。 | 潜力巨大,有望极低。核心计算几乎不耗电。主要功耗来自激光器、温控和光电转换接口。能效比(TOPS/W)是其最大卖点。 | 光学计算的核心优势在于能效。若接口功耗降低,能效比有望高出GPU 1-2个数量级。 |
| Cost (成本) | 高昂。但得益于成熟的CMOS工艺和规模经济,单位算力成本在优化。 | 当前极高,未来不确定。研发、新材料、低良率、先进封装都导致成本高昂。 | GPU享有规模经济效应。光学卡的成本下降取决于制造工艺和产业链的成熟。 |
| Area (面积) | 巨大 (A100 Die Size: 826mm²)。 | 核心小,整体大。MZI阵列本身紧凑,但外围光电电路占据大量面积。 | 共封装光学(CPO)是减小整体面积的关键。计算密度仍需突破。 |
四、 最终总结
GPU和光学加速卡目前并非直接的竞争关系,更像是互补关系。
- GPU:如同强大的通用处理器,什么都能做,而且做得很好。
- 光学加速卡:则像一个专用协处理器,它只专注于一件事——高能效的低精度矩阵乘法,并力求做到极致。
在可预见的未来,最可能出现的场景是:一个服务器节点内同时包含CPU、GPU和光学协处理器(OPU)。CPU负责调度,GPU负责高精度和复杂的并行计算,而OPU则负责处理大模型推理中占据绝大多数算力的、海量的矩阵乘法运算,从而实现整个系统的性能与能效最优化。