[省选联考 2025] 图排列
闲话
一想到考场上自己以为直接输出最小 dfn 序就有 \(52pts\) 我就想笑。
洛谷题解区有一个码量小的分讨做法,但是因为我不想分讨所以还是选择了这个实现起来不太用脑子的做法(虽然思路很需要脑子)。
题解
跟着部分分做。
题意
先把题面翻译的人话一点:给定一张图,要求字典序最小的排列 \(p\) 满足对于 \(a<b<c<d\) 不能同时存在边 \((p_a,p_c),(p_b,p_d)\),换句话说就是按照这个排列的顺序把点排好之后不能存在在除了端点之外的地方相交的边。
树
显然 dfn 序一定合法,但这不一定最优。
首先我们肯定会把 \(1\) 放在第一位,然后考虑 \(1\) 的每棵子树,显然每棵子树都是占据一段连续的区间,任意两棵子树占据的位置不会相交,否则必然会出现相交的边。而两棵子树之间的顺序是任意的。
然后每棵子树就是一个独立的子问题了,我们在求出每棵子树的答案序列之后需要给这些子树分配区间,那显然就是按照第一个数从小到大排。
当然,我们在处理子问题的时候,假设处理的是 \(u\) 这棵子树,那么 \(u\) 不一定是像 \(1\) 这样放在第一个位置的,实际上 \(u\) 插在他的儿子子树之间的任意空隙都是可以的。
所以直接把 \(u\) 作为一个长度为 \(1\) 的答案序列扔进去一起排序即可。
Tip:实际上 \(u\) 子树的答案序列的第一个数一定是 \(u\) 子树中编号最小的点,但是不知道这一点也问题不大,无非就是写这档分的时候可以简单一点。
简单环
对于一个环 \(x_1,x_2,x_3,...,x_k\),环上的点在排列中的相对顺序一定是这个环的某个循环,换句话说如果我钦定了 \(x_1\) 是排列中最靠前的点,那么其他点在排列中的相对顺序只能是 \(x_2,x_3,..,x_k\) 或者 \(x_k,x_{k-1},...,x_2\)。
仙人掌
会了树之后,对于一般图我们显然也希望可以套用树的做法,圆方树就可以很好地帮我们把图转换成树的形态,所以我们不妨先考虑仙人掌的情况。
首先以 \(1\) 为根建出圆方树:
对于一个圆点,他的儿子是方点,这些方点的子树同样需要满足各自占领一段连续的区间,但是子树之间是可以任意排列的,所以递归处理之后套用树的做法即可。
对于一个方点,他代表了一个点双,由于是仙人掌,这里一个点双就是一个简单环。这个环上的点就不能随便乱排了,需要满足我们上面环的要求。但是这还不够,注意到这个方点存在一个父亲圆点,这个环上的其他圆点要么全都放在这个父亲之后,要么全都放在这个父亲之前,因此这个方点的儿子总共只有两种排列方法,一种正着放,一种反着放,取一个字典序最小的即可。
注:不管这些儿子圆点是放在父亲之前还是之后,这两种放法都是合法的,所以当前方点的决策并不依赖于父亲的决策。
一般连通图
现在一个点双并不一定是一个简单环了,但是题目保证了一定有解,所以可以想到这个点双应该不会很复杂,考虑分析一下这题中点双的性质:
结论一: 这个点双不能存在同胚于 \(K_4\) 的子图。也即这个点双是广义串并联图。
证:对于下面这个 \(K_4\),显然 \(1-2-3-4\) 和 \(1-2-4-3\) 这两个环不可能同时满足条件。
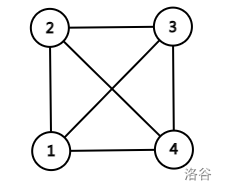
结论二: 这个点双不能存在同胚于下面这个图的子图。
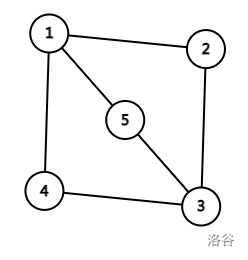
证:这个图有三个环 \(1-2-3-4\),\(1-2-3-5\),\(1-4-3-5\),我们枚举第一个环在排列上的摆放方式(共有 \(8\) 种,但是 \(1,3\) 放在开头的情况对称,\(2,4\) 放在开头的情况堆成,所以只枚举 \(4\) 种):
- \(1-2-3-4\):第二个环只能是 \(1-2-3-5\) 或者 \(5-1-2-3\),第三个环只能是 \(1-5-3-4\),显然不能同时合法。
- \(1-4-3-2\):第二个环只能是 \(1-5-3-2\),第三个环只能是 \(1-4-3-5\) 或者 \(5-1-4-3\),显然不能同时合法。
- \(2-3-4-1\),\(2-1-4-3\):同理,读者自证不难。
根据这两个结论可以知道这个点双形如一个圆,然后圆上有一些弦,任意两条弦不在除了顶点处相交。
所以这个点双的哈密尔顿回路存在且唯一,就是最外面的圆,这个回路同样需要满足上面简单环的限制。
我们只需要对每个点双求出哈密尔顿回路就可以套用仙人掌的做法了,一种经典求法是像广义串并联图那样每次缩二度点叠重边,然后在缩二度点的时候用链表维护哈密尔顿环,当然你也可以用 这篇题解 的做法。下面的代码里写的是前者。
一般图
我们先对每个连通块求出答案。
然后不难证明任意两个连通块在最终的答案序列上的区间要么不交,要么完全包含,即我们可以在某个连通块的答案序列中插入另一个连通块的完整的答案。
所以我们把所有连通块的答案按照第一个数排序,从第一个连通块开始填,当我即将要填的数大于下一个连通块的第一个数时,就跳到下一个连通块去做,做完了再继续填当前连通块的数。
复杂度 \(O(n)\) 或者 \(O(n\log n)\)。
code
贴一下用了一堆 STL 的巨大常数代码(但是跑进 \(2s\) 还是没问题的)。
点击查看代码
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define eb emplace_back
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5;inline int read(){int w=1,s=0;char c=getchar();for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());return w*s;
}
int c,T,n,m;
int dfn[N],low[N],st[N],top,l[N];
bool vis[N];
vector<int> G[N],E[N];
vector<vector<int> > res;
namespace Solve{int rt,num,cnt,fa[N],mn[N];int pre[N],nxt[N],deg[N],id[N];vector<int> res,dcc[N];set<int> S[N];set<PII> lst;void init(){for(int i=1;i<=cnt;i++) dcc[i].clear();top=num=cnt=0;res.clear();}void dfs0(int u,int fa){vis[u]=true;dfn[u]=low[u]=++num,st[++top]=u;for(int v:G[u]){if(v==fa) continue;if(!dfn[v]){dfs0(v,u),low[u]=min(low[u],low[v]);if(low[v]>=dfn[u]){int x; ++cnt,E[n+cnt].clear();do{x=st[top--];dcc[cnt].eb(x),E[n+cnt].eb(x),E[x].eb(n+cnt);}while(x!=v);dcc[cnt].eb(u),E[n+cnt].eb(u),E[u].eb(n+cnt);}} else low[u]=min(low[u],dfn[v]);}}void dfs1(int u,int Fa){fa[u]=Fa;if(Fa) E[u].erase(find(E[u].begin(),E[u].end(),Fa));for(int v:E[u]) dfs1(v,u);}void solve(){if(lst.size()==2){int u=(*lst.begin()).se,v=(*lst.rbegin()).se;nxt[u]=pre[u]=v,nxt[v]=pre[v]=u;return;}int u=(*lst.begin()).se,x,y; lst.erase(lst.begin());x=*S[u].begin(),y=*S[u].rbegin();S[x].erase(S[x].find(u)),S[y].erase(S[y].find(u));if(!S[x].count(y)) S[x].insert(y),S[y].insert(x);else{lst.erase({deg[x],x}),lst.erase({deg[y],y});deg[x]--,deg[y]--,lst.insert({deg[x],x}),lst.insert({deg[y],y});}solve();if(nxt[x]==y) nxt[x]=pre[y]=u,pre[u]=x,nxt[u]=y;else pre[x]=nxt[y]=u,nxt[u]=x,pre[u]=y;}void Get_Hamiltonloop(int c){lst.clear();for(int u:dcc[c]) id[u]=c;for(int u:dcc[c]){pre[u]=nxt[u]=u,deg[u]=0,S[u].clear(); for(int v:G[u]) if(id[u]==id[v]) S[u].insert(v),deg[u]++;lst.insert({deg[u],u});}solve();int x=nxt[fa[n+c]],t=fa[n+c];dcc[c].clear(),dcc[c].eb(t);while(x!=t) dcc[c].eb(x),x=nxt[x];}void dfs2(int u){if(!E[u].size()) return mn[u]=u,void();for(int v:E[u]) dfs2(v);if(u<=n){sort(E[u].begin(),E[u].end(),[&](int x,int y){return mn[x]<mn[y];});mn[u]=min(u,mn[E[u][0]]);}else{E[u].clear();int c=u-n;if(mn[dcc[c][1]]<mn[dcc[c].back()]) for(int i=1;i<dcc[c].size();i++) E[u].eb(dcc[c][i]);else for(int i=dcc[c].size()-1;i>=1;i--) E[u].eb(dcc[c][i]);mn[u]=mn[E[u][0]];}}void dfs3(int u){if(u>n) for(int v:E[u]) dfs3(v);else{bool flag=false;for(int v:E[u]){if(mn[v]>u&&!flag) res.eb(u),flag=true;dfs3(v);}if(!flag) res.eb(u);}}vector<int> work(){init();if(G[rt].size()==0){vis[rt]=true;return {rt};}dfs0(rt,0),dfs1(rt,0);for(int i=1;i<=cnt;i++) Get_Hamiltonloop(i);dfs2(rt),dfs3(rt);return res;}
}
void Init(){res.clear();for(int i=1;i<=n;i++) G[i].clear(),E[i].clear(),vis[i]=dfn[i]=low[i]=0;
}
void work(){Init();n=read(),m=read();for(int i=1;i<=m;i++){int u=read(),v=read();G[u].eb(v),G[v].eb(u);}int cnt=0,id=0;for(int i=1;i<=n;i++) if(!vis[i]) Solve::rt=i,res.push_back(Solve::work()),l[cnt++]=0;top=0;st[++top]=id++;while(top||id<cnt){if(top==0) st[++top]=id++;int i=st[top]; while(l[i]<res[i].size()&&(id==cnt||res[i][l[i]]<res[id][0])) printf("%d ",res[i][l[i]++]);if(l[i]<res[i].size()) st[++top]=id++;else top--;}puts("");
}
signed main(){c=read(),T=read();while(T--) work();return 0;
}
