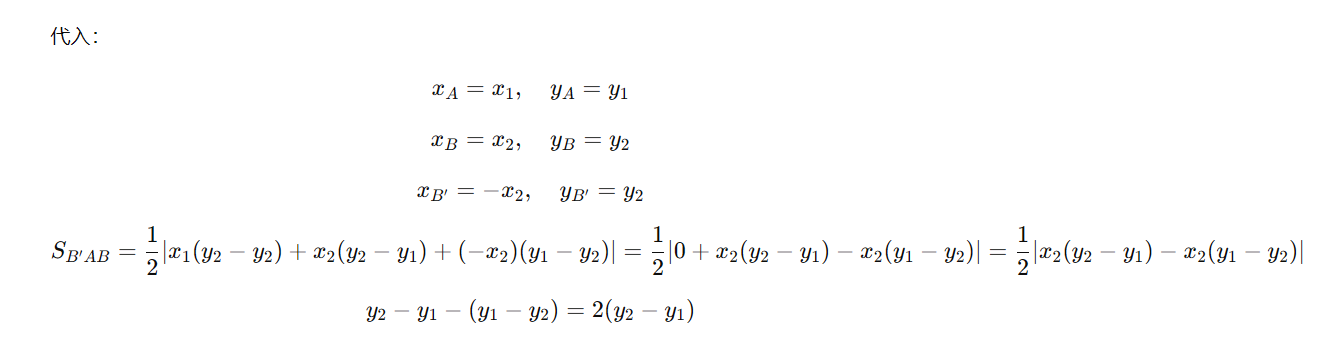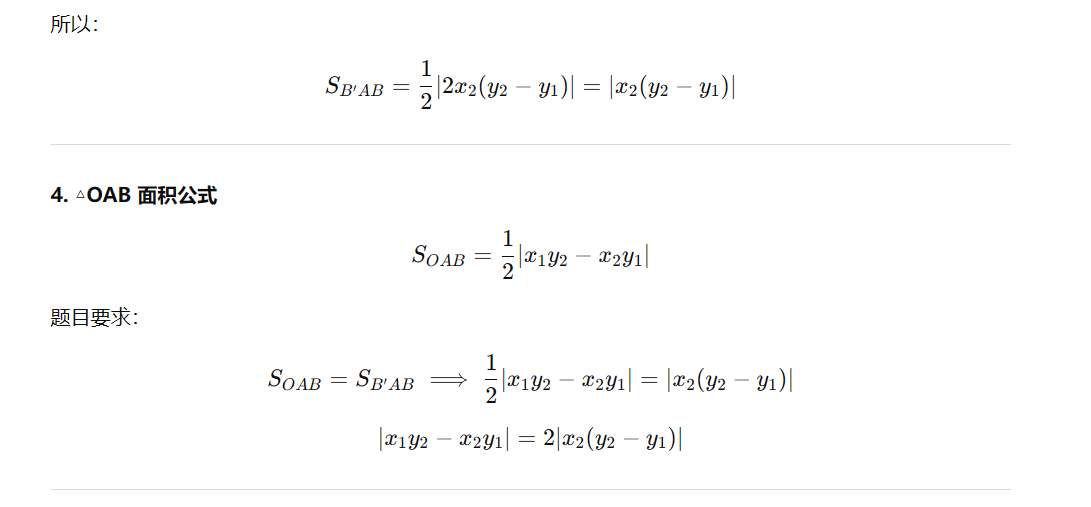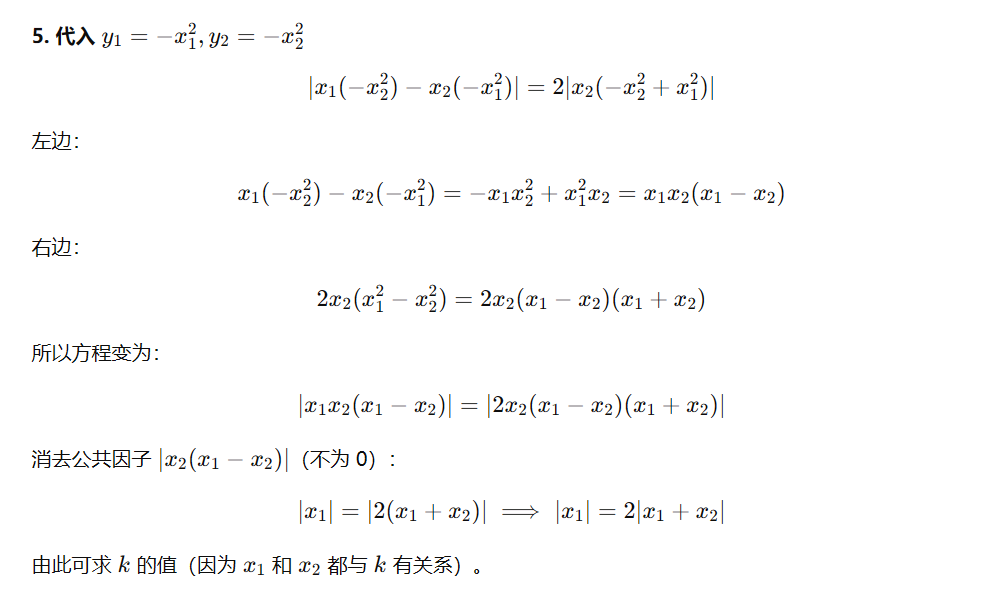你这张图片显示的是一道平面解析几何题,题目主要内容如下:
在平面直角坐标系 $xOy$ 中,有一条直线 $y = kx - 3$(其中 $k \neq 0$)和抛物线 $y = -x^2$,它们相交于两点 $A$ 和 $B$,并且点 $A$ 在点 $B$ 的左侧。题目还提到点 $B$ 关于 $y$ 轴的对称点为 $B'$。
题目分为三个部分:
-
求交点坐标
当 k = 2 时,求直线与抛物线的交点 A 和 B 的坐标。-
这一步通常需要把直线方程代入抛物线方程:
2x - 3 = -x^2 \implies x^2 + 2x - 3 = 0
然后解这个二次方程可以得到两个x 值,再求对应的 y值,得到交点的坐标。你在图片上写了A(-3, -9) 和 B(1, -1),这符合计算。
-
-
面积相等问题
连接 $O A$、$O B$、$A B'$ 和 $B B'$,题目要求 △$B'AB$ 的面积与 △$OAB$ 的面积相等,并求 $k$ 的值。-
这里需要先写出面积公式,可以用行列式法或者三角形面积公式:
$$
S = \frac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)|
$$ -
代入对应的点 $O(0,0)$、$A(x_1, y_1)$、$B(x_2, y_2)$ 和 $B'(x_3, y_3)$,列出方程求 $k$。
-
-
直线 AB' 是否经过固定点
探究直线 $AB'$ 是否经过某个固定点,如果是,则求该点坐标;如果不是,需要说明理由。- 分析思路:直线 $AB'$ 的斜率为 $\frac{y_B' - y_A}{x_B' - x_A}$,代入 $x_B' = -x_B$ 和对应的 $y$ 坐标,看是否能得到一个固定点(不随 $k$ 变化而变化的点)。
整道题的考点:
- 二次函数与直线交点的求法
- 对称点与几何变换
- 三角形面积计算
- 参数 $k$ 的讨论
- 分析直线经过固定点的问题
如果你需要,我可以帮你把第 2 和第 3 小题的详细计算过程也列出来,附上公式和步骤。这样整题就完全讲解清楚了。
你希望我帮你做吗?