AtCoder Grand Contest 015 - E - Mr.Aoki Incubator
思路解析
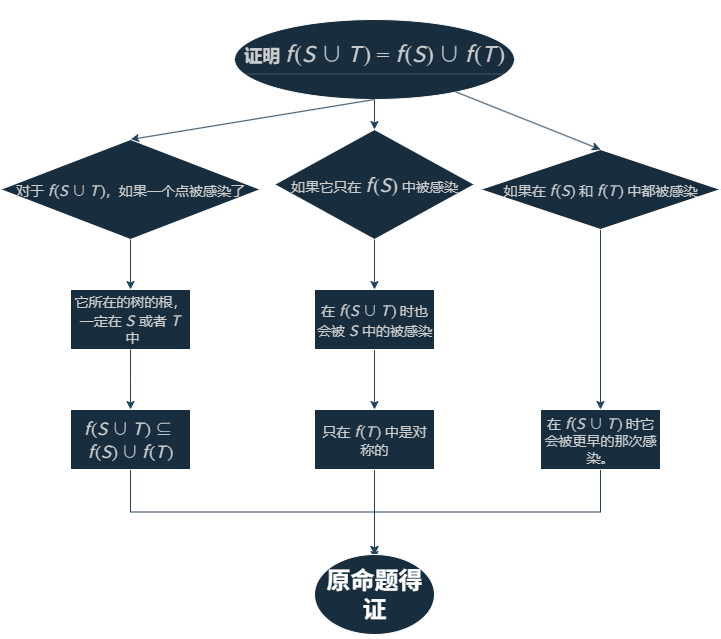
设 $ f(S) $ 为初始感染集合为 $ S $。
哪些人能够被最终感染呢?
我们考虑将每个人视作一个点,感染他的人视作它的父亲。
再观察 $ f({i}) $ 是什么,将每个人视作点 $ (V_i, X_i) $ 画在一维平面中,两个点会相遇且仅当两个点的连续斜率 \(< 0\),并且斜率绝对值越小相遇越早。
通过图我们可以发现最终被感染的点在横坐标上是一段区间,也就是 $ (V_i, X_i) $ 左上角矩形最靠右的,以及 $ (V_i, X_i) $ 右下角矩形最靠右的。
求出每个点会染色的区间 $ [l_i, r_i] $ 后,问题就变成了选出某些区间使得能够完全覆盖 $ [1, n] $,询问有多少种方案。令 $ f_r $ 为选出的区间恰好覆盖前 \(i\) 个点的方案数,每次转移枚举 $ r = i $ 的区间,按照左端点从小到大枚举,每次将 $ f_{l-1}, f_l, \ldots, f_r $ 加到 $ f_r $ 上即可。可以使用前缀和优化解决。
总的时间复杂度为 $ O(n \log n) $。
后记
奇技淫巧
似乎可以通过主席树优化拓扑排序的方法实现?
