图论常见结论及例题
常见结论
-
要在有向图上求一个最大点集,使得任意两个点 \((i,j)\) 之间至少存在一条路径(可以是从 \(i\) 到 \(j\) ,也可以反过来,这两种有一个就行),即求解最长路;
-
要求出连通图上的任意一棵生成树,只需要跑一遍 bfs ;
-
给出一棵树,要求添加尽可能多的边,使得其是二分图:对树进行二分染色,显然,相同颜色的点之间连边不会破坏二分图的性质,故可添加的最多的边数即为 \(cnt_{\tt Black}*cnt_{\tt White}-(n-1)\) ;
-
当一棵树可以被黑白染色时,所有染黑节点的度之和等于所有染白节点的度之和;
-
在竞赛图中,入度小的点,必定能到达出度小(入度大)的点 See 。
-
在竞赛图中,将所有点按入度从小到大排序,随后依次遍历,若对于某一点 \(i\) 满足前 \(i\) 个点的入度之和恰好等于 \(\left\lfloor \dfrac{n\cdot(n+1)}{2}\right\rfloor\) ,那么对于上一次满足这一条件的点 \(p\) ,\(p+1\) 到 \(i\) 点构成一个新的强连通分量 See 。
举例说明,设满足上方条件的点为 \(p_1,p_2\ (p_1+1<p_2)\) ,那么点 \(1\) 到 \(p_1\) 构成一个强连通分量、点 \(p_1+1\) 到 \(p_2\) 构成一个强连通分量。
-
选择图中最少数量的边删除,使得图不连通,即求最小割;如果是删除点,那么拆点后求最小割 See。
-
如果一张图是平面图,那么其边数一定小于等于 \(3n-6\) See 。
-
若一张有向完全图存在环,则一定存在三元环。
-
竞赛图三元环计数:See 。
-
有向图判是否存在环直接用 topsort;无向图判是否存在环直接用 dsu,也可以使用 topsort,条件变为
deg[i] <= 1时入队。
常见例题
杂
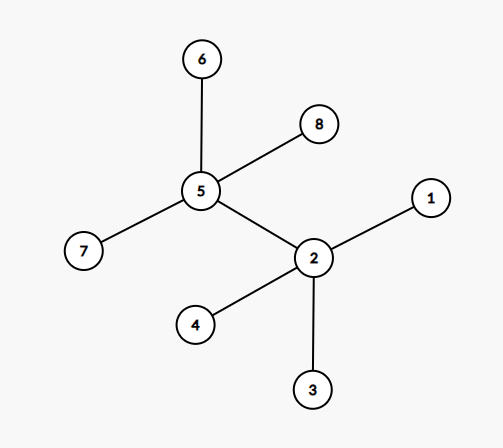
题意:给出一棵节点数为 \(2n\) 的树,要求将点分割为 \(n\) 个点对,使得点对的点之间的距离和最大。
可以转化为边上问题:对于每一条边,其被利用的次数即为 \(\min {\{ \text{其左边的点的数量}, \text{其右边的点的数量}\}}\) ,使用树形 \(\tt dp\) 计算一遍即可。如下图样例,答案为 \(10\) 。
vector<int> val(n + 1, 1);
int ans = 0;
function<void(int, int)> dfs = [&](int x, int fa) {for (auto y : ver[x]) {if (y == fa) continue;dfs(y, x);val[x] += val[y];ans += min(val[y], k - val[y]);}
};
dfs(1, 0);
cout << ans << endl;
题意:以哪些点为起点可以无限的在有向图上绕
概括一下这些点可以发现,一类是环上的点,另一类是可以到达环的点。建反图跑一遍 topsort 板子,根据容斥,未被移除的点都是答案 See 。
题意:添加最少的边,使得有向图变成一个 SCC
将原图的 SCC 缩点,统计缩点后的新图上入度为 \(0\) 和出度为 \(0\) 的点的数量 \(cnt_{\tt in}、cnt_{\tt out}\) ,答案即为 \(\max(cnt_{\tt in}, cnt_{\tt out})\) 。过程大致是先将一个出度为 \(0\) 的点和一个入度为 \(0\) 的点相连,剩下的点随便连 See 。
题意:添加最少的边,使得无向图变成一个 E-DCC
将原图的 E-DCC 缩点,统计缩点后的新图上入度为 \(1\) 的点(叶子结点)的数量 \(cnt\) ,答案即为 \(\left \lceil \frac{cnt}{2} \right \rceil\) 。过程大致是每次找两个叶子结点(但是还有一些条件限制)相连,若最后余下一个点随便连 See 。
题意:在树上找到一个最大的连通块,使得这个联通内点权和边权之和最大,输出这个值,数据中存在负数的情况。
使用 dfs 即可解决。
LL n, point[N];
LL ver[N], head[N], nex[N], tot; bool v[N];
map<pair<LL, LL>, LL> edge;
// void add(LL x, LL y) {}
void dfs(LL x) {for (LL i = head[x]; i; i = nex[i]) {LL y = ver[i];if (v[y]) continue;v[y] = true; dfs(y); v[y] = false;}for (LL i = head[x]; i; i = nex[i]) {LL y = ver[i];if (v[y]) continue;point[x] += max(point[y] + edge[{x, y}], 0LL);}
}
void Solve() {cin >> n;FOR(i, 1, n) cin >> point[i];FOR(i, 2, n) {LL x, y, w; cin >> x >> y >> w;edge[{x, y}] = edge[{y, x}] = w;add(x, y), add(y, x);}v[1] = true; dfs(1); LL ans = -MAX18;FOR(i, 1, n) ans = max(ans, point[i]);cout << ans << endl;
}
Prüfer 序列:凯莱公式
题意:给定 \(n\) 个顶点,可以构建出多少棵标记树?
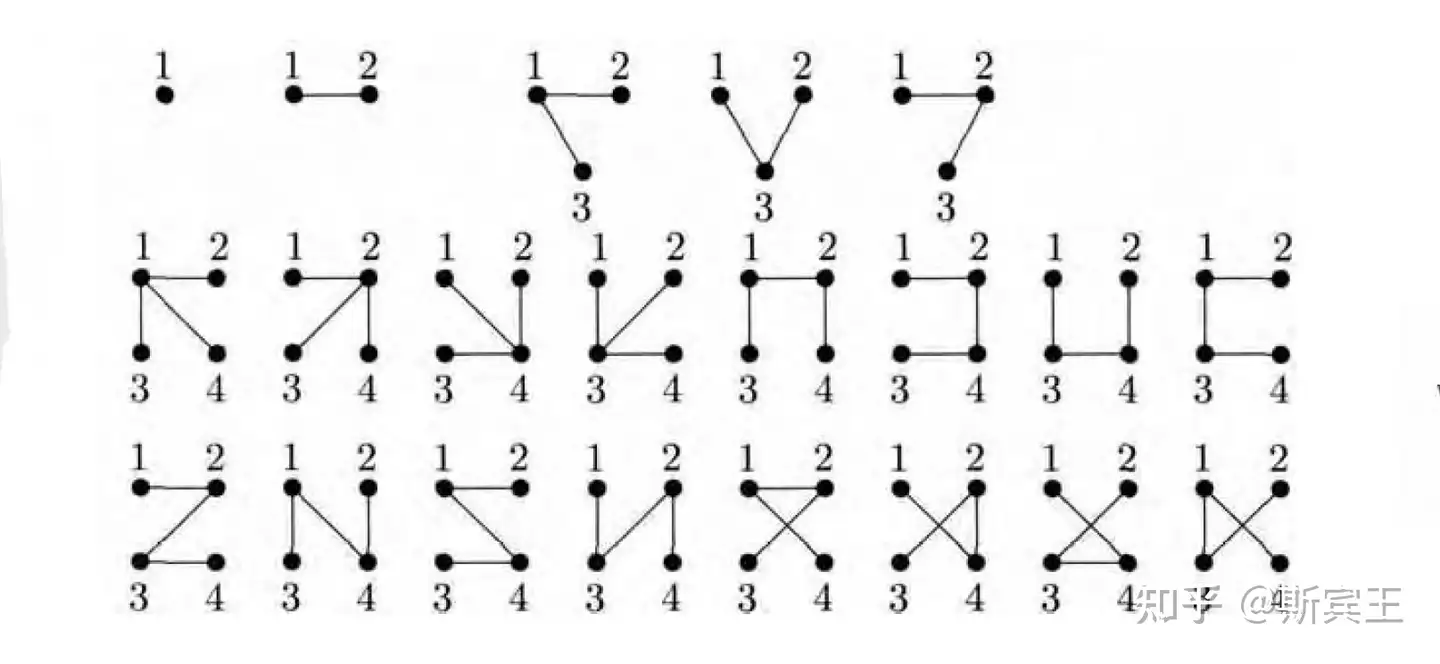
\(n\le 4\) 时的样例如上,通项公式为 \(n^{n-2}\) 。
Prüfer 序列
一个 \(n\) 个点 \(m\) 条边的带标号无向图有 \(k\) 个连通块。我们希望添加 \(k-1\) 条边使得整个图连通,求方案数量 See 。
设 \(s_i\) 表示每个连通块的数量,通项公式为 \(\displaystyle n^{k-2}\cdot\prod_{i=1}^ks_i\) ,当 \(k < 2\) 时答案为 \(1\) 。
单源最短/次短路计数
const int N = 2e5 + 7, M = 1e6 + 7;
int n, m, s, e; int d[N][2], v[N][2]; // 0 代表最短路, 1 代表次短路
Z num[N][2];void Clear() {for (int i = 1; i <= n; ++ i) h[i] = edge[i] = 0;tot = 0;for (int i = 1; i <= n; ++ i) num[i][0] = num[i][1] = v[i][0] = v[i][1] = 0;for (int i = 1; i <= n; ++ i) d[i][0] = d[i][1] = INF;
}int ver[M], ne[M], h[N], edge[M], tot;
void add(int x, int y, int w) {ver[++ tot] = y, ne[tot] = h[x], h[x] = tot;edge[tot] = w;
}void dji() {priority_queue<PIII, vector<PIII>, greater<PIII> > q; q.push({0, s, 0});num[s][0] = 1; d[s][0] = 0;while (!q.empty()) {auto [dis, x, type] = q.top(); q.pop();if (v[x][type]) continue; v[x][type] = 1;for (int i = h[x]; i; i = ne[i]) {int y = ver[i], w = dis + edge[i];if (d[y][0] > w) {d[y][1] = d[y][0], num[y][1] = num[y][0];// 如果找到新的最短路,将原有的最短路数据转化为次短路q.push({d[y][1], y, 1});d[y][0] = w, num[y][0] = num[x][type];q.push({d[y][0], y, 0});}else if (d[y][0] == w) num[y][0] += num[x][type];else if (d[y][1] > w) {d[y][1] = w, num[y][1] = num[x][type];q.push({d[y][1], y, 1});}else if (d[y][1] == w) num[y][1] += num[x][type];}}
}
void Solve() {cin >> n >> m >> s >> e;Clear(); //多组样例务必完全清空for (int i = 1; i <= m; ++ i) {int x, y, w; cin >> x >> y; w = 1;add(x, y, w), add(y, x, w);}dji();Z ans = num[e][0];if (d[e][1] == d[e][0] + 1) {ans += num[e][1]; // 只有在次短路满足条件时才计算(距离恰好比最短路大1)}cout << ans.val() << endl;
}
判定图中是否存在负环
使用 SPFA ,复杂度为 \(\mathcal{O}(KM)\) ,其中常数 \(K\) 相较裸的 SPFA 更高。
const int N = 1e5 + 7, M = 1e6 + 7;
int n, m;
int ver[M], ne[M], h[N], edge[M], tot;
int d[N], v[N], num[N];void add(int x, int y, int w) {ver[++ tot] = y, ne[tot] = h[x], h[x] = tot;edge[tot] = w;
}
bool spfa() {queue<int> q;for (int i = 1; i <= n; ++ i) q.push(i), v[i] = 1; //全部入队while(!q.empty()) {int x = q.front(); q.pop();v[x] = 0;for (int i = h[x]; i; i = ne[i]) {int y = ver[i];if(d[y] > d[x] + edge[i]) {num[y] = num[x] + 1;if (num[y] >= n) return true;d[y] = d[x] + edge[i];if(!v[y]) q.push(y), v[y] = 1;}}}return false;
}
int main() {cin >> n >> m;for (int i = 1; i <= m; ++ i) {int x, y, w; cin >> x >> y >> w;add(x, y, w);}if(spfa() == true) cout << "Yes" << endl;else cout << "No" << endl;
}
输出任意一个三元环
原题:给出一张有向完全图,输出任意一个三元环上的全部元素 See 。使用 dfs,复杂度 \(\mathcal O(N+M)\),可以扩展到非完全图和无向图。
int n;
cin >> n;
vector<vector<int>> a(n + 1, vector<int>(n + 1));
for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {char x;cin >> x;if (x == '1') a[i][j] = 1;}
}vector<int> vis(n + 1);
function<void(int, int)> dfs = [&](int x, int fa) {vis[x] = 1;for (int y = 1; y <= n; ++y) {if (a[x][y] == 0) continue;if (a[y][fa] == 1) {cout << fa << " " << x << " " << y;exit(0);}if (!vis[y]) dfs(y, x); // 这一步的if判断很关键}
};
for (int i = 1; i <= n; ++i) {if (!vis[i]) dfs(i, -1);
}
cout << -1;
带权最小环大小与计数
原题:给出一张有向带权图,求解图上最小环的长度、有多少个这样的最小环 See 。使用 floyd,复杂度为 \(\mathcal O(N^3)\) ,可以扩展到无向图。
LL Min = 1e18, ans = 0;
for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (dis[i][j] > dis[i][k] + dis[k][j]) {dis[i][j] = dis[i][k] + dis[k][j];cnt[i][j] = cnt[i][k] * cnt[k][j] % mod;} else if (dis[i][j] == dis[i][k] + dis[k][j]) {cnt[i][j] = (cnt[i][j] + cnt[i][k] * cnt[k][j] % mod) % mod;}}}for (int i = 1; i < k; i++) {if (a[k][i]) {if (a[k][i] + dis[i][k] < Min) {Min = a[k][i] + dis[i][k];ans = cnt[i][k];} else if (a[k][i] + dis[i][k] == Min) {ans = (ans + cnt[i][k]) % mod;}}}
}
最小环大小
原题:给出一张无向图,求解图上最小环的长度、有多少个这样的最小环 See 。使用 floyd,可以扩展到有向图。
int flody(int n) {for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {val[i][j] = dis[i][j]; // 记录最初的边权值}}int ans = 0x3f3f3f3f;for (int k = 1; k <= n; ++ k) {for (int i = 1; i < k; ++ i) { // 注意这里是没有等于号的for (int j = 1; j < i; ++ j) {ans = min(ans, dis[i][j] + val[i][k] + val[k][j]);}}for (int i = 1; i <= n; ++ i) { // 往下是标准的flodyfor (int j = 1; j <= n; ++ j) {dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);}}}return ans;
}
使用 bfs,复杂度为 \(\mathcal O(N^2)\) 。
auto bfs = [&] (int s) {queue<int> q; q.push(s);dis[s] = 0;fa[s] = -1;while (q.size()) {auto x = q.front(); q.pop();for (auto y : ver[x]) {if (y == fa[x]) continue;if (dis[y] == -1) {dis[y] = dis[x] + 1;fa[y] = x;q.push(y);}else ans = min(ans, dis[x] + dis[y] + 1);}}
};
for (int i = 1; i <= n; ++ i) {fill(dis + 1, dis + 1 + n, -1);bfs(i);
}
cout << ans;
本质不同简单环计数
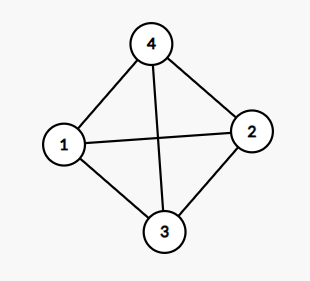
原题:给出一张无向图,输出简单环的数量 See 。注意这里环套环需要分别多次统计,下图答案应当为 \(7\)。使用状压 dp,复杂度为 \(\mathcal O(M\cdot2^N)\),可以扩展到有向图。
int n, m;
cin >> n >> m;
vector<vector<int>> G(n);
for (int i = 0; i < m; i++) {int u, v;cin >> u >> v;u--, v--;G[u].push_back(v);G[v].push_back(u);
}
vector<vector<LL>> dp(1 << n, vector<LL>(n));
for (int i = 0; i < n; i++) dp[1 << i][i] = 1;
LL ans = 0;
for (int st = 1; st < (1 << n); st++) {for (int u = 0; u < n; u++) {if (!dp[st][u]) continue;int start = st & -st;for (auto v : G[u]) {if ((1 << v) < start) continue;if ((1 << v) & st) {if ((1 << v) == start) {ans += dp[st][u];}} else {dp[st | (1 << v)][v] += dp[st][u];}}}
}
cout << (ans - m) / 2 << "\n";
输出任意一个非二元简单环
原题:给出一张无向图,不含自环与重边,输出任意一个简单环的大小以及其上面的全部元素 See 。注意输出的环的大小是随机的,不等价于最小环。
由于不含重边与自环,所以环的大小至少为 \(3\) ,使用 dfs 处理出 dfs 序,复杂度为 \(\mathcal O(N+M)\),可以扩展到有向图;如果有向图中二元环也允许计入答案,则需要删除下方标注行。
vector<int> dis(n + 1, -1), fa(n + 1);
auto dfs = [&](auto self, int x) -> void {for (auto y : ver[x]) {if (y == fa[x]) continue; // 二元环需删去该行if (dis[y] == -1) {dis[y] = dis[x] + 1;fa[y] = x;self(self, y);} else if (dis[y] < dis[x]) {cout << dis[x] - dis[y] + 1 << endl;int pre = x;cout << pre << " ";while (pre != y) {pre = fa[pre];cout << pre << " ";}cout << endl;exit(0);}}
};
for (int i = 1; i <= n; i++) {if (dis[i] == -1) {dis[i] = 0;dfs(dfs, 1);}
}
有向图环计数
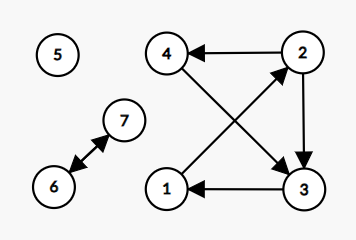
原题:给出一张有向图,输出环的数量。注意这里环套环仅需要计算一次,数据包括二元环和自环,下图例应当输出 \(3\) 个环。使用 dfs 染色法,复杂度为 \(\mathcal O(N+M)\)。
int ans = 0;
vector<int> vis(n + 1);
auto dfs = [&](auto self, int x) -> void {vis[x] = 1;for (auto y : ver[x]) {if (vis[y] == 0) {self(self, y);} else if (vis[y] == 1) {ans++;}}vis[x] = 2;
};
for (int i = 1; i <= n; i++) {if (!vis[i]) {dfs(dfs, i);}
}
cout << ans << endl;
输出有向图任意一个环
原题:给出一张有向图,输出任意一个环,数据包括二元环和自环。使用 dfs 染色法。
vector<int> dis(n + 1), vis(n + 1), fa(n + 1);
auto dfs = [&](auto self, int x) -> void {vis[x] = 1;for (auto y : ver[x]) {if (vis[y] == 0) {dis[y] = dis[x] + 1;fa[y] = x;self(self, y);} else if (vis[y] == 1) {cout << dis[x] - dis[y] + 1 << endl;int pre = x;cout << pre << " ";while (pre != y) {pre = fa[pre];cout << pre << " ";}cout << endl;exit(0);}}vis[x] = 2;
};
for (int i = 1; i <= n; i++) {if (!vis[i]) {dfs(dfs, i);}
}
判定带环图是否是平面图
原题:给定一个环以一些额外边,对于每一条额外边判定其位于环外还是环内,使得任意两条无重合顶点的额外边都不相交(即这张图构成平面图)See1, See2 。
使用 2-sat。考虑全部边都位于环内,那么“一条边完全包含另一条边”、“两条边完全没有交集”这两种情况都不会相交,可以直接跳过这两种情况的讨论。
signed main() {int n, m;cin >> n >> m;vector<pair<int, int>> in(m);for (int i = 0, x, y; i < m; i++) {cin >> x >> y;in[i] = minmax(x, y);}TwoSat sat(m);for (int i = 0; i < m; i++) {auto [s, e] = in[i];for (int j = i + 1; j < m; j++) {auto [S, E] = in[j];if (s < S && S < e && e < E || S < s && s < E && E < e) {sat.add(i, 0, j, 0);sat.add(i, 1, j, 1);}}}if (!sat.work()) {cout << "Impossible\n";return 0;}auto ans = sat.answer();for (auto it : ans) {cout << (it ? "out" : "in") << " ";}
}
