模拟赛
T1
枚举b3
n^2 处理出a_b1^a_b2=x的所有情况(满足b2<i)
然后枚举b4,计算答案
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){if(b==0) return 1;if(b==1) return a%p;int c=ksm(a,b/2,p);c=c*c%p;if(b%2==1) c=c*a%p;return c%p;
}
inline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}
int a[5005];
int mm[2000005];
signed main()
{//freopen("filename.in", "r", stdin);//freopen("filename.out", "w", stdout);int n=read();for(int i=1;i<=n;i++){a[i]=read();} int ans=0;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){int zh=a[i]^a[j];ans+=mm[zh];}for(int j=1;j<i;j++){int zh=a[i]^a[j];mm[zh]++;}}cout<<ans<<'\n';return 0;
}
T2
首先若一个数两列全相同,一定为0
然后将其删去
注意若一个数高位全不同,这个数一定是p-1
进而发现所有数不同的高位数量都不同
根据这个算答案即可
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<bits/stdc++.h>
#define int long long
#define jiaa(a,b) {a+=b;if(a>=MOD) a-=MOD;}
#define jian(a,b) {a-=b;if(a<0) a+=MOD;}
using namespace std;
int ksm(int a,int b,int p){if(b==0) return 1;if(b==1) return a%p;int c=ksm(a,b/2,p);c=c*c%p;if(b%2==1) c=c*a%p;return c%p;
}
inline int read()
{int x=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}
int a[2005][4005],vis[2005];
signed main()
{//freopen("filename.in", "r", stdin);//freopen("filename.out", "w", stdout);int p=read();for(int i=0;i<p;i++){int sum=0;for(int j=0;j<p;j++) vis[j]=0;for(int j=0;j<2*p;j++){a[i][j]=read();if(j%2==0){if(!vis[a[i][j]]) sum++;vis[a[i][j]]=1;}}
// cout<<sum<<'\n';if(sum==1){sum=0;for(int j=0;j<p;j++) vis[j]=0;for(int j=0;j<2*p;j++){if(j%2==1){if(!vis[a[i][j]]) sum++;vis[a[i][j]]=1;}}if(sum==1) cout<<0<<' ';else cout<<1<<' ';}else cout<<sum<<' ';}cout<<'\n';return 0;
}
T3
分治
对每个点求出到mid,mid+1的最短路
对每一行,求出当这一行最优时对哪些点产生贡献
这是一个二维数点,树状数组解决
递归时注意到最短路不一定在区间内部
所以需要处理区间内每个点到区间端点的最短路
容易发现改变的部分就是刚刚求出的到mid,mid+1最短路
注意求最短路可以dp(拐点较少,<=4),不要dij,多一个log
T4
先考虑k=1时dp
dpi,j,0/1,0/1,表示1~i插入完成最终序列有j个连续段,是否已经占据最终序列的开头,是否已经占据最终序列的结尾

数学
数论
素数
逆元
Wilson 定理
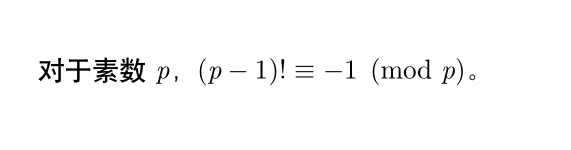
证明考虑乘法逆元
欧几里得算法
(exgcd)

中国剩余定理
扩展:对每个方程的模数质因数分解,对每个质数分别考虑check
转化成普通剩余定理
exgcd即可
积性函数
容易发现积性函数f(1)=1
完全积性函数,省去互素条件
埃氏筛
线性筛
思路可拓展求积性函数前缀和
整数分块
阶
离散对数
莫比乌斯反演+欧拉反演
组合数学
插板法
例题

考虑乘积的组合意义
插板后对每个段加一个小球
再次进行插板
共插2p+1个板
容斥原理
min-max反演
二项式反演
斯特林数

错排
1.递推
2.容斥
卡特兰数
转化在数轴上
格路计数
两条线?
不合法容斥系数=0
prufer序列
一棵n个点有标号的无根树有n^(n-2)个
生成prufer序列:

还原树:

线性代数
矩阵加/乘
矩阵乘组合意义:i->j的方案数
向量
矩阵快速幂
高斯消元
主元和自由元
线性空间
线性相关
秩
称一组线性空间的秩,为其最大的内部线性无关子空间
可以使用高斯消元求解
对于一组解,我们称之为线性基
正交线性基
对于每一个主元,保证只有一个数是包含它的
行列式

发现相邻行之间加减不影响最终结果
高斯消元变成阶梯矩阵
易求答案
