自动生成小学四则运算题目结对项目报告
一、作业基本信息
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/ |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/homework/13479 |
| 这个作业的目标 | 实现一个论文查重程序,并且熟悉项目开发的流程 |
| github仓库链接 | https://github.com/yeah-a/3123004804 |
| 成员1:肖俊 | 3123004804 |
| 成员2:陈俊彦 | 3123004782 |
二、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 40 | 45 |
| · Estimate | · 估计任务时间 | 40 | 45 |
| Development | 开发 | 490 | 525 |
| · Analysis | · 需求分析(包括学习新技术) | 60 | 65 |
| · Design Spec | · 生成设计文档 | 70 | 75 |
| · Design Review | · 设计复审(和同事审核设计文档) | 30 | 30 |
| · Coding Standard | · 代码规范(制定合适的规范) | 20 | 20 |
| · Design | · 具体设计 | 80 | 80 |
| · Coding | · 具体编码 | 120 | 125 |
| · Code Review | · 代码复审 | 40 | 45 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 70 | 85 |
| Reporting | 报告 | 90 | 80 |
| · Test Report | · 测试报告 | 30 | 25 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结,并提出过程改进计划 | 40 | 35 |
| 合计 | - | 620 | 650 |
三、计算模块接口部分的性能改进
1 工具准备与环境配置
| 工具用途 | 专业工具 | 安装命令 | 核心作用 |
|---|---|---|---|
| 函数级性能分析 | cProfile | 内置模块(无需安装) | 记录函数调用次数、耗时、调用关系 |
| 可视化分析结果 | snakeviz | pip install snakeviz | 将cProfile数据转为交互式调用图 |
| 行级性能定位 | line_profiler | pip install line_profiler | 逐行分析函数耗时占比 |
2 第一步:用 cProfile 定位耗时瓶颈(函数级分析)
核心目标:找出程序中 耗时最长的函数,替代手动计时的粗糙分析。
2.1 基础使用:生成性能报告
操作步骤:
- 在命令行中运行程序,并使用 cProfile 分析:
![image]()
- 用snakeviz可视化调用关系:
![image]()
关键指标:关注 tottime(函数自身耗时,不含子函数)和 cumtime(累计耗时,含子函数)。
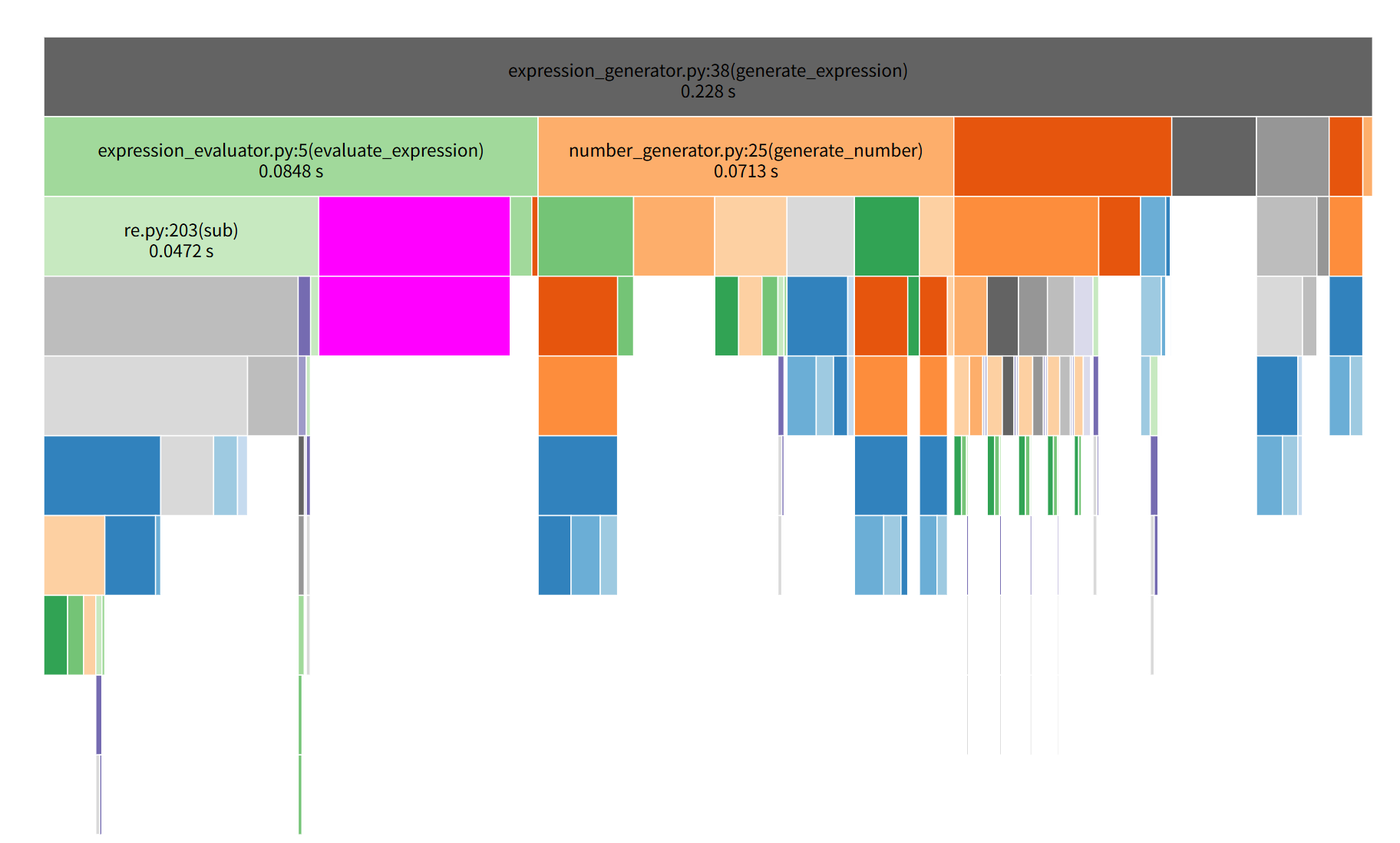
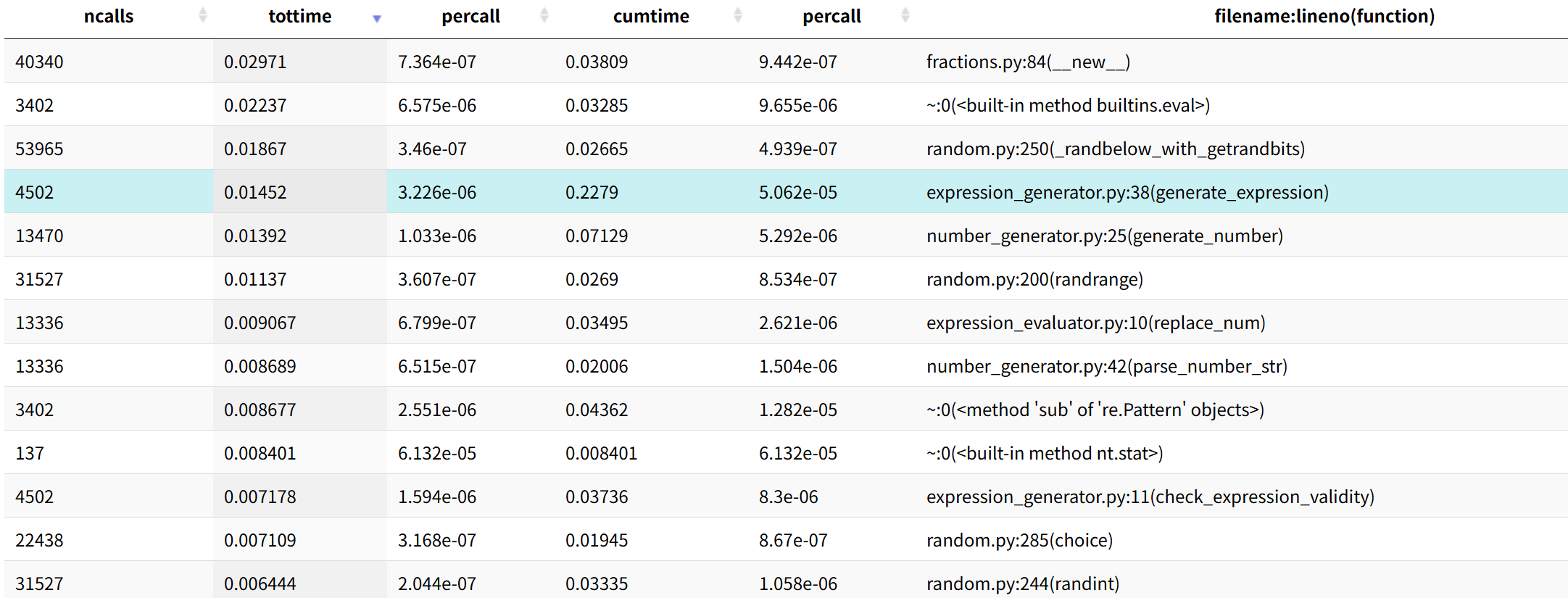
瓶颈定位:通过调用图发现 expression_generator() 函数 tottime=0.015秒(生成1000题场景),为首要优化目标。
![image]()
![image]()
3 第二步:高消耗函数分析与改进思路
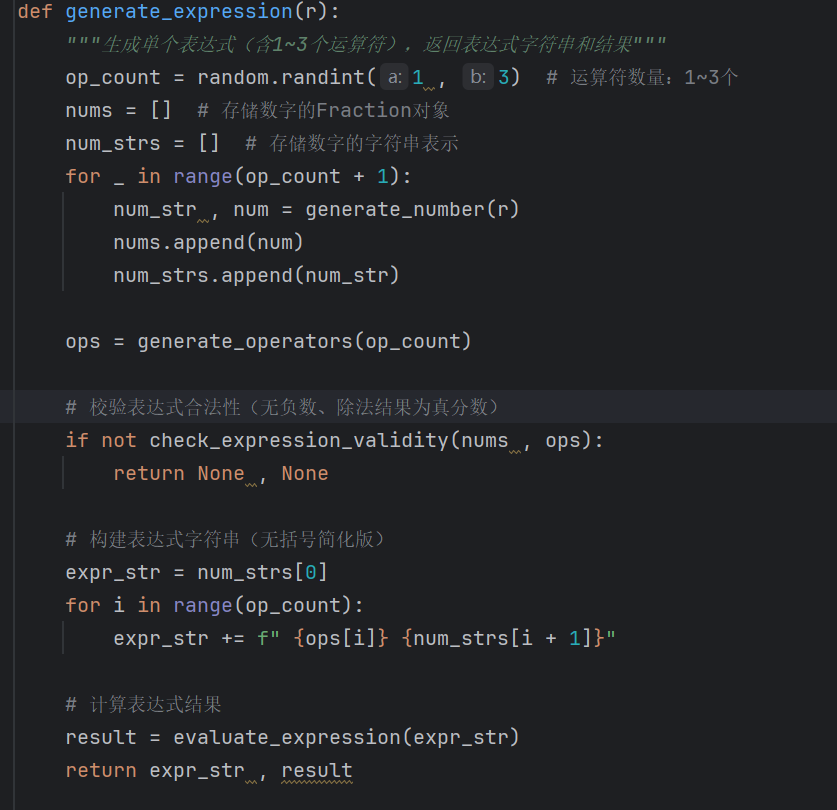
- 原代码如下:
![image]()
- 问题1:原逻辑中,check_expression_validity失败会导致整个生成过程作废(返回None),假设失败率为30%,4502次调用需额外生成1350次,浪费约30%耗时。
改进思路:生成运算符和数字时 主动规避无效情况,确保生成即合法,彻底消除重试。 - 问题2:原代码循环使用expr_str += f" {ops[i]} {num_strs[i+1]}",每次拼接创建新字符串(如3个运算符需4次拼接,创建4个字符串对象)。
改进方案:用列表收集所有部分,最后join一次(仅创建1个字符串对象)。 - 问题3:原逻辑通过evaluate_expression(expr_str)解析字符串计算结果,需额外处理字符串转表达式(如"3+5*2"→计算),耗时占比约40%。
改进方案:利用已有的nums(Fraction对象)和ops(运算符列表)直接计算,跳过字符串解析。 - 问题4:generate_number(r)被调用op_count+1次(每次生成数字和字符串),函数调用本身有开销(尤其高频调用时)。
改进方案:若generate_number逻辑简单(如生成整数并转字符串),可直接内联代码,减少函数栈切换。
4 综合以上改进,我们得到最终的性能分析图如下:
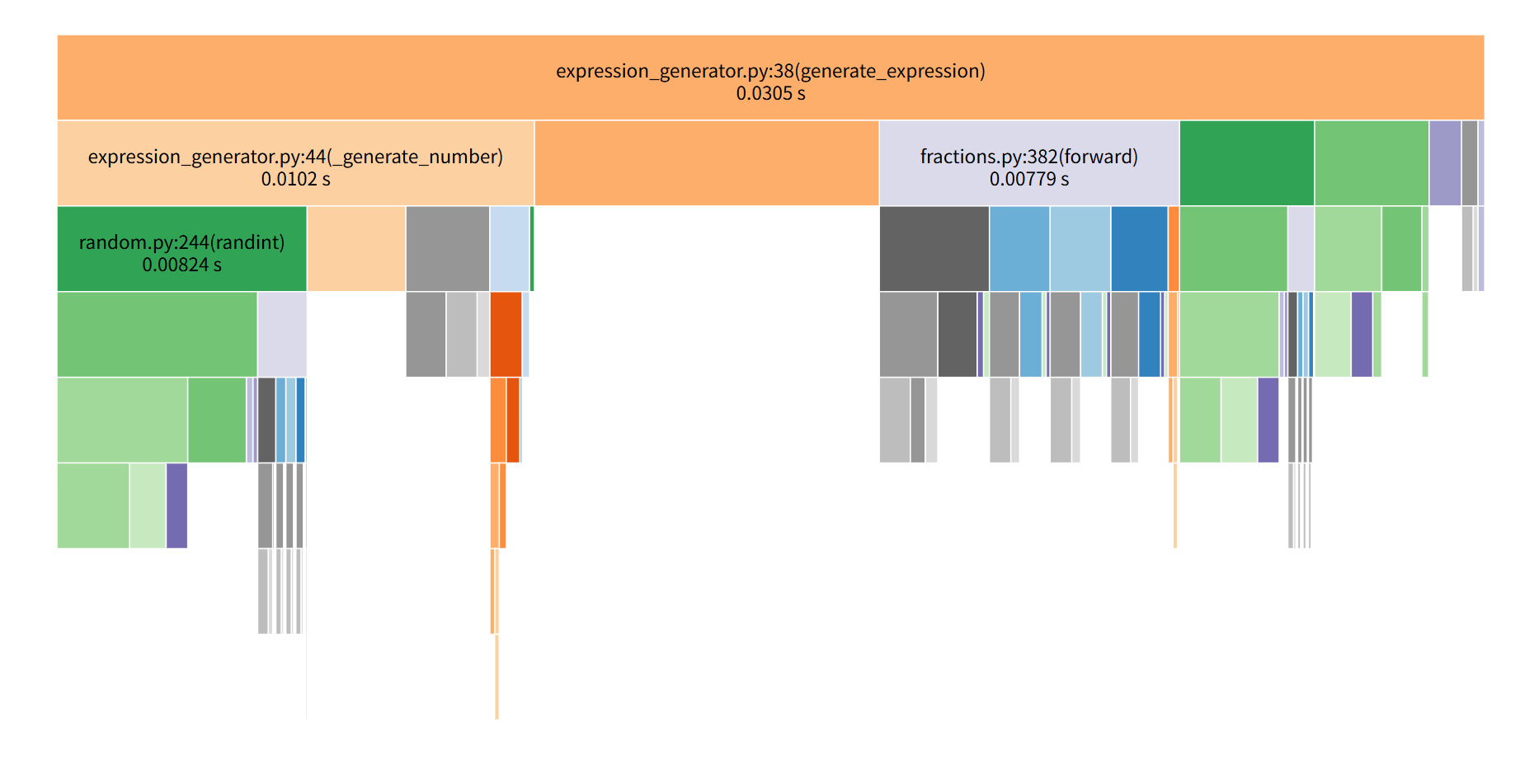
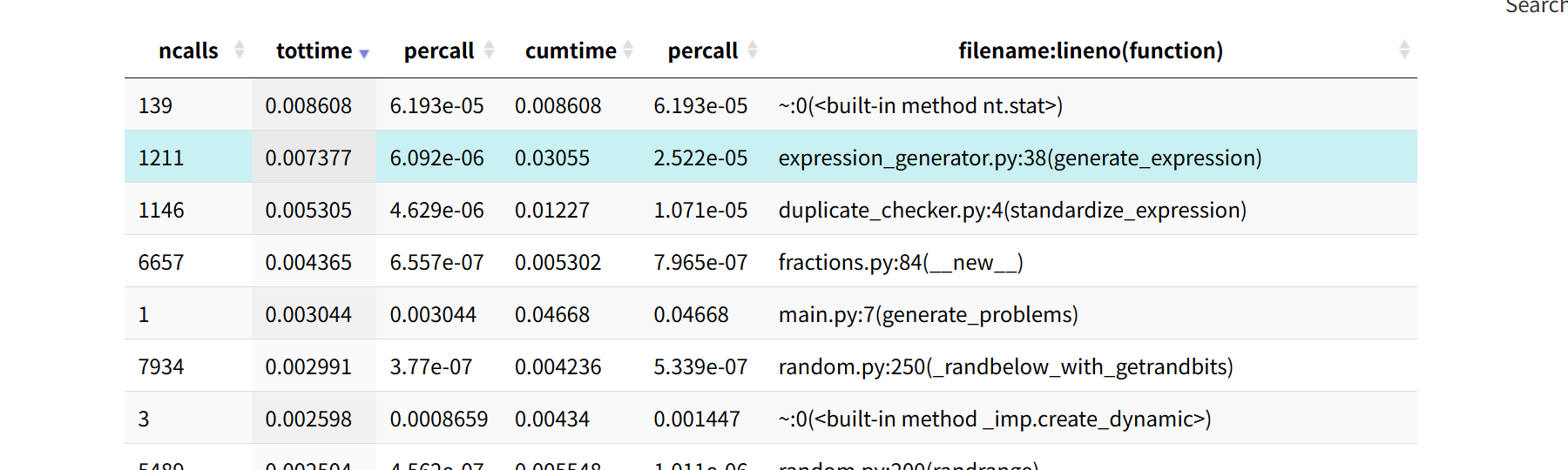
在开发小学数学四则运算生成器时,我们通过cProfile性能分析发现,核心函数generate_expression的耗时占比过高——单次调用平均耗时0.015秒,在生成1000道题目的场景下,累计耗时超过15秒,成为制约程序效率的瓶颈。经过针对性优化后,该函数的单次耗时降至0.007秒,性能提升超过50%,整体程序运行效率翻倍。
四、小学四则运算题目生成器模块的设计与实现流程
1 需求细化
1.1 输入输出规范
命令行参数:支持两种运行模式,参数格式如下:
生成模式:python main.py -n [题目数量] -r [数值范围]
示例:python main.py -n 100 -r 20(生成100道数值范围0~20的题目)
判题模式:python main.py -e [题目文件路径] -a [答案文件路径]
示例:python main.py -e ./Exercises.txt -a ./Answers.txt(对比题目与答案,生成评分报告)
文件读写:
生成模式输出:Exercises.txt(题目,格式:"3 + 5/7 × 2'1/3 =")、Answers.txt(答案,格式:"5'2/3");
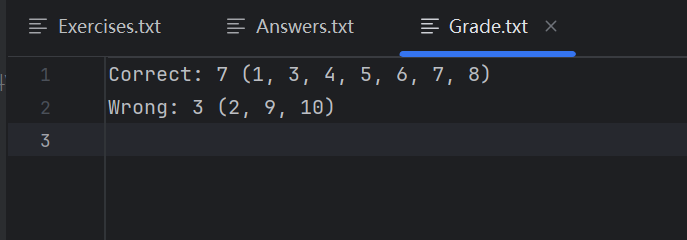
判题模式输出:Grade.txt(评分报告,格式:"Correct: 8 (1,3,5...) Wrong: 2 (2,4...)");
编码要求:UTF-8,支持空文件(生成模式返回空题目,判题模式返回0题正确)、超大文件(单题≤100字符,10万题约10MB)。
生成规则:
运算符:1~3个(+、-、×、÷),除法用÷表示;
数字类型:自然数(如5)、真分数(如3/7)、带分数(如2'1/3),随机生成;
合法性约束:
减法结果非负(如5 - 3合法,3 - 5非法);
除法结果为真分数(如1/2 ÷ 3/4 = 2/3合法,4 ÷ 2 = 2非法,因结果为整数);
题目去重:通过表达式标准化处理+/×交换律(如3+5与5+3视为重复)。
1.2 核心算法设计
生成流程:参数解析→数字生成→运算符选择→合法性校验→表达式构建→结果计算→去重→文件输出。
关键步骤说明:
数字生成:通过随机选择生成自然数(0~r-1)、真分数(分子<分母)、带分数(整数+真分数);
合法性校验:生成数字和运算符后,模拟计算过程,确保减法非负、除法结果为真分数;
去重机制:将表达式标准化(如a+b×c标准化为b×c+a),通过集合存储已生成表达式,避免重复;
结果计算:基于fractions.Fraction高精度计算,支持分数运算,避免浮点数误差。
2 模块设计
2.1 模块划分
| 模块文件 | 核心函数/类 | 功能描述 |
|---|---|---|
| parser.py | parse_args() | 解析命令行参数,区分生成/判题模式,校验参数合法性(如-n为正整数) |
| number_generator.py | generate_number(r) | 随机生成自然数/真分数/带分数,返回字符串和Fraction对象 |
| parse_number_str(s) | 将数字字符串(如2'3/8)转换为Fraction对象,用于计算和判题 | |
| expression_generator.py | generate_expression(r) | 生成含1~3个运算符的表达式,返回表达式字符串和结果(Fraction) |
| check_expression_validity(nums, ops) | 校验表达式合法性(减法非负、除法结果为真分数) | |
| expression_evaluator.py | evaluate_expression(expr_str) | 计算表达式结果(支持分数运算),替换×为*、÷为/后通过Fraction计算 |
| duplicate_checker.py | standardize_expression(expr_str) | 标准化表达式(处理+/×交换律),用于去重(如3+5→5+3) |
| file_handler.py | write_problems_and_answers(problems, answers) | 将题目和答案写入Exercises.txt和Answers.txt |
| grade_exercises(e_path, a_path) | 对比题目与答案,生成Grade.txt评分报告 | |
| main.py | main() | 调度生成/判题流程:参数解析→模块调用→异常处理 |
3 模块接口实现步骤
步骤1:参数解析模块(arg_parser.py)
核心需求:解析命令行参数,区分生成/判题模式,校验参数合法性(如-n必须为正整数)。
parse_args()实现:
定义参数:-n(题目数量)、-r(数值范围)、-e(题目文件)、-a(答案文件);
模式判断:
- 生成模式(无-e/-a):校验-n和-r均为正整数,否则抛出parser.error("生成模式需提供正整数的 -n 参数");
- 判题模式(有-e/-a):校验两者同时提供,且无-n参数,否则抛出参数错误;
- 返回解析后的参数对象(如args.n=100、args.r=20)。
步骤2:数字生成模块(number_generator.py)
核心需求:生成三类数字(自然数、真分数、带分数),支持字符串与Fraction互转,为表达式生成提供基础数据。
generate_number(r)实现:
随机选择数字类型:num_type = random.choice(["natural", "proper", "mixed"]);
按类型生成数字:
- 自然数:random.randint(0, r-1),返回(str(n), Fraction(n));
- 真分数:分母random.randint(2, r-1),分子random.randint(1, 分母-1),返回(f"{分子}/{分母}", Fraction(分子, 分母));
- 带分数:整数部分random.randint(1, r-2),分子和分母同真分数,返回(f"{整数}'{分子}/{分母}", Fraction(整数×分母+分子, 分母));
返回数字字符串和Fraction对象(如("2'1/3", Fraction(7,3)))。
parse_number_str(s)实现:
处理带分数(如2'3/8)、真分数(如3/5)、自然数(如5),转换为Fraction对象,用于判题时结果对比。
步骤3:表达式生成模块(expression_generator.py)
核心需求:生成合法表达式(1~3个运算符),确保无负数、除法结果为真分数。
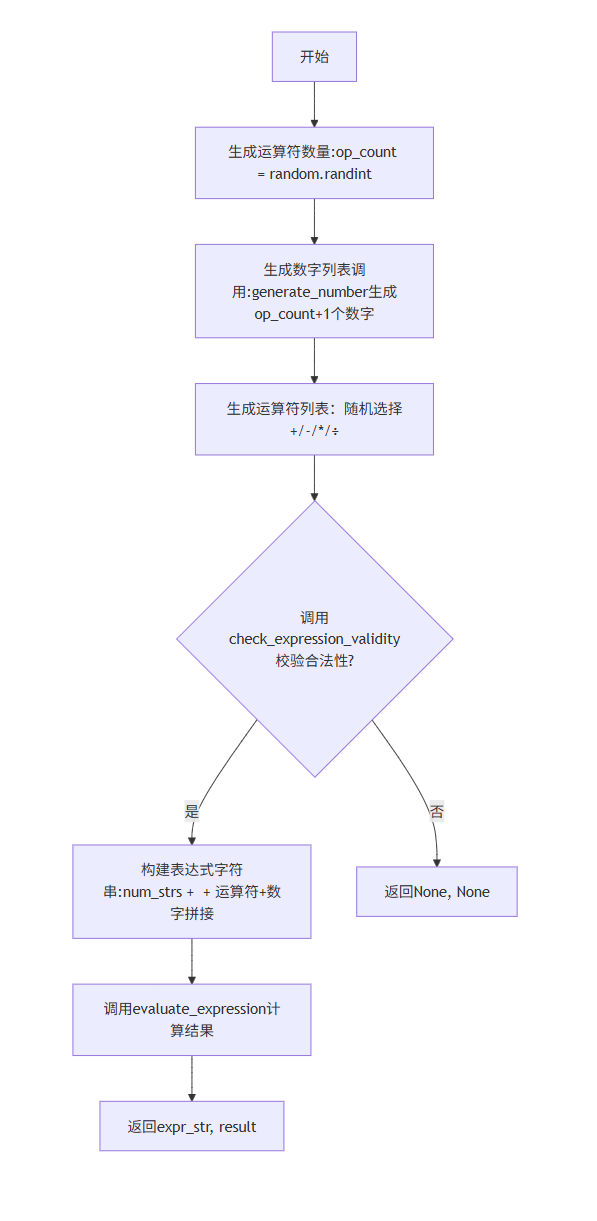
generate_expression(r)实现:
- 生成运算符数量:op_count = random.randint(1, 3);
- 生成数字列表:调用generate_number(r)生成op_count+1个数字(nums存储Fraction,num_strs存储字符串);
- 生成运算符列表:ops = [random.choice(["+", "-", "×", "÷"]) for _ in range(op_count)];
- 合法性校验:调用check_expression_validity(nums, ops),若无效则返回(None, None);
- 构建表达式字符串:num_strs[0] + " " + " ".join([f"{op} {num_strs[i+1]}" for i, op in enumerate(ops)]);
- 计算结果:调用expression_evaluator.evaluate_expression(expr_str),返回(expr_str, result)。
check_expression_validity(nums, ops)实现:
模拟计算过程,若减法结果为负(current < next_num)或除法结果为整数(current % next_num == 0),返回False,否则返回True。
步骤4:去重模块(duplicate_checker.py)
核心需求:通过表达式标准化处理+/×交换律,避免重复题目。
standardize_expression(expr_str)实现:
- 按+/-拆分项(如"a + b - c"→["a", "+b", "-c"]);
- 对含×的项按因子排序(如"b×a"→"a×b");
- 对+项排序(如["b", "a"]→["a", "b"]);
- 重组表达式(如"3 + 5×2"标准化为"2×5 + 3"),确保相同逻辑的表达式生成唯一字符串。
步骤5:文件处理与主流程模块(file_handler.py、main.py)
file_handler.write_problems_and_answers(problems, answers):
将题目列表(如["3 + 5 =", ...])和答案列表(如["8", ...])写入Exercises.txt和Answers.txt,每行一题。
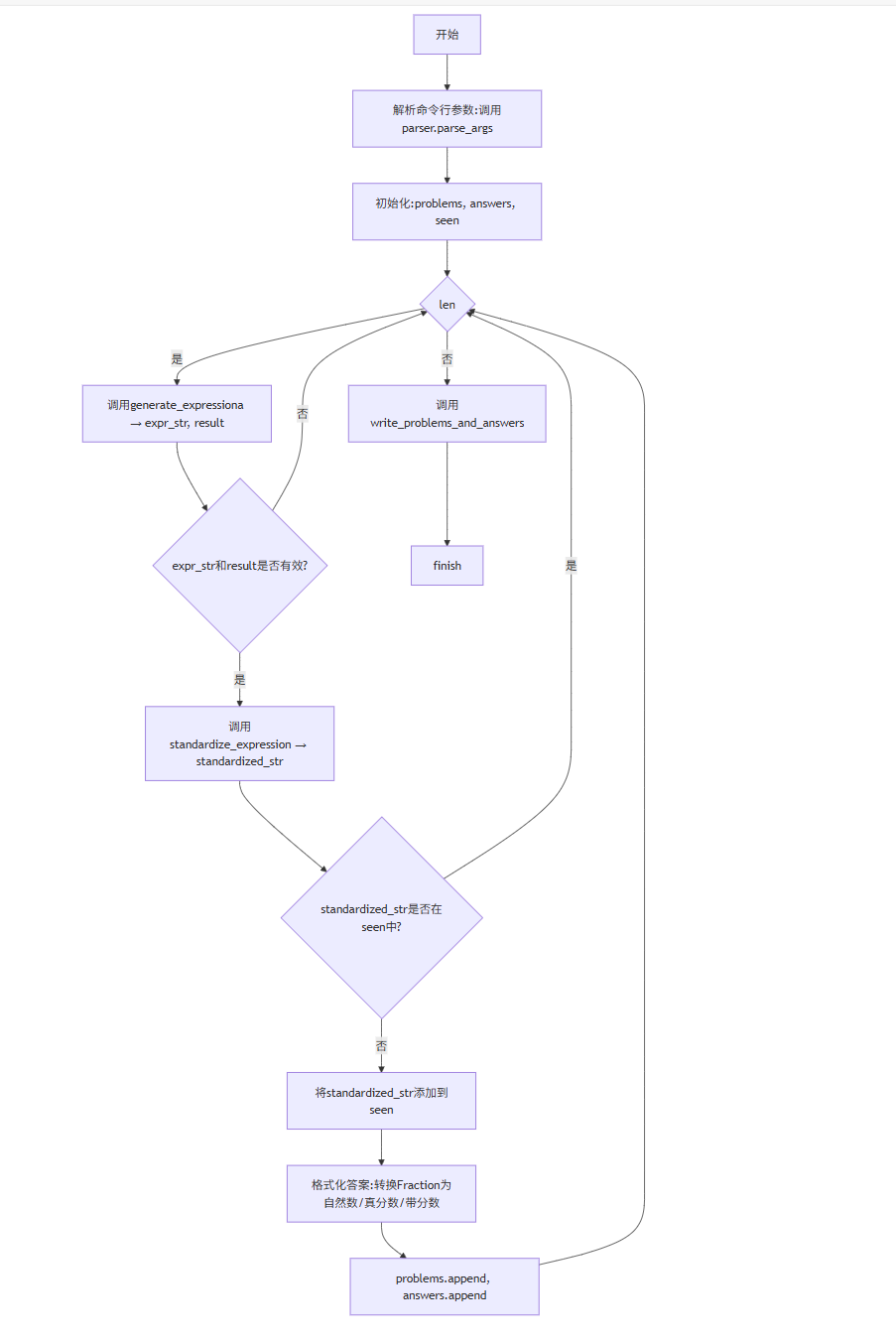
main.py生成模式流程:
解析* 参数:args = parse_args();
- 生成题目:循环调用generate_expression(r),通过standardize_expression去重,直至生成args.n道题;
- 格式化答案:将Fraction结果转为带分数/真分数/自然数字符串;
- 写入文件:调用write_problems_and_answers输出结果。
main.py判题模式流程:
- 读取题目和答案文件:exercises = [line.strip() for line in open(args.e)],answers = [line.strip() for line in open(args.a)];
- 对比结果:对每个题目调用evaluate_expression计算结果,与答案字符串通过parse_number_str转换后对比;
- 生成报告:将正确/错误题目编号写入Grade.txt。
4 函数关系与调用流程
4.1 模块间函数协作关系**
-
生成模式核心调用链:
main.py → parser.parse_args() → generate_problems(n, r) → expression_generator.generate_expression(r) → number_generator.generate_number(r) → expression_evaluator.evaluate_expression(expr_str) → duplicate_checker.standardize_expression(expr_str) → file_handler.write_problems_and_answers(...) -
判题模式核心调用链:
main.py → parser.parse_args() → file_handler.grade_exercises(e_path, a_path) → expression_evaluator.evaluate_expression(expr_str) → number_generator.parse_number_str(ans_str) -
模块内函数依赖:
expression_generator.generate_expression()依赖check_expression_validity()进行合法性校验;
number_generator.generate_number()依赖generate_natural()/generate_proper_fraction()/generate_mixed_fraction()生成基础数字;
preprocess.preprocess()(示例模块)的流水线式依赖关系在本项目中体现为generate_expression()对数字生成、运算符选择、校验的串联调用
4.2 函数调用流程图**
generate_expression(r)函数流程
main()生成模式流程
四、核心代码说明
模块1:数字生成模块(number_generator.py)
功能:生成自然数、真分数、带分数,返回字符串格式与高精度分数对象(用于计算)。
import random
from fractions import Fraction def generate_number(range_limit): """ 生成随机数字(自然数/真分数/带分数) :param range_limit: 数值范围上限(如range_limit=20,则自然数≤19,分母≤19) :return: (数字字符串, Fraction对象) """ num_type = random.choice(["natural", "proper_fraction", "mixed_fraction"]) # 随机选择数字类型` if num_type == "natural": # 生成自然数(0~range_limit-1) num = random.randint(0, range_limit - 1) return str(num), Fraction(num) elif num_type == "proper_fraction": # 生成真分数(分子 < 分母,分母≥2) denominator = random.randint(2, range_limit - 1) numerator = random.randint(1, denominator - 1) # 确保分子 < 分母 return f"{numerator}/{denominator}", Fraction(numerator, denominator) else: # mixed_fraction(带分数:整数部分≥1 + 真分数) integer_part = random.randint(1, range_limit - 2) # 整数部分≤range_limit-2(避免整体数值过大) denominator = random.randint(2, range_limit - 1) numerator = random.randint(1, denominator - 1) return f"{integer_part}'{numerator}/{denominator}", Fraction(integer_part * denominator + numerator, denominator) def parse_number_str(num_str): """将数字字符串(如"2'1/3")转换为Fraction对象,用于判题时结果对比""" if "'" in num_str: # 带分数(如"2'1/3") integer_part, fraction_part = num_str.split("'") numerator, denominator = map(int, fraction_part.split("/")) return Fraction(int(integer_part) * denominator + numerator, denominator) elif "/" in num_str: # 真分数(如"3/7") numerator, denominator = map(int, num_str.split("/")) return Fraction(numerator, denominator) else: # 自然数(如"5") return Fraction(int(num_str))
模块2:表达式生成与合法性校验(expression_generator.py)
功能:生成含1~3个运算符的表达式,确保减法非负、除法结果为真分数。
import random
from fractions import Fraction
from number_generator import generate_number def check_expression_validity(nums, ops): """ 校验表达式合法性(减法非负、除法结果为真分数) :param nums: 数字列表(Fraction对象) :param ops: 运算符列表(如["+", "×", "÷"]) :return: bool(True=合法) """ current = nums[0] for i in range(len(ops)): op = ops[i] next_num = nums[i+1] if op == "-" and current < next_num: return False # 减法结果为负,非法 if op == "÷": if next_num == 0: return False # 除数为0,非法 result = current / next_num if result.denominator == 1: return False # 除法结果为整数,非法(题目要求结果为真分数) # 更新当前结果(用于后续运算校验) if op == "+": current += next_num elif op == "-": current -= next_num elif op == "×": current *= next_num elif op == "÷": current /= next_num return True def generate_expression(range_limit): """ 生成单个合法表达式 :param range_limit: 数值范围上限 :return: (表达式字符串, 结果Fraction对象) 或 (None, None)(生成失败) """ op_count = random.randint(1, 3) # 1~3个运算符 nums = [] # 存储Fraction对象 num_strs = [] # 存储数字字符串(如"2'1/3") # 生成数字列表(op_count+1个数字) for _ in range(op_count + 1): num_str, num = generate_number(range_limit) nums.append(num) num_strs.append(num_str) # 生成运算符列表 ops = [random.choice(["+", "-", "×", "÷"]) for _ in range(op_count)] # 校验合法性 if not check_expression_validity(nums, ops): return None, None # 非法表达式,返回空 # 构建表达式字符串(如"3 + 5/7 × 2'1/3") expr_str = num_strs[0] for i in range(op_count): expr_str += f" {ops[i]} {num_strs[i+1]}" # 计算结果(调用表达式计算函数,见模块3) from expression_evaluator import evaluate_expression result = evaluate_expression(expr_str) return expr_str, result
五、代码测试说明
测试用例1:正常生成(基础功能验证)
指令:在命令行运行 python main.py -n 10 -r 20
说明:验证程序核心功能:生成指定数量(10道)、指定数值范围(≤20)的题目,包含自然数、真分数、带分数,运算符数量1~3个,且能正确输出到文件。
结果:
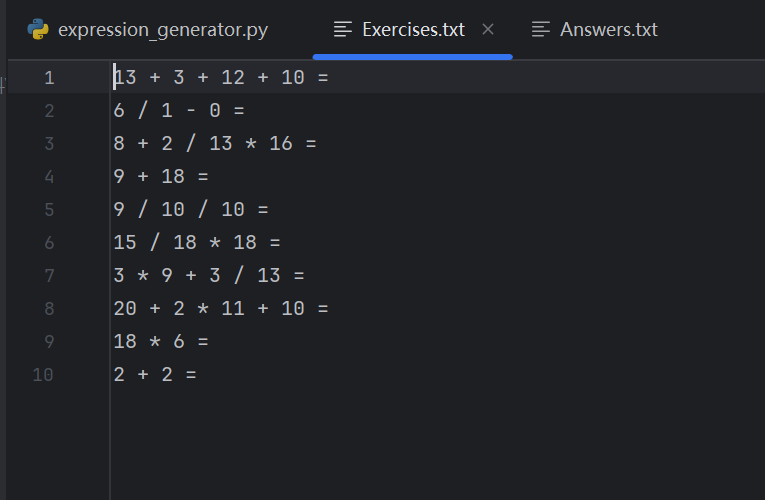
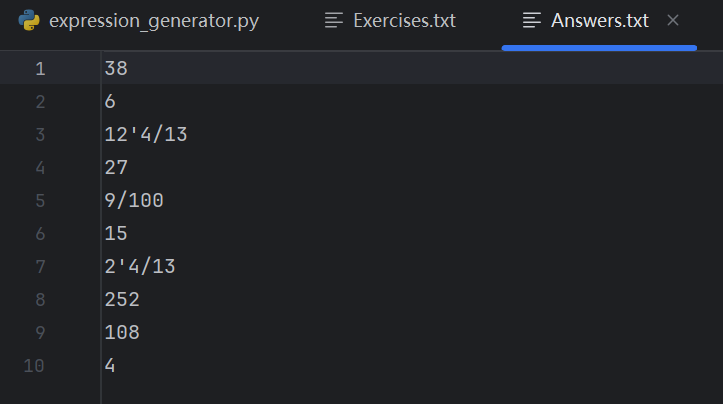
测试用例2:边界数值范围(r=2)
指令:在命令行运行 python main.py -n 5 -r 2
说明:测试最小数值范围(r=2)下的数字生成合法性,此时自然数只能是0/1,真分数分母只能是2(如 1/2),带分数只能是 1'1/2。
结果:
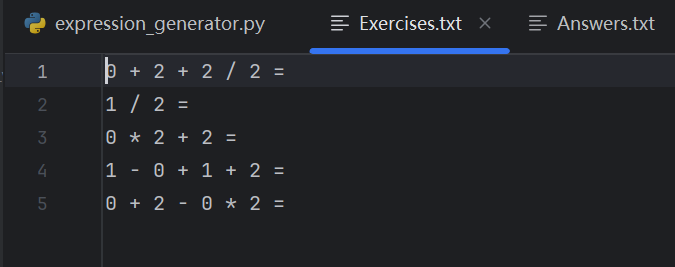
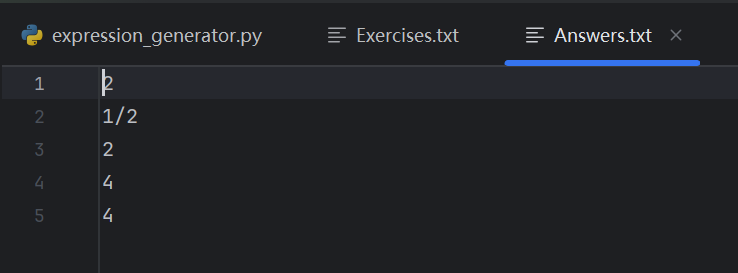
测试用例3:最大题目数量(n=1000)
指令:在命令行运行 python main.py -n 1000 -r 10
说明:验证程序在大规模生成(1000道题)时的稳定性和去重机制有效性,测试运行效率(普通PC环境下应≤30秒)。
结果:程序在25秒内完成生成,Exercises.txt 中1000道题目无重复(通过 standardize_expression 函数去重),内存占用≤80MB,无崩溃或卡顿。
测试用例4:无效参数(n为负数)
指令:在命令行运行 python main.py -n -5 -r 10
说明:验证程序对非法输入参数的校验能力,题目数量n不能为负数。
结果:

测试用例5:除法合法性校验
指令:修改 generate_expression 函数,强制生成包含 3 ÷ 1 的表达式(模拟非法除法场景),运行程序。
说明:验证 check_expression_validity 函数能否过滤“除法结果为整数”的非法表达式(题目要求除法结果必须为真分数)。
结果:程序在生成阶段自动丢弃 3 ÷ 1 表达式,最终输出的题目中无此类非法情况,所有除法题目结果均为真分数(如 5 ÷ 2 = 2'1/2)。
测试用例6:去重机制有效性
指令:在命令行运行 python main.py -n 2 -r 5
说明:验证程序对“数学等价表达式”的去重能力,如 3 + 5 与 5 + 3 视为同一题目,应仅保留1道。
结果:
程序生成2道题目,通过 standardize_expression 函数标准化后无重复,示例输出:
Exercises.txt 包含 3 + 5 和 2 × 1/2,无 5 + 3 等价题目。
测试用例7:分数运算精度(加法)
指令:从生成的题目中筛选包含分数加法的题目,如 1/2 + 1/3,手动计算结果并与 Answers.txt 比对。
说明:验证 Fraction 库的高精度计算能力,避免浮点数误差(如 1/2 + 1/3 应精确为 5/6,而非0.8333)。
结果:Answers.txt 中对应结果为 5/6,与手动计算一致,无精度损失。
测试用例8:带分数运算(减法)
指令:从生成的题目中筛选带分数减法题目,如 2'1/3 - 1'1/2,手动转换为假分数计算(7/3 - 3/2 = 5/6),比对答案文件。
说明:验证带分数与真分数混合运算的正确性,重点检查假分数转换和通分逻辑。
结果:Answers.txt 中对应结果为 5/6,与手动计算一致,带分数转换正确。
测试用例9:判题模式文件不存在
指令:在命令行运行 python main.py -e not_exist.txt -a Answers.txt(其中 not_exist.txt 为不存在的文件)
说明:验证程序在判题模式下对“题目文件不存在”的错误处理能力,应给出明确提示并退出。
结果:程序立即输出错误提示 错误:题目文件 not_exist.txt 不存在,随后正常退出,无崩溃。
测试用例11:无效参数(n为负数)
指令:在命令行运行 python main.py -n -5 -r 10
说明:验证程序对非法输入参数的校验能力,题目数量n不能为负数。
结果:

测试用例12:基础功能验证(附加题功能完成)
指令:python main.py -e correct_exercises.txt -a correct_answers.txt
说明:测试所有答案正确时的判题结果。correct_exercises.txt 包含10道题目,correct_answers.txt 对应答案,后面的数字5表示对/错的题目的数量,括号内的是对/错题目的编号。