| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/ |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/homework/13479 |
| 姓名 | 学号 | GitHub 项目地址 |
|---|---|---|
| 曾子轩 | 3123004763 | https://github.com/paulzzx/project2_AG/tree/main/project2 |
| 刘瑞康 | 3123004753 | https://github.com/paulzzx/project2_AG/tree/main/project2 |
一、PSP表
| PSP2.1 阶段 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 40 |
| Estimate | 估计这个任务需要多少时间 | 10 | 20 |
| Development | 开发 | 240 | 360 |
| Analysis | 需求分析(包括学习新技术) | 30 | 30 |
| Design Spec | 生成设计文档 | 30 | 40 |
| Design Review | 设计复审(和同事审核设计文档) | 30 | 20 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 20 | 10 |
| Design | 具体设计 | 60 | 90 |
| Coding | 具体编码 | 30 | 40 |
| Code Review | 代码复审 | 20 | 30 |
| Test | 测试(自我测试,修改代码,提交修改) | 20 | 40 |
| Reporting | 报告 | 40 | 60 |
| Test Report | 测试报告 | 20 | 40 |
| Size Measurement | 计算工作量 | 30 | 40 |
| Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 20 | 30 |
| 合计 | 350 | 570 |
二、系统设计与实现
1.代码组织
ArithmeticGenerator/
|——src/
│ |—— rational.py # 数字处理,假分数转换为带分数/字符串和数字的相互转换
│ |—— expr_ast.py # 用AST表示表达式,节点为运算符,叶子为数字。包括表达式的计算和打印
│ |—— canon.py # 递归处理表达式,返回规范化结果用于查重
│ |—— generator.py # 随机生成表达式、校验与批量产出
│ |—— checker.py # 将字符串转化为表达式计算,与答案比对,输出正确和错误的题数/题号
│ |—— cli.py # 命令行接口:参数解析与主流程
│ |—— __ init __.py
|——tests/ # pytest 单元与集成测试
│ |—— test_rational.py
│ |—— test_expr_ast.py
│ |—— test_generator.py
│ |—— ...
2.关键函数调用
—— 生成过程 ——
run # 解析命令行参数
-> generate_to_files(n: int, r: int, max_ops: int = 3) # 生成表达式和答案并写入文件
-> generate_exercises(n: int, R: int, max_ops: int = 3) -> Tuple[List[str], List[str]] # 批量生成表达式
-> random_expr(R: int, max_ops: int) # 生成随机表达式
-> canon_key(e: Expr) # 规范化表达式,返回key用于查重
-> pretty(e: Expr) -> str # 将查重后表达式转换为字符串
-> answer_of(e: Expr) -> str # 计算表达式结果并转换为字符串
—— 批改/判分过程(单题)——
run # 解析命令行参数
->check_to_grade(exercises_path: str, user_answers_path: str) # 检查并把结果写入grade
-> check_answers(exercises_path: str, user_answers_path: str, grade_out: str) -> Tuple[int, int, List[int]] # 读取题目计算并和答案比对
->_eval_from_text(expr_str: str) -> Fraction / parse_value(s: str) -> Fraction #计算题目得到答案 /将答案字符串转化为数值进行比对
3.代码说明
rational.parse_value
先匹配带分数、再匹配普通分数,避免歧义
解析失败统一 ValueError
Fraction保证分数精度,正则化确保格式
_INT_RE = re.compile(r"^\d+$")
_FRAC_RE = re.compile(r"^(\d+)/(\d+)$")
_MIXED_RE = re.compile(r"^(\d+)'(\d+)/(\d+)$")def parse_value(s: str) -> Fraction:if s is None:raise ValueError("empty")s = s.strip().replace("’", "'")# 整数if _INT_RE.fullmatch(s):return Fraction(int(s), 1)# 带分数 a'b/cm = _MIXED_RE.fullmatch(s)if m:a, b, c = (int(m.group(1)), int(m.group(2)), int(m.group(3)))if c == 0:print('分母为0')raise ValueError("denominator is zero")if b >= c:# 带分数部分必须 0 <= b < cprint('带分数部分必须 0 <= b < c')raise ValueError("improper mixed fraction")return Fraction(a * c + b, c)# 真/假分数 p/qm = _FRAC_RE.fullmatch(s)if m:p, q = int(m.group(1)), int(m.group(2))if q == 0:print('分母为0')raise ValueError("denominator is zero")return Fraction(p, q)raise ValueError(f"invalid value: {s!r}")
expr_ast.pretty
递归地遍历表达式树,将算术表达式格式化成字符串
如果节点是数字(Num),直接格式化输出
如果是二元运算(BinOp),递归打印左右子树,并根据运算符优先级决定是否加括号,最后用相应符号(+ - × ÷)连接左右表达式,生成完整的算式字符串
def pretty(e: Expr) -> str:if isinstance(e, Num):return format_value(e.value)assert isinstance(e, BinOp)l_txt = pretty(e.left)r_txt = pretty(e.right)if _need_paren(e.op, e.left, is_right_child=False):l_txt = f"({l_txt})"if _need_paren(e.op, e.right, is_right_child=True):r_txt = f"({r_txt})"op_txt = {Op.ADD: "+", Op.SUB: "-", Op.MUL: "×", Op.DIV: "÷"}[e.op]return f"{l_txt} {op_txt} {r_txt}"
canon.canon_key
等价只允许在 +/× 当前结点交换左右子树
去重确定性强,配合生成器防止重复题目
def canon_key(e: Expr) -> Key:"""构建表达式规范key,使等价表达式变成同一键。"""# 叶子:固定成最简分数的 (num, den)if isinstance(e, Num):fr = Fraction(e.value) # 规整(含 0 -> 0/1)return ('N', fr.numerator, fr.denominator)# 递归到子树,构子键assert isinstance(e, BinOp)kl = canon_key(e.left)kr = canon_key(e.right)# 仅对 ADD/MUL 在“本结点”做交换(排序);SUB/DIV 保持顺序if e.op in (Op.ADD, Op.MUL):a, b = (kl, kr) if kl <= kr else (kr, kl)return ('B', e.op.name, (a, b))else: # Op.SUB / Op.DIVreturn ('B', e.op.name, (kl, kr))
generator.generate_exercises
去重:canon_key + set,只允许“本结点交换”等价
非负约束:SUB 用“换位减”避免注入多余 + 节点,保证 ≤ max_ops
非整数除法:DIV 分母为 0 就修复;若整除则扰动分母,确保结果分数
输出题面时用 leaf_formatter=format_value → 假分数叶子显示为带分数,可读性更强
def generate_exercises(n: int, R: int, max_ops: int = 3) -> Tuple[List[str], List[str]]:"""生成恰好 n 道题(1≤n≤10000),操作数范围 [0, R](R≥1)。约束:- 任意子表达式与最终结果非负- 出现 DIV 时,该子表达式结果为分数- 运算符数 ≤ max_ops- 去重:基于 canon_key(仅局部交换)返回:(exercises, answers)exercises[i] = f"{i+1}. <expr_str> ="answers[i] = f"{i+1}. <value_str>"不能达成 n 条 → 抛 AGGenerateError。"""# 参数校验if not (1 <= n <= 10000):print('n must be in [1, 10000]')raise ValueError("n must be in [1, 10000]")if R < 1:print('R must be >= 1')raise ValueError("R must be >= 1")if max_ops < 1:print('max_ops must be >= 1')raise ValueError("max_ops must be >= 1")seen = set()exercises: List[str] = []answers: List[str] = []idx = 1# 防死循环的硬上限HARD_LIMIT = max(1000, 20 * n)attempts = 0while len(exercises) < n:if attempts >= HARD_LIMIT:print('cannot reach the required number of unique exercises')raise AGGenerateError("cannot reach the required number of unique exercises")attempts += 1# 生成随机算式try:e = random_expr(R, max_ops)except AGGenerateError:print('random generator failed')raise#验证合法性if not is_valid_expr(e):continue#验证唯一性k = canon_key(e)if k in seen:continueseen.add(k)expr_str = pretty(e) # 题面:最小括号val_str = answer_of(e) # 答案:冻结格式exercises.append(f"{idx}. {expr_str} =")answers.append( f"{idx}. {val_str}")idx += 1return exercises, answers
checker.check_answers
容错批改:用户答案 ValueError(空值、分母缺失、分母为 0、乱写)都判错,流程继续并生成成绩
成绩文件固定两行、ID 升序,便于对比与自动化检查
def check_answers(exercises_path: str, user_answers_path: str, grade_out: str) -> Tuple[int, int, List[int]]:"""严格按题号对齐批改:- 读题面/答案(依赖 io_utils 的强格式)- 题面经 _eval_from_text 得到标准答案(Fraction)- 用户答案用 rational.parse_value 解析(支持 '’')- 比较 Fraction 是否相等- 输出成绩文件两行固定格式,并返回 (correct_count, wrong_count, wrong_ids)"""# 1) 读取并做题号集合校验(格式不对由 io_utils 直接抛 ValueError)ex_pairs = io_utils.read_exercises(exercises_path) # [(id, "<expr>"), ...]an_pairs = io_utils.read_answers(user_answers_path) # [(id, "<value>"), ...]ex_map: Dict[int, str] = dict(ex_pairs)an_map: Dict[int, str] = dict(an_pairs)ex_ids = set(ex_map.keys())an_ids = set(an_map.keys())if ex_ids != an_ids:print('题号不匹配')raise ValueError("mismatched ids between exercises and answers")# 2) 批改(严格按升序题号对齐)correct_ids: List[int] = []wrong_ids: List[int] = []for i in sorted(ex_ids):gold = _eval_from_text(ex_map[i]) # 标准答案 Fractiontry:pred = parse_value(an_map[i]) # 用户答案 -> Fractionexcept ValueError as e:# 只特判“分母为 0”,判错但不中断if "denominator is zero" in str(e):wrong_ids.append(i)continue# 其它解析错误仍视为致命(保持原有行为/退出码 4)except ValueError:# 任何“结构不正确/解析失败”的答案都当作答错,但不中断wrong_ids.append(i)continueraiseif gold == pred:correct_ids.append(i)else:wrong_ids.append(i)# 3) 写成绩文件(两行固定格式;ID 升序)def _fmt(ids: List[int]) -> str:return "(" + ", ".join(map(str, ids)) + ")" if ids else "()"correct_ids.sort()wrong_ids.sort()with open(grade_out, "w", encoding="utf-8") as f:f.write(f"Correct: {len(correct_ids)} {_fmt(correct_ids)}\n")f.write(f"Wrong: {len(wrong_ids)} {_fmt(wrong_ids)}\n")return len(correct_ids), len(wrong_ids), wrong_ids
三、运行测试
test_rational.py
@pytest.mark.parametrize("fr, expect_a, expect_rem",[(F(0, 1), 0, F(0, 1)), # 0 -> (0, 0/1)(F(1, 2), 0, F(1, 2)), # 真分数 -> (0, 本身)(F(7, 3), 2, F(1, 3)), # 假分数 -> 带分数(F(5, 1), 5, F(0, 1)), # 整数 -> (a, 0/1)],
)
def test_to_mixed_basic(fr, expect_a, expect_rem):a, rem = to_mixed(fr)assert a == expect_aassert rem == expect_remdef test_to_mixed_invariants():"""不变量:返回 (a, b/c),且 0 <= b < c,c>0;整数时余数固定为 0/1。"""for fr in [F(0, 1), F(1, 2), F(7, 3), F(99, 10), F(5, 1)]:a, rem = to_mixed(fr)assert rem.denominator > 0# 允许 0/1if rem == 0:assert rem == F(0, 1)else:assert 0 <= rem.numerator < rem.denominator@pytest.mark.parametrize("fr, expect",[(F(0, 1), "0"), # 整数 0(F(5, 1), "5"), # 整数 k(F(1, 2), "1/2"), # 0<fr<1 -> p/q(最简)(F(2, 4), "1/2"), # 自动最简(F(7, 3), "2'1/3"), # fr>1 -> a'b/c(ASCII 单引号)(F(6, 3), "2"), # 可整除 -> 整数],
)
def test_format_value_freeze_rules(fr, expect):assert format_value(fr) == expectdef test_format_value_uses_ascii_quote():"""格式固定用 ASCII 单引号。即便解析接受弯引号,format 仍输出 ' 。"""fr = parse_value("2’1/3") # 注意是弯引号s = format_value(fr)assert s == "2'1/3"@pytest.mark.parametrize("s, expect",[("0", F(0, 1)),("5", F(5, 1)),(" 1/2 ", F(1, 2)), # 前后空白("2'1/3", F(7, 3)), # 直引号("2’1/3", F(7, 3)), # 弯引号],
)
def test_parse_value_ok(s, expect):assert parse_value(s) == expect@pytest.mark.parametrize("s",["1//2", # 语法错误"abc", # 非法"1/0", # 分母为 0"2''1/3", # 引号重复"2'1/0", # 带分数里的分母为 0],
)
def test_parse_value_invalid_raises(s):with pytest.raises(ValueError):parse_value(s)@pytest.mark.parametrize("fr",[F(0, 1),F(5, 1),F(1, 2),F(2, 3),F(10, 4), # 2'1/2F(999, 1000),],
)
def test_format_parse_roundtrip(fr):s = format_value(fr)back = parse_value(s)assert back == fr
test_expr_ast.py
def test_eval_basic_add_sub_mul_div():assert eval_expr(add(n(1), n(2))) == F(3, 1)assert eval_expr(sub(n(5), n(2))) == F(3, 1)assert eval_expr(mul(n(3), n(4))) == F(12, 1)assert eval_expr(div(n(8), n(4))) == F(2, 1)def test_eval_with_fractions():# 1/2 + 1/3 = 5/6e = add(f(1,2), f(1,3))assert eval_expr(e) == F(5, 6)# (2/3) / (4/5) = (2/3) * (5/4) = 10/12 = 5/6e = div(f(2,3), f(4,5))assert eval_expr(e) == F(5, 6)def test_eval_nested_precedence():# (1 + 2) * 3 = 9e = mul(add(n(1), n(2)), n(3))assert eval_expr(e) == F(9, 1)# 1 + 2 * 3 = 7e = add(n(1), mul(n(2), n(3)))assert eval_expr(e) == F(7, 1)def test_eval_divide_by_zero_raises():# 生成阶段会避免,但 eval 遇到非法 AST 应明确抛错with pytest.raises(ZeroDivisionError):eval_expr(div(n(1), n(0)))def test_pretty_precedence_min_paren():# (1 + 2) * 3 -> "(1 + 2) * 3" (低优先级子,需括号)e = mul(add(n(1), n(2)), n(3))assert pretty(e) == "(1 + 2) × 3"# 1 + 2 * 3 -> "1 + 2 * 3"(高优先级子,无需括号)e = add(n(1), mul(n(2), n(3)))assert pretty(e) == "1 + 2 × 3"def test_pretty_subtraction_rules_no_negative_semantics():# 9 - (2 + 3) 必须括号;9 >= 5 合法e = sub(n(9), add(n(2), n(3)))assert pretty(e) == "9 - (2 + 3)"# 7 - 2 * 3 -> "7 - 2 * 3"(乘法优先级高,无需括号;7 >= 6 合法)e = sub(n(7), mul(n(2), n(3)))assert pretty(e) == "7 - 2 × 3"# (5 - 2) - 1 -> "5 - 2 - 1"(左结合可省;5>=2、3>=1 均合法)e = sub(sub(n(5), n(2)), n(1))assert pretty(e) == "5 - 2 - 1"# 5 - (7 - 3) -> 右子为 SUB 必须加括号;5 >= 4 合法e = sub(n(5), sub(n(7), n(3)))assert pretty(e) == "5 - (7 - 3)"def test_pretty_division_rules_noninteger_every_div():# (1 / 2) * 3 -> "1 / 2 * 3"(左子为 DIV 可省;1/2 非整数)e = mul(div(n(1), n(2)), n(3))assert pretty(e) == "1 ÷ 2 × 3"# 1 * (2 / 3) -> "1 * (2 / 3)"(右子为 DIV 必须加)e = mul(n(1), div(n(2), n(3)))assert pretty(e) == "1 × (2 ÷ 3)"# (1 / 2) / 3 -> "1 / 2 / 3"(左结合 DIV 可省;两次 DIV 均非整数)e = div(div(n(1), n(2)), n(3))assert pretty(e) == "1 ÷ 2 ÷ 3"# 1 / (2 / 3) -> "1 / (2 / 3)"(右子 DIV 必须加;两次 DIV 非整数)e = div(n(1), div(n(2), n(3)))assert pretty(e) == "1 ÷ (2 ÷ 3)"def test_pretty_fraction_leaf_format():# 叶子分数统一 p/q,不做带分数e = add(f(1,2), n(1))assert pretty(e) == "1/2 + 1"
其他测试不一一列出
为什么能确定程序正确: pytest 测试集合不仅验证了正常路径,还覆盖了边界、异常、性质(交换/结合/约束)和端到端行为(退出码/I-O 格式),能有效防回归,保证读取-生成/批改-输出这条链条稳。
四、性能分析与改进
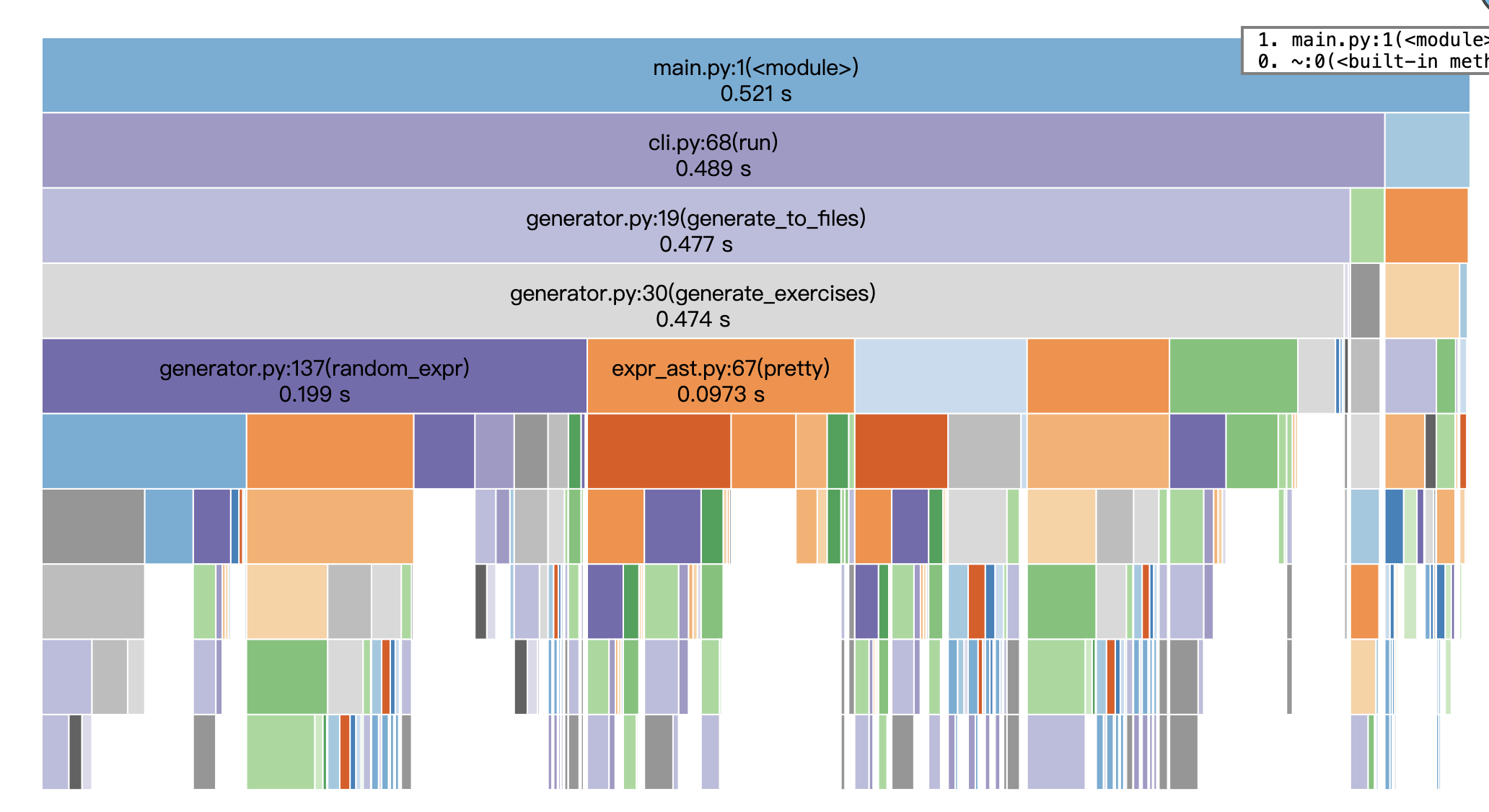
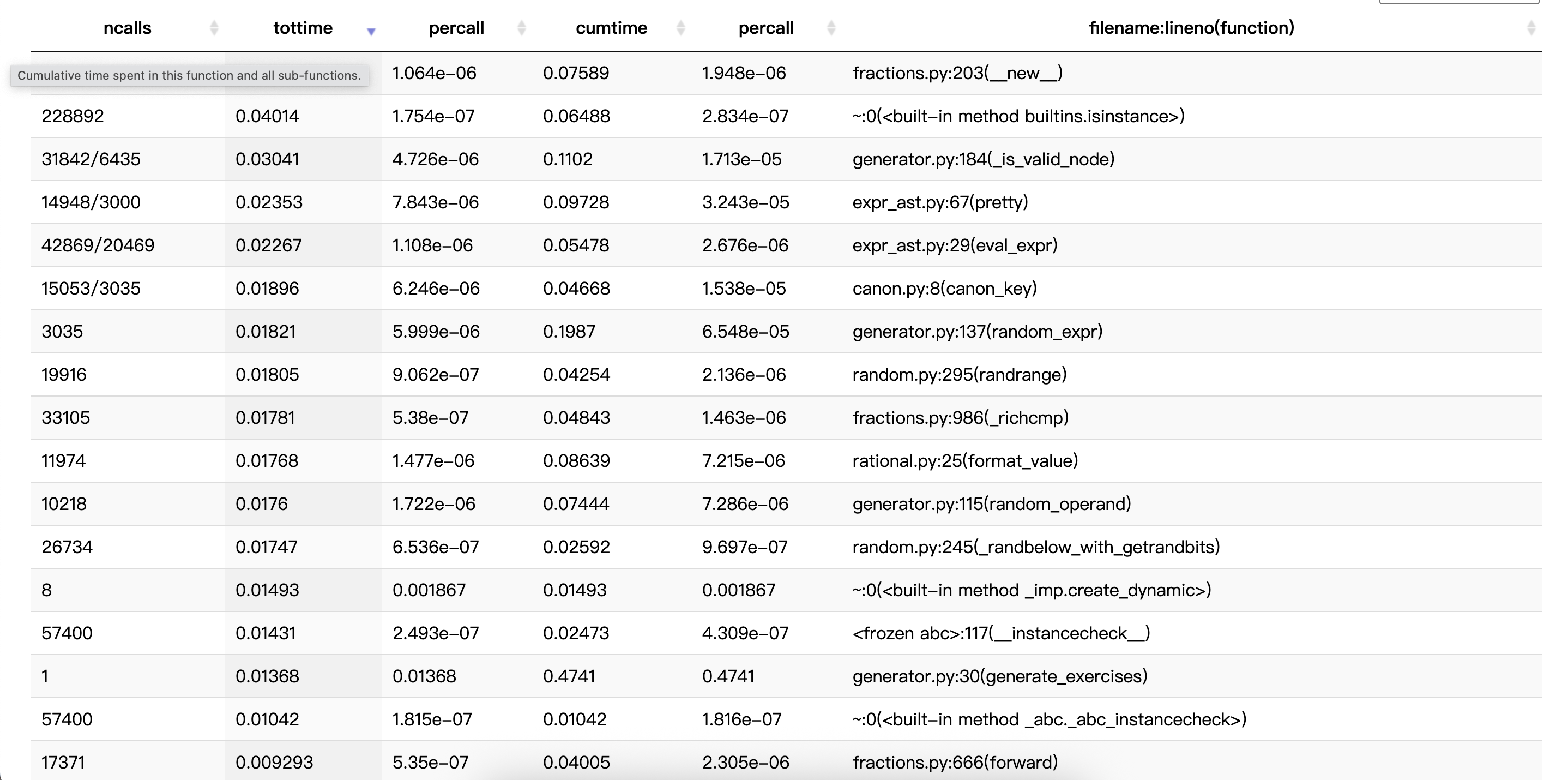
改进思路
- 合并“合法性检查 + 求值”
- 问题:
is_valid_expr在检查 SUB/DIV 时多次递归求值,eval_expr被反复调用。 - 改进:改为一次自底向上的检查函数,同时返回“是否合法 + 子树值”,避免重复遍历与重复求值。
- 延迟渲染 & 复用已算出的值
- 问题:候选表达式在“还未确认保留”时就调用
pretty;答案生成再做一次求值。 - 改进:先合法性检查→去重通过→再渲染题面;答案直接复用上一步得到的数值,不再二次求值。
- 降低
Fraction构造/比较的颗粒开销
- 问题:时间占比中
fractions.__new__、_richcmp、isinstance占比高,说明频繁新建/比较分数。 - 改进:能直接读取分子分母就别重复构造;减少无意义的类型判断;字符串化尽量用已有分子分母。
项目小结
做了什么
搭建了一个可生成四则运算题并批改答案的命令行工具,模块包括:rational、expr_ast、canon、generator、checker、io_utils、cli。
采用 TDD:先写测试再实现,覆盖了整数/分数/带分数解析、最小括号打印、等价去重、随机生成约束、批改容错、I/O 严格格式与 CLI 退出码。
进行了基本效能分析(cProfile),识别生成链路的热点并提出合并检查与求值、延迟渲染、减少重试等改进思路。
合作感想
接口先写,评审再落地,这样沟通成本更低;遇到分歧用测试用例对齐预期;代码评审能及时发现问题点(格式兼容、退出码映射、异常路径)。本地环境/代理/权限问题集中记录与复盘,少走重复弯路。
积累到的经验
要先确定输入输出格式、异常类型与退出码,后续改动更稳。先测后调,抓最大头(重复求值、过早渲染、无效重试),小步验证改动收益。常用命令(pytest、覆盖率、profile)脚本化,避免“没保存/错环境/错 PATH”的无效排障。README、运行命令、目录说明、样例输出,保证他人可复现与接手。
