题意:数轴上有 \(n\) 个人,在 \(x_i\) 处的人以 \(v_i\) 的速度朝正方向匀速运动。初始有某些人携带病毒,当某一时刻两个人相遇时,若其中一个人携带病毒,就会传染给另外一个人。求所有的 \(2^n\) 种初始携带病毒的情况中,使得充分长的时间后,所有人都携带病毒的方案数。对 \(10^9+7\) 取模。
\(n \le 2 \times 10 ^5,1 \le x_i,v_i \le 10^9\),且不存在 \(i\ne j\) 使得 \(x_i=x_j\) 或 \(v_i=v_j\)。
显然充分长的时间后,所有人的相对顺序是按照 \(v_i\) 升序排列。
后文的 \(v,x\) 都是指排序后的结果。
然后这道题的灵魂是,若第 \(i\) 个人初始携带病毒,则他会传染给一段区间内的人。这一段区间 \([l_i,r_i]\) 有,\(l_i\) 是 \(i\) 前面最小的 \(j\),使得 \(x_j > x_i\);\(r_i\) 是 \(i\) 后面最大的 \(j\),使得 \(x_j < x_i\)。
证明的话,感性理解就是画个图。举个例子:
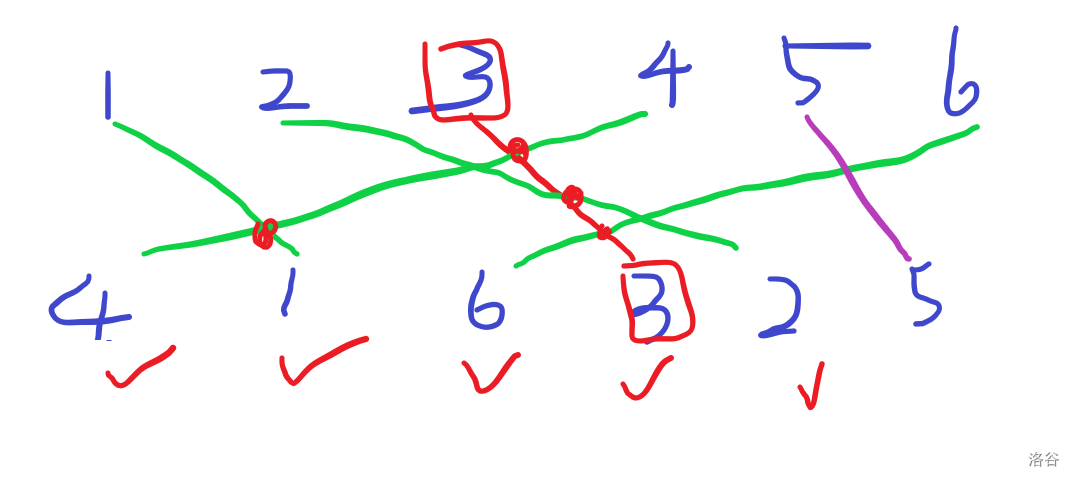
这里 \(x_i=3\) 的 \(l\) 值就是 \(1\)。中间是会存在间接感染的!
然后 \(>l_i\) 的都会被间接感染,\(<l_i\) 的都不会被间接感染。
然后原问题就转化成了,在 \(n\) 个区间 \([l_i,r_i]\) 中选择任意个,使得 \([1, n]\) 都被覆盖。
还有一个性质,就是这 \(l_i,r_i\) 都随 \(x_i\) 的增大而不降!转移的时候就不需要顾虑太多。
接下来随便 DP。树状数组优化转移做到 \(O(n \log n)\)。
#include <bits/stdc++.h>
using namespace std;// #define filename "virus"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define ull unsigned long long
#define all(v) v.begin(), v.end()
#define upw(i, a, b) for(int i = (a); i <= (b); ++i)
#define dnw(i, a, b) for(int i = (a); i >= (b); --i)template<class T> bool vmax(T &a, T b) { return b > a ? a = b, true : false; }
template<class T> bool vmin(T &a, T b) { return b < a ? a = b, true : false; }
template<class T> void clear(T &x) { T().swap(x); }const int N = 2e5+2;const int P = 1000000007;
void vadd(int &a, int b) { a += b; if(a >= P) a -= P; }int n;
pii a[N];struct minBIT {int n;vector<int> c;void init(int n) { this->n = n, clear(c), c.resize(n+5, inf);}void update(int idx, int v) { for(; idx <= n; idx += idx & -idx) vmin(c[idx], v); }int query(int idx) {int res = inf;for(; idx; idx -= idx & -idx) vmin(res, c[idx]);return res;}
};int l[N], r[N];vector<int> range[N];struct BIT {int n;vector<int> c;void init(int n) { this->n = n, clear(c), c.resize(n+5); }void add(int idx, int v) { for(++idx; idx <= n; idx += idx & -idx) vadd(c[idx], v); }int query(int idx) {int res = 0;for(++idx; idx; idx -= idx & -idx) vadd(res, c[idx]);return res;}
} f;void WaterM() {cin >> n;vector<int> vx{-1};upw(i, 1, n) scanf("%d%d", &a[i].first, &a[i].second);sort(a+1, a+n+1, [&] (pii a, pii b) { return a.second < b.second; });upw(i, 1, n) vx.push_back(a[i].first);sort(all(vx)), vx.erase(unique(all(vx)), vx.end());upw(i, 1, n) a[i].first = lower_bound(all(vx), a[i].first) - vx.begin();minBIT tr;tr.init(n);upw(i, 1, n) {tr.update(n - a[i].first + 1, i);l[i] = tr.query(n - a[i].first + 1);}tr.init(n);dnw(i, n, 1) {tr.update(a[i].first, n-i+1);r[i] = n-tr.query(a[i].first)+1;}upw(i, 1, n) range[r[i]].push_back(l[i]);upw(i, 1, n) sort(all(range[i]), greater<int>());//此时l,r都随x[i]的增大单调不降,故没有包含关系,不需要顾虑太多f.init(n+2);f.add(0, 1);int ans = 0;upw(i, 1, n) {int prod = 1, contrib = 0;for(auto l : range[i]) {// int sum = 0;// upw(j, l-1, i-1) vadd(sum, f[j]);vadd(contrib, 1ll * prod * (f.query(i-1) - f.query(l-2) + P) % P);prod = 2ll * prod % P;}f.add(i, contrib), ans = contrib;}cout << ans << '\n';
}signed main() {
#ifdef filenameFileOperations();
#endifsigned _ = 1;
#ifdef multi_casesscanf("%d", &_);
#endifwhile(_--) WaterM();return 0;
}
