「2025 高一上学期笔记 / 日记」
9.1
上午
P10449 费解的开关
25 盏灯排成一个 5×5 的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。若能,输出步数,若不能,输出"-1"
对于这个题目,我们先考虑如何用手简单的推出结果,首先不能乱点灯,我们先考虑从上往下去将 \(0\) 变 \(1\), 对于第一行的话,其实是无所谓其是否点不点,我们对于点 \((x,y)\),我们影响的点只有 \((x,y + 1),(x,y - 1),(x - 1,y),(x + 1,y)\)
所以得出结论就是,想要让第 \(i\) 行第 \(j\) 个点变亮,且不影响 \((i,j)\) 旁边的灯,就只能选择 \((i + 1,j)\) 去点一下,这样就可以了,因为影响的只有第 \(i + 1\) 和 \(i + 2\) 行的,不影响前面的,于是我们可以从上往下递推,直到第 \(n\) 行,此时我们不能再去点任何一个了,因为会影响前面的灯,故,判断一下最后一行是否全是 \(1\) 即可。
到这里还没结束,那第一行到底点不点呢?我们发现由于第一行没有影响,所以是都可以的,我们就可以对于第一行的 \(5\) 个灯进行枚举,这样的就是 \(2 ^ 5 = 32\) 种情况,我们利用位运算枚举组合,\(5\) 位二进制,从 \(00000(0)\) 到 \(11111(31)\) ,进行枚举,按位去操作,如果该位是 \(1\),就点一次。这样就得到了第一行的所有情况,进而推出后面的,保证了正确性。
P2114 [NOI2014] 起床困难综合症
给定 n 个位运算操作(AND、OR、XOR),每个操作有一个参数 t。选择一个初始值 x(0 <= x <= m),让 x 依次经过所有运算后得到的结果最大。求这个最大值。
首先我本来考虑的是对于这个位运算的前后顺序可能没什么太大关系,但是试过样例发现不行,会有问题,于是只能尝试新的思路。
对于我们所选的这个 \(x\) 来说,在二进制下进行的运算是\(\& \| \oplus\),所以不牵扯进位,位与位互相独立,其每一位无论是 \(1\) 还是 \(0\),均有可能对答案有贡献。
因为 \(x \in [0,m]\),且 \(1 \le m \le 1e9\),所以我们的 \(x\) 最大有 \(31\) 位,直接枚举每一位的情况,\(0\) 和 \(1\) 的情况都计算出来,再根据大小去判断取哪个,但是我们为了让答案尽可能的大, 则尽可能的从高位向低位枚举(对于第 \(i\) 位如果不取的话,后面的所有位都取也没第 \(i\) 位取大),取之前判断,如果取后大于 \(m\) 或者不取的贡献更大就不能取。
位运算/状态压缩类题目总结
针对以上两道题目我们发现其区别:
首先是对于两个题目来说,其状态分别是什么?对于第一个题目,状态无非就是第一行每一个灯的操作情况;对于第二个题目,状态就是这个每一位的值的情况。
其实说到最底层,无非是我们对于第一个题目我们想要的是所有的组合方案,因此是去枚举十进制,转二进制后即为所有的情况;第二题我们要的是每一位的取值,因此直接枚举每一位,对于每一位分别取值,由二进制转十进制。
这也是位运算/状态压缩题目的常见的两种处理方式,枚举组合和枚举每位,根据状态的情况,和题目的要求进行判断,选择合适的优化方案。
下午
P10454 奇数码问题
给定整数 n 表示有两个 n * n 的局面,若局面内的数字为 0 则是空格。现在给定两个奇数码游戏的局面,请判断是否存在一种移动空格的方式,使得其中一个局面可以变化到另一个局面。
这个题目的思考深度还是有的,但是呢我们要去考虑的问题是,我们需要找到一个东西,根据这个抽象的东西去直接判断两个局面的可达性。
这个题目其实一开始想到了数字华容道,这个东西很好玩,但是有无解的情况,之前在研究无解的情况的时候,发现,对于这样的情况:
\[\begin{matrix}1 & 2 & 3\\4 & 5 & 6\\8 & 7 & \end{matrix} \]
显然这个东西是无解的,因为 7 与 8 是颠倒的,若想要调换位置,必须调整上面,而上面又是正确的,因此显然无解,而无解的原因在于逆序对的奇偶性。
我们回到题目,把 \(n \times n - 1\) 个数组成一个序列,例如 \([1,2,3,4,6,7,5,8]\),这样的话我们发现其实空格的左右移动并不改变序列,而上下的移动的话,就是把其与前面第 \(n - 1\) 或后面第 \(n - 1\) 个数进行交换,而因为 \(n\) 是奇数,则 \(n - 1\) 必定为偶数,交换后逆序对的奇偶性并不发生改变,所以一个局面无论如何霍霍,其奇偶性都不变,只需要判断两个局面的逆序对奇偶性是否相同就可以。
对于数字华容道,逆序对为偶数才有解,不然怎么拼都拼不好,因为最终目标是 \([1,2,3,4,5,6,7,8]\),这种情况的逆序对为偶数
9.2
上午
P3375 【模板】KMP
给出两个字符串 s1 和 s2,若 s1 的区间 [l,r] 子串与 s2 完全相同,则称 s2 在 s1 中出现了,其出现位置为 l。现在请你求出 s2 在 s1 中所有出现的位置。定义一个字符串 s 的 border 为 s 的一个非 s 本身的子串 t,满足 t 既是 s 的前缀,又是 s 的后缀。对于 s2,你还需要求出对于其每个前缀 s′ 的最长 border t′ 的长度。
对于字符串匹配问题,我们先考虑暴力的做法,利用双指针,\(i,j\),\(i\) 在主串 \(S\) 中,\(j\) 在模式串 \(T\) 中,我们循环让 \(i\) 从 \(1 \to s_{size}\),依次 \(j\) 向后匹配,但是这样的话一旦匹配失败,我们的 \(i\) 向后移动,\(j\) 只能回到 \(1\)。
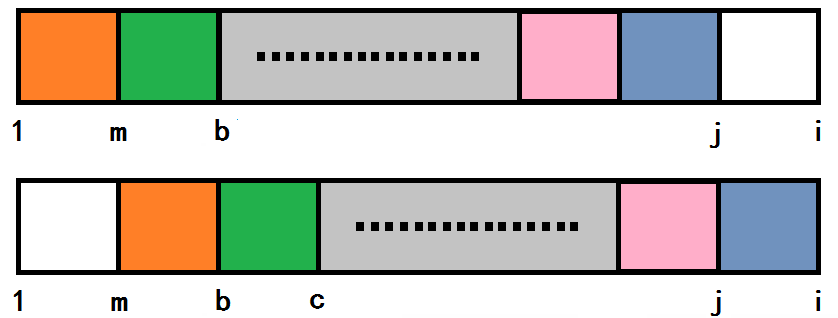
思考一下这样的弊端,我们在 \(i\) 移动时会丢失之前的部分已匹配的信息,我们做以下操作,记录模式串 \(T\) 的 boeder,即 \([1,i]\) 的最长公共前后缀,这样我们可以做出一个滑动操作:
如上图所示,我们可以知道如果我们求出了字符串的 border,在不匹配的时候不必要重新回去判断,直接把字符串向右滑动,继续操作即可。这样就做到了优化操作。
在操作的过程中,我们只需要记录一个 \(nxt\) 数组,\(nxt_i\) 表示模式串 \(T\) 在 \([1,i]\) 的最长公共前后缀长度,如果当前的 \(i\) 与 \(j\) 不匹配,直接 \(j = nxt_j\)(滑动操作),然后继续匹配即可。
计算 nxt 数组:
for(int i = 2, j = 0; i <= b_size; i ++){while(j && B[i] != B[j + 1]) j = nxt[j];if(B[i] == B[j + 1]) j ++;nxt[i] = j;
}
KMP 匹配:
for(int i = 1, j = 0; i <= a_size;i ++){while(j && A[i] != B[j + 1]) j = nxt[j];if(A[i] == B[j + 1]) j ++;if(j == b_size){cout << i - b_size + 1 << '\n';}
}
P4391 [BalticOI 2009] Radio Transmission 无线传输
给你一个字符串 s1,它是由某个字符串 s2 不断自我连接形成的。但是字符串 s2 是不确定的,现在只想知道它的最短长度是多少。
这个题目是循环节问题,与 KMP 相关,我们考虑这样的问题,如果我们对 \(S\) 进行了 nxt 数组的计算,则我们计算出了 \(nxt_n\) 后,可以得到下面的图,对于整个串的最长公共前后缀如下:
我们若是继续向后取段数,对于前缀和后缀,每段取长度 \(m\),则可以得到这样:
而因为前缀等于后缀,且 \(m - 1 = b - m\),因此呢,这个橙色部分就相等了,继续向后取:
所以我们就知道了,无论最后的部分,即 \(i - j\) 的部分是否有余,其实对于我们来说都无所谓,只需要用 \(n - nxt_n\) 就是本题的循环节,就是 \([1,m]\)。
下午
SP263 PERIOD - Period
如果一个字符串 S 是由一个字符串 T 重复 K 次形成的,则称 T 是 S 的循环元。使 K 最大的字符串 T 称为 S 的最小循环元,此时 K 称为最大循环次数。现在给定一个长度为 N 的字符串 S,对 S 的每一个前缀 S[1∼i],如果它的最大循环次数大于 1,则输出该前缀的长度和最大循环次数。
这个题目其实和上道题目差不多,不过这个题目和上道题的区别是,这个题目需要在 \(S\) 的每一个前缀里面的循环节,我们想一想,对于长度为 \(n\) 的 \(S\) 字符串的循环节是 \(n - nxt_n\),则我们是不是可以类比一下,变成 \(i - nxt_i\) 呢?
我们看到这个分段,我们发现,刚才我们说的是对于 \(i - j\) 无论有没有剩余都行,但是在这题里面,我们必须要保证这段也等于 \(m - 1\),其实就是必须要求 \(i \% (i - nxt_i) = 0\),但是这样的话并非正确,如果是 \(nxt_i = 0\) 的话怎么办呢?这样的话 \(i \% (i - nxt_i)\) 必定为 \(0\),我们特判一下即可。
P2536 [AHOI2005] 病毒检测
为了解决这个问题,我们需要判断给定的DNA片段是否与病毒模板片段匹配。病毒模板可能包含通配符:'*'可以匹配0个或任意多个字符,'?'可以匹配任意单个字符。我们的目标是统计出不匹配病毒模板的DNA片段的数量。
对于这个题目,我们如果是对于每一个 RNA 串都去匹配病毒串的话会让时间复杂度出问题,那我们毕竟知道,正难则反,我们为什么不把所有的 RNA 串都存入字典树,再在字典树上跑 dfs,匹配病毒串呢?
好!既然有了想法,那么我们在匹配病毒串的过程中,如果遇到了正常的四个字符 \(\text{ACTG}\) 的话,就无所谓,继续向下一层 dfs。那么 \(*\) 和 \(?\) 怎么办呢?
(1)首先是 \(*\) 的话,就两种情况,第一个是空串,第二个是四个不同的字符。(2)其次是 \(?\) 的话,也是两种情况,第一个是四种字符,第二种是将 \(?\) 替换为 \(*\)。
9.3
上午
P3496 [POI 2010] GIL-Guilds
国王 Byteasar 面临一个严峻的问题。两个相互竞争的贸易组织——裁缝行会(The Tailors Guild)和缝纫行会(The Sewers Guild)同时要求获得许可,在王国每个城镇设立办事处。需要判断是否可以按照规则在城镇中设置办事处,使得每个城镇必须设有本行会的办事处或者该城镇必须直接连接到一个设有本行会办事处的城镇,且不存在某个城镇同时设有两个行会的办事处。
这是一个典型的图论染色问题,需要判断给定的图是否满足特定的染色条件。
首先需要检查图是否连通。如果存在孤立点(没有边连接的顶点),那么该顶点无法满足"自身有办事处或相邻顶点有办事处"的条件,因此直接输出"NIE"。
对于连通图,我们可以将其视为二分图进行染色。将顶点分为两类: 类 \(K\)(裁缝行会办事处),类 \(S\)(缝纫行会办事处)
从任意顶点开始进行深度优先搜索(DFS)或广度优先搜索(BFS),为每个顶点分配颜色:
- 当前顶点染为 \(K\) 色,则其所有邻居染为 \(S\) 色
- 当前顶点染为 \(S\) 色,则其所有邻居染为 \(K\) 色
可行性证明:这种染色方案满足题目要求:
- 每个染色顶点代表设有办事处
- 每个未染色顶点(实际上在这种方案中所有顶点都被染色)至少有一个相邻顶点被染色
- 没有顶点同时被两种颜色染色
P1189 SEARCH
年轻的拉尔夫开玩笑地从一个小镇上偷走了一辆车,车上装有只能发射移动路线方向信息的装置。通过使用小镇的地图,帮助警察局找出汽车最终所有可能的位置。
这是一个基于方向序列的搜索问题,需要模拟汽车按照给定方向移动后的所有可能终点位置。
在每个方向步骤中,汽车可以移动任意多个格子,直到遇到障碍物 \(('X')\) 或地图边界为止。
使用状态 \((x, y, step)\) 表示在第 \(step\) 步时汽车位于位置 \((x,y)\),使用三维数组 \(vis[x][y][step]\) 记录是否已经访问过该状态,避免重复计算
采用深度优先搜索(DFS):
- 对于当前状态 \((x, y, step)\)
- 如果 \(step\) 等于总步数 \(t\),则标记当前位置为可能终点
- 否则,按照第 \(step\) 步的方向一直移动,直到遇到障碍或边界
- 对移动过程中经过的每个位置进行递归搜索
下午
P3956 [NOIP 2017 普及组] 棋盘
有一个 m×m 的棋盘,棋盘上格子可能有红色、黄色或无色。从左上角走到右下角,求花费的最少金币。颜色相同不花费金币,颜色不同花费1金币,可以使用魔法让无色格子暂时变为指定颜色(花费 2金币)。
这是一个带状态记忆的深度优先搜索问题,具有复杂的移动和花费规则。
颜色相同:\(0\) 金币,颜色不同:\(1\) 金币,花费 \(2\) 金币让下一个无色格子变为指定颜色,魔法不能连续使用,只有在离开魔法改变的格子后,才能再次使用魔法
需要记录:
- 当前位置 \((x,y)\)
- 当前总花费
- 是否可以使用魔法
- 前一个格子的颜色(用于判断花费)
遍历所有可能的路径,使用 \(dp[x][y]\) 记录到达 \((x,y)\) 的最小花费,当当前花费已经大于记录的最小花费时,提前返回,考虑四种移动方向(上、下、左、右),遇到无色格子:如果可以使用魔法,则花费 \(2\) 金币并指定颜色,颜色变化:根据前后格子颜色计算花费
搜索类题目类型与解决思路总结
一、基础搜索类型
1. 迷宫路径类(如P1189 SEARCH)
特征:网格地图、障碍物、方向移动
解决思路:
- 使用DFS/BFS遍历所有可能路径
- 注意边界条件和障碍物判断
- 使用记忆化优化重复状态
- 方向处理:将文字方向转换为数字向量
2. 状态空间搜索类(如P3956 棋盘)
特征:复杂状态转移、多种操作、花费计算
解决思路:
- 明确定义状态表示(位置、花费、特殊状态)
- 设计状态转移规则
- 使用DP数组进行记忆化剪枝
- 处理特殊规则(如魔法使用限制)
3. 图论搜索类(如P3496 GIL-Guilds)
特征:图结构、连通性、染色问题
解决思路:
- 构建邻接表/矩阵
- 检查图的连通性
- 使用DFS/BFS进行遍历染色
- 验证染色方案的可行性
解题步骤
第一步:问题分析
- 识别问题类型:判断属于哪种搜索类别
- 确定状态表示:明确需要记录哪些信息
- 分析约束条件:找出所有限制规则
第二步:算法设计
- 选择搜索策略:DFS、BFS或其他变种
- 设计状态转移:定义如何从一个状态到另一个状态
- 制定剪枝策略:如何避免无效搜索
第三步:实现优化
- 数据结构选择:使用合适的数据结构存储状态
- 记忆化设计:设计dp数组或哈希表记录状态
- 边界处理:正确处理各种边界情况
技巧总结
1. 状态压缩技巧
- 使用位运算压缩状态
- 将多维状态映射到一维
- 利用对称性减少状态数
2. 剪枝优化策略
- 可行性剪枝:提前判断是否可能达到目标
- 最优性剪枝:当前解已不如已知最优解时停止
- 记忆化剪枝:避免重复计算相同状态
3. 搜索顺序优化
- 从约束强的分支开始搜索
- 使用启发式信息指导搜索方向
- 合理安排搜索顺序提高效率