《电路基础》第三章学习笔记
任何伟大的事情都不是一蹴而就的,做任何伟大的事情都需要时间、耐心和毅力
I’m back,完成到任务8了,回来继续学习电路!
这一章是本书中最为重要的一章,应给予足够的重视。
主要介绍:1. KCL——节点分析法 2. KVL——网孔分析法
-
节点分析法
-
步骤:
- 选取一个节点作为参考节点(一般是GND),为其余n-1个节点分配电压 \(v_{1}\)、\(v_{2}\)、···、\(v_{n-1}\),这些电压均为相对于参考节点的电位
- 对 n-1 个非参考节点应用KCL列方程组,根据欧姆定律用节点电压来表示各个支路电流
- 求解线性联立方程组从而得到未知的节点电压
-
通过电阻的电流总是由高电位向低电位流动
可表示为
\[i=\frac{v_{higher}-v_{lower}}{R} \] -
求解线性方程组
-
原式:
\[I_{1}=I_{2}+G_{1}v_{1}+G_{2}(v_{1}-v_{2}) \]\[I_{2}+G_{2}(v_{1}-v_{2})=G_{3}v_{3} \] -
矩阵:
\[\begin{bmatrix}G_{1}+G_{2}& -G_{2}\\-G_{2}&G_{2}+G_{3} \end{bmatrix} \begin{bmatrix} v_{1} \\v_{2}\end{bmatrix} =\begin{bmatrix} I_{1}-I_{2} \\I_{2}\end{bmatrix} \]运用矩阵求逆,左式中带G的逆乘到右式的右边,
即可得到 \(v_{1}\) 和 \(v_{2}\) 的表达式。
(其实还可以用克拉默法则等众多方法求解,不过我只会求逆,就不展开其他方法了qwq)
-
-
-
包括电压源的节点分析法
-
如果电压源接在参考节点与非参考节点之间,那么非参考节点的电压就等于电压源的电压。(可以简化电路的分析)
-
如果电压源接在两个非参考节点之间,则这两个非参考节点构成一个广义节点(超节点)。此时可以采用KCL和KVL确定节点电压。
-
超节点:由两个非参考节点和其间的电压源(独立源或受控源)以及与之并联的元件所组成。
- 超节点的属性:
- 超节点内的电压源提供了一个求解节点电压所需的约束方程。
- 超节点本身没有电压
- 包含超节点电路的求解要求同时利用KCL和KVL
- 超节点的属性:
-
-
网孔分析法
- 特点:以网孔电流而不是元件电流作为电流变量,分析起来很方便,而且可以减少联立方程的个数。
- 网孔:内部不包含任何其他回路的一条回路。
- 步骤:
- 为n个网孔分别指定网孔电流 \(i_{1}\),\(i_{2}\),···,\(i_{n}\)
- 对n个网孔分别应用KVL,并根据欧姆定律用网孔电流来表示各个电压。
- 求解n个联立方程,得到网孔电流。
- 应用、计算等和上面基本一样,就不赘述了。
-
包括电流源的网孔分析法
由于电流源的存在,减少了方程的个数,求解反而会更容易一点。
-
电流源仅存在于一个网孔中,设\(i_{2}=-5A\),并对另一个网孔按照通常方法写出网孔方程为:
\[-10+4i_{1}+6(i_{1}-i_{2})=0 \]
-
电流源存在于两个网孔之间,如图,将电流源与之相串联的元件去除后,得到一个超网孔。
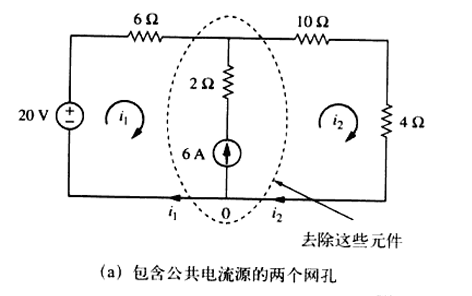
当两个网孔共有一个电流源(独立源或受控源)时,就产生一个超网孔。
-
超网孔的属性:
- 超网孔中的电流源提供了求解网孔电源所需的约束方程
- 超网孔本身没有电流
- 对超网孔要同时应用KVL和KCL
-
-
基于观察法的节点分析与网孔分析(重要)
-
一般而言,如果包含独立电流源的一个电路中具有N个非参考节点,则节点电压方程可以用电导表示为如下形式:
\[\begin{bmatrix} G_{11} & G_{12} & \dots & G_{1N}\\G_{21} & G_{22} & \dots & G_{2N}\\\vdots & \vdots & \vdots & \vdots \\G_{N1} & G_{N2} & \dots &G_{NN} \end{bmatrix} \begin{bmatrix}v_{1}\\v_{2}\\ \vdots \\v_{N} \end{bmatrix} = \begin{bmatrix}i_{1}\\i_{2}\\ \vdots \\i_{N} \end{bmatrix} \]其中:
- \(G_{kk}\)=与节点 k 相连接的各电导之和。
- \(G_{kj}\)=\(G_{jk}\)=直接与节点 k , j 相连接的电导之和的相反数,其中 k≠j。
- \(v_{k}\)=节点 k 处的未知电压
-
-
节点分析法与网孔分析法的比较
- 区分
- 包含大量串联元件、电压源或超网孔的,节点数多于网孔数电路网络更适合采用网孔分析法。
- 包含较多并联元件、电流源或超节点的,节点数少于网孔数的电路网络,则适合节点分析法。
- 妙处
- 可以用一种方法来验证另一种方法得到的结果正确与否
- 区分
