最大熵强化学习(Maximum Entropy RL, SAC)
背景
此前的所有强化学习方法均专注于最大化回报(return),这对应于强化学习中的利用(exploitation):我们只关心最优策略。
而探索(exploration)通常由额外机制实现,例如:
- 基于值函数方法中的 \(\epsilon\)-greedy 或 softmax 策略;
- DDPG 中对动作添加高斯噪声或 OU 噪声。
这些机制通常引入新的超参数(如 \(\epsilon\)、softmax 温度等),且需手动调整其随时间的衰减。
最大熵强化学习(Maximum Entropy RL) 的核心思想是:
让算法自动学习“需要多少探索”才能最有效地学习。
这种思想可追溯至 [@Ziebart2008] 与 [@Todorov2008] 的概率推断视角。
我们先介绍熵正则化(entropy regularization),再讨论 Soft Q-learning 与 Soft Actor-Critic(SAC)。
熵正则化(Entropy Regularization)
熵正则化 [@Williams1991] 在目标函数中加入一个熵项:
其中 \(\beta\) 控制探索强度。
离散策略的熵定义为:
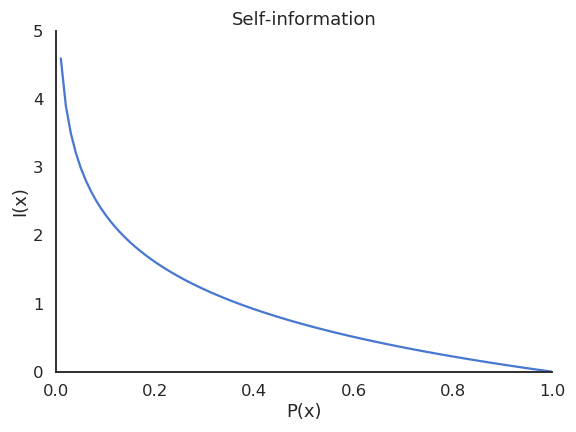
对于连续动作空间,若策略服从高斯分布 \(\pi_\theta(s,a)=\mathcal{N}(\mu_\theta(s),\sigma_\theta^2(s))\),其微分熵为:
熵的意义
- 策略确定性强 → 熵接近 0;
- 策略随机性强 → 熵较大。
通过在目标函数中增加熵项,鼓励策略保持非确定性,即在获取高回报的同时保持足够探索。
若 \(\beta\) 过小 → 熵项作用弱,策略过早收敛为确定性;
若 \(\beta\) 过大 → 策略过度随机,性能下降。
此外,随机策略还能:
- 对抗环境的不确定性(POMDP 中尤为重要);
- 学习多样化的最优解(减少样本复杂度)。
熵正则化如今被广泛用于深度强化学习(如 A3C、PPO、SAC 等)。
Soft Q-learning
传统熵正则化在每个状态中单独最大化策略熵。
@Haarnoja2017 在 最大熵强化学习框架 下推广为Soft Q-learning:
区别在于:Soft Q-learning 最大化的是整条轨迹的熵,即希望智能体访问“高不确定性状态”以减少对环境的无知。
策略可定义为 softmax 形式:
相应的软 Q 值满足:
而软状态值定义为:
该形式在离散动作空间中等价于熵正则化 Bellman 方程。
其关键思想:值函数同时考虑了期望回报与策略的不确定性。
Soft Q-learning 算法
算法流程:
- 从经验回放中采样 \((s,a,r,s')\);
- 计算 \(V_{\text{soft}}(s') = \mathbb{E}_{a'\sim\pi}[Q_{\text{soft}}(s',a') - \log\pi(s',a')]\);
- 更新 Q 函数:\[Q_{\text{soft}}(s,a) \leftarrow r + \gamma V_{\text{soft}}(s') \]
- 更新策略 \(\pi\)(若不直接用 softmax 形式)。
其不足在于:计算 \(V_{\text{soft}}(s')\) 需在连续空间中多次采样,计算复杂。
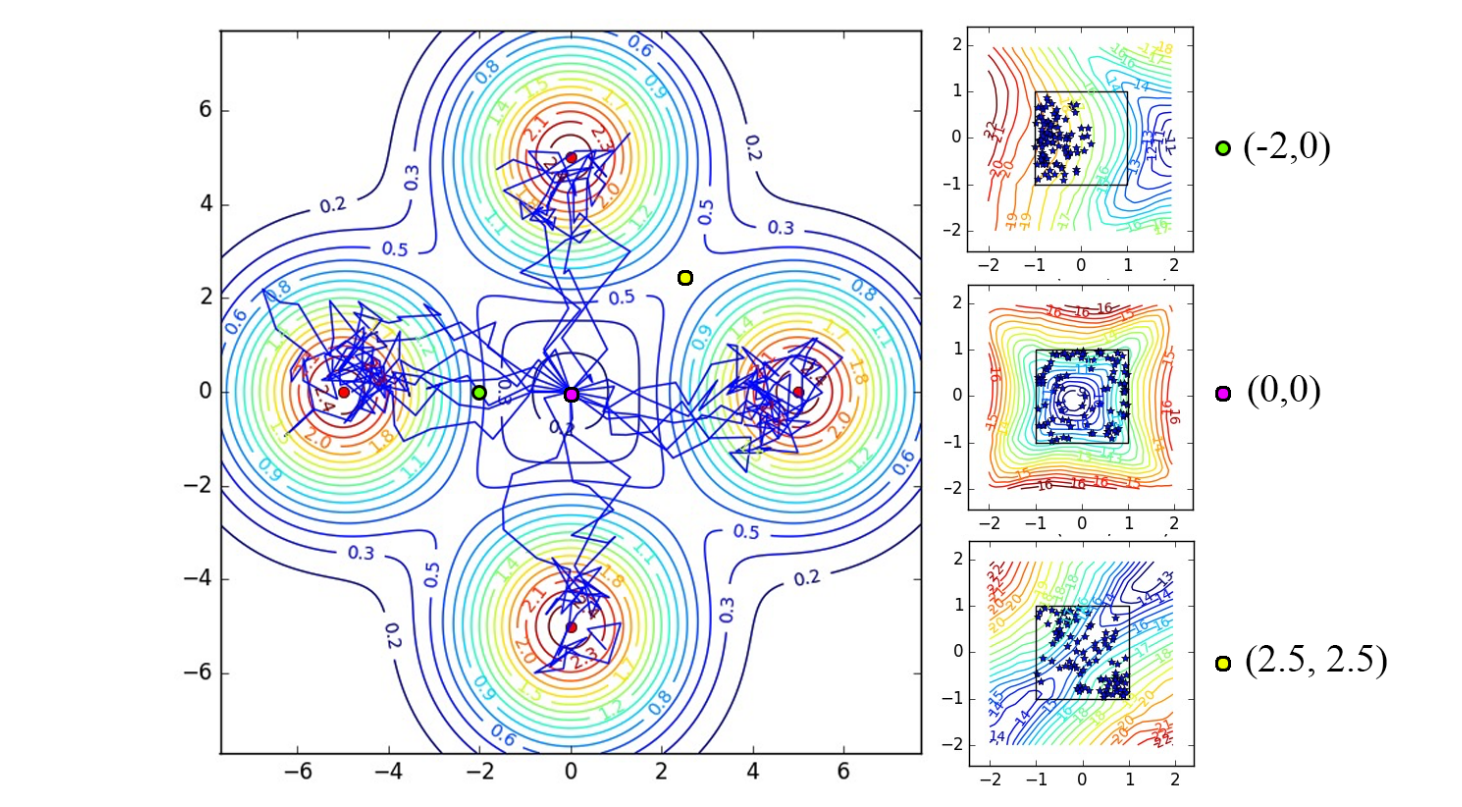
与传统 RL 不同,Soft Q-learning 的策略在收敛后仍保持随机性,可持续探索多种最优策略。
Soft Actor-Critic(SAC)
@Haarnoja2018a 提出的 Soft Actor-Critic (SAC)
是 Soft Q-learning 的可扩展版本,具有以下特征:
- off-policy 学习(使用经验回放);
- 同时学习随机策略与值函数;
- 样本效率与稳定性远超 DDPG、PPO。
网络结构
SAC 包含三个近似器:
| 名称 | 作用 |
|---|---|
| \(V_\varphi(s)\) | 软状态值函数 |
| \(Q_\psi(s,a)\) | 软 Q 值函数 |
| \(\pi_\theta(s,a)\) | 随机策略(Actor) |
损失函数
软状态值网络:
软 Q 网络:
策略网络:
通过最小化 KL 散度,使策略接近 soft Q 分布:
利用重参数化技巧(reparameterization trick)可避免直接计算 \(Z(s)\)。
SAC 算法流程
-
采样 \((s_t,a_t,r_{t+1},s_{t+1})\) 并存入回放池;
-
从回放池中采样批量;
-
采样动作 \(a \sim \pi_\theta(s)\);
-
更新:
- 状态值网络:\[\nabla_\varphi (V_\varphi - (Q_\psi - \log\pi_\theta))^2 \]
- Q 网络:\[\nabla_\psi (r + \gamma V_\varphi' - Q_\psi)^2 \]
- 策略网络:\[\nabla_\theta D_{KL}(\pi_\theta || e^{Q_\psi}/Z) \]
- 状态值网络:
-
定期软更新目标网络。
性能与特点
- off-policy → 高样本复用率;
- 熵调节 → 自动探索与稳定收敛;
- 随机策略 → 适用于高维连续控制任务;
- 双 Q 网络 + 目标网络 → 抑制过估计偏差。
在 MuJoCo 与 Humanoid 等复杂任务上,SAC 的收敛速度与最终性能均超越 DDPG、PPO 等主流算法。
总结
| 算法 | 关键特性 |
|---|---|
| Soft Q-learning | 最大熵目标,基于 Q 更新 |
| DDPG | 确定性策略,off-policy |
| SAC | 最大熵 + off-policy + 随机策略 |
| PPO/TRPO | on-policy,基于信赖域的稳定优化 |
SAC 实现了最大熵强化学习思想的完整落地:
在高维连续动作空间中兼顾高效探索、稳定性与性能。
