(前置:没有在百度百科上找到,查了一下这种方法是由英国经济学家埃拉闫提出的(真·DP起源于经济学))
核心思想:从集合角度分析DP问题
在我们遇到的DP问题中,一般都是求在一个有限集内的最值,但是这些方案数量一般都是指数级别的,想要一个一个查找出来不太可能。所以DP方法是用来优化这种寻找最优方案的过程的。一般的DP分析方法是通过状态,阶段,子问题三个方面来推的,在学习过闫氏分析法之前我一直都是通过先写一遍暴搜再通过转移阶段来推状态转移方程,这种方法很慢,并且有一定理解差异,但是闫氏DP分析法可以从题目本身出发,通过划分集合的方式来代替推方程,使解题过程更加清晰明了。
我们在使用闫氏DP分析法解决DP问题时一般都要经历两个阶段:
- 状态表示(化零为整,寻找共性):一般指把一些具有相似点的方案用一个状态来表示,简单点就是指把问题的答案存在一个状态中来求解。状态表示一般要从两个角度来分析
- [1]集合:确定该状态表示的集合,比如0/1背包问题中,我们把 \(f[i][j]\) (未优化)表示为所有考虑前 \(i\) 个物品且总体积不超过 \(j\) 的最大价值方案的集合。我们通过用 \(f[i][j]\) 来表示一类问题而不是一个东西,这就是DP实现优化的本质
- [2]属性:就是我们状态要存的这个值是这个集合的什么东西,也就是题目要求的最大值/最小值/数量等等
- 状态计算(化整为零,寻找不同):这里就是闫氏DP分析法与替他分析法最大的不同,具体的,我们要把它们划分成若干个不同的子集来求,每一个子集分别去求,比如说0/1背包问题我们将 \(f[i][j]\) 划分成
![]() 可以发现我们将我们找到的状态划分为一个个子集,划分的依据为寻找最后一个不同点。这里还有两个要点:第一就是不要漏情况,这会导致你的状态转移方程错误从而寄掉;第二如果是在求值或是求数量的时候,要保证没有重复,否则就会导致结果出错。通过以上过程,我们实际上是把一个大的问题直接分为了几个小问题解决,这就是所说的化整为零。
可以发现我们将我们找到的状态划分为一个个子集,划分的依据为寻找最后一个不同点。这里还有两个要点:第一就是不要漏情况,这会导致你的状态转移方程错误从而寄掉;第二如果是在求值或是求数量的时候,要保证没有重复,否则就会导致结果出错。通过以上过程,我们实际上是把一个大的问题直接分为了几个小问题解决,这就是所说的化整为零。
例题:
一、背包DP
1. 0/1背包问题
题目链接
按照我们上面的闫氏DP分析法,我们得到以下过程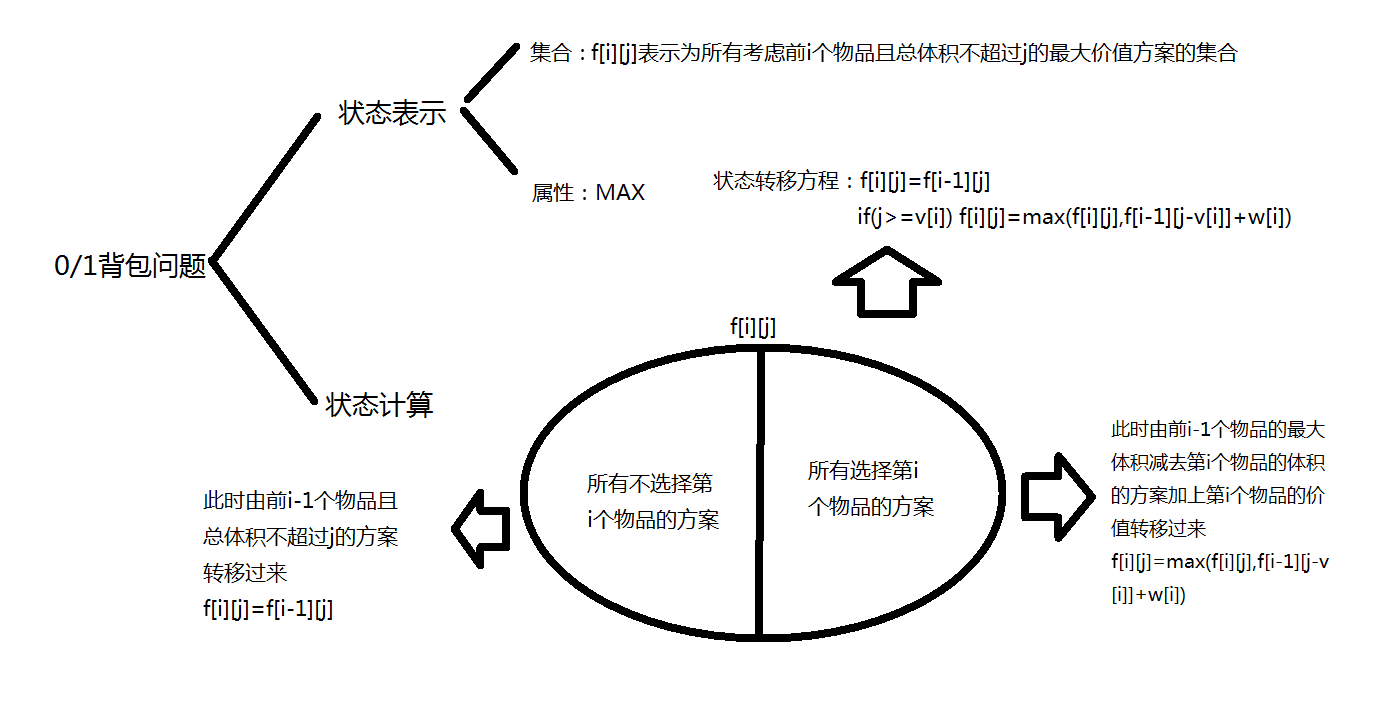 这样,我们可以轻松得到未优化过的状态转移方程,代码如下
这样,我们可以轻松得到未优化过的状态转移方程,代码如下
#include<bits/stdc++.h>
using namespace std;
const int N=1018;
int n,m,w[N],v[N],f[N][N];
int main(){scanf("%d%d",&m,&n);for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&w[i]);for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}printf("%d",f[n][m]);return 0;
}
注意到空间复杂度 \(O(NM)\) 会被黑心出题人给卡 \(MLE\) ,我们就不能用两维数组来解决这个问题,我们可以使用滚动数组解决,这里不过多讲解,有兴趣可以看看代码,这里我们在上面程序的基础上进行缩维优化。容易发现,在每个阶段转移时,我们实际上只是进行了一次从 \(f[i][]\) 到 \(f[i-1][]\) 的拷贝操作,即我们可以将 \(f[i][j]\) 的第一维省略掉,即现在的状态表示为 \(f[j]\) 表示所有考虑到前 \(i\) 个物品,且背包内总体积不超过 \(j\) 的最大价值,同时我们省去上面程序中 \(if(j>=v[i])\) 的特判,将 \(j\) 从 \(m\) 一直枚举到 \(v[i]\) ,这样就可以避免了当前总体积加上 \(v[i]\) 超过 \(j\) 的情况,于是我们就得到了新的状态转移方程: \(f[j]=max(f[j],f[j-v[i]]+w[i])\) 。优化代码如下
#include<bits/stdc++.h>
using namespace std;
const int N=1018;
int n,m,w[N],v[N],f[N],ans=-1;
int main(){scanf("%d%d",&m,&n);for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&w[i]);for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);for(int i=0;i<=m;i++)ans=max(ans,f[i]);printf("%d",ans);return 0;
}2.完全背包
题目链接
这道题虽然只是上面那个题多加了一个可以取多次的条件,即状态表示过程于0/1背包相同,但用闫氏DP分析法可以发现状态计算过程与上面那个题完全不一样,0/1背包问题划分的依据是选或不选第 \(i\) 个物品,而完全背包问题划分的依据是选择几个第 \(i\) 个物品,分析过程为: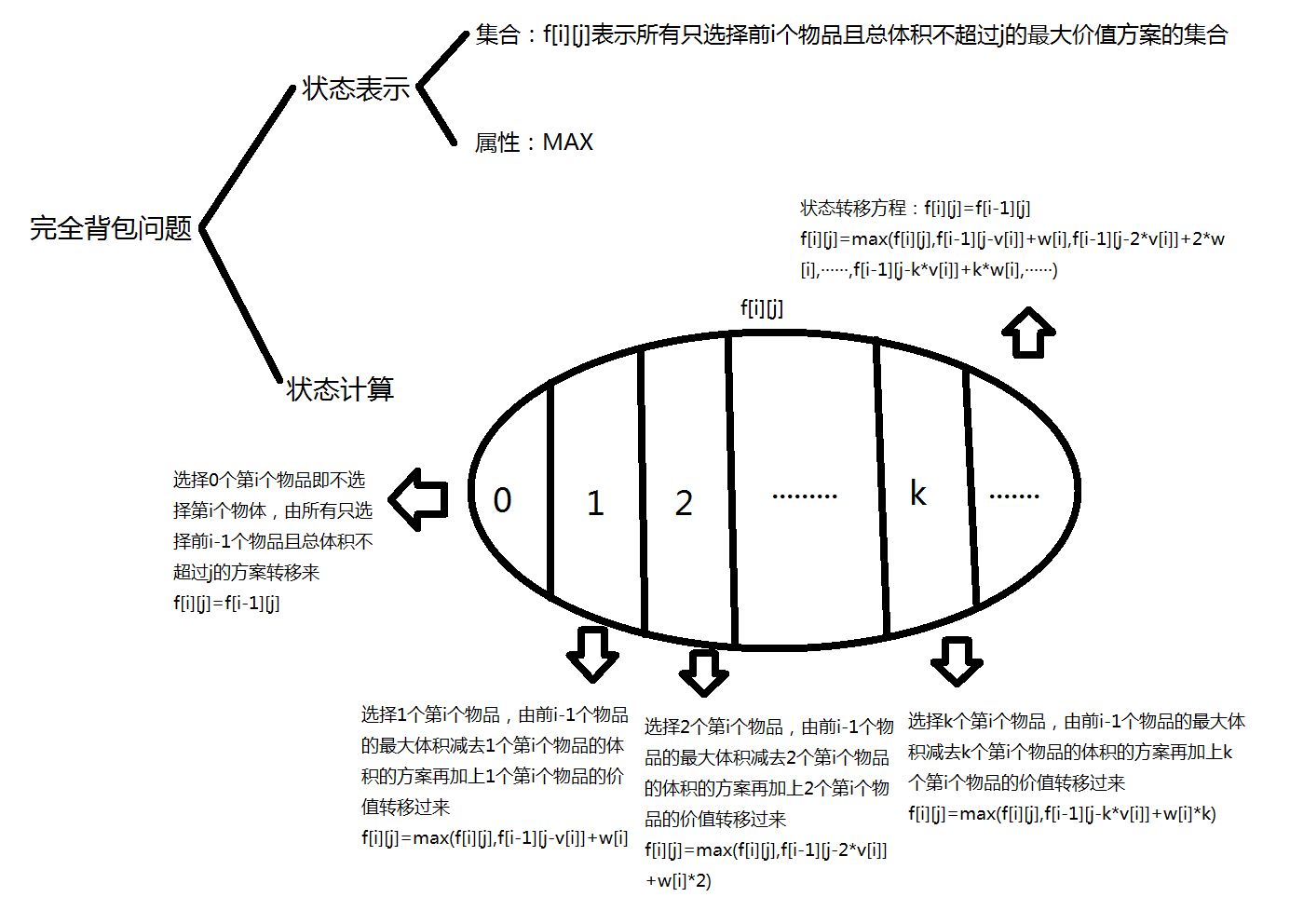 我们发现这么推出来的状态转移方程需要三重循环,在 \(n=10^3\) 的级别下会 \(TLE\) ,我们要对其进行优化。
我们发现这么推出来的状态转移方程需要三重循环,在 \(n=10^3\) 的级别下会 \(TLE\) ,我们要对其进行优化。
注意到:
\(f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i],f[i-1][j-2*v[i]]+2*w[i],······,f[i-1][j-k*v[i]]+k*w[i],······)\)
对于
\(f[i][j-v[i]]=max(f[i-1][j-v[i]],f[i-1][j-2*v[i]]+w[i],f[i-1][j-3*v[i]]+2*w[i],······,f[i-1][j-(k+1)*v[i]]+k*w[i],······)\)
可以发现第一个式子中 \(max(f[i-1][j-v[i]]+w[i],f[i-1][j-2*v[i]]+2*w[i],······,f[i-1][j-k*v[i]]+k*w[i],······)\) 就是第二个式子加上 \(w[i]\) 即第一个式子可以优化为:
\(f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i])\)
这样我们就得到了优化过后的状态转移方程,进而得到代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1018;
int f[N][N],n,m,w[N],c[N];
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)scanf("%d%d",&w[i],&c[i]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){f[i][j]=f[i-1][j];if(j>=w[i])f[i][j]=max(f[i][j],f[i][j-w[i]]+c[i]); }printf("%d",f[n][m]);return 0;
}
但是这个题目有点阴间,直接把上面代码交上去会 \(RE\) 拿 \(50\) 分,因为这个题的 \(m\) 的范围开到了 \(10^5\) 级别,导致数组会爆炸(其实有点手法也能过),我们可以用滚动数组来做,也可以像0/1背包问题一样进行缩维,具体过程与0/1背包类似,在这不过多说明(雾),代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int m,n,w[N],v[N],f[N];
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)scanf("%d%d",&w[i],&v[i]);for(int i=1;i<=n;i++)for(int j=w[i];j<=m;j++)f[j]=max(f[j],f[j-w[i]]+v[i]);printf("%d",f[m]);return 0;
}
3.分组背包问题
题目链接
二、区间DP
1.石子合并
题目链接
这道题目大家也许并不陌生,通过题目描述我们发现石子最终会被合并成一堆,即该题为一个有限集,而且可以注意到一共有 \((n-1)!\) 种情况,而 \(n\) 的范围又是 \(n<=300\) ,所以直接枚举每种情况是不现实的,我们通过闫氏DP分析法来考虑DP做法: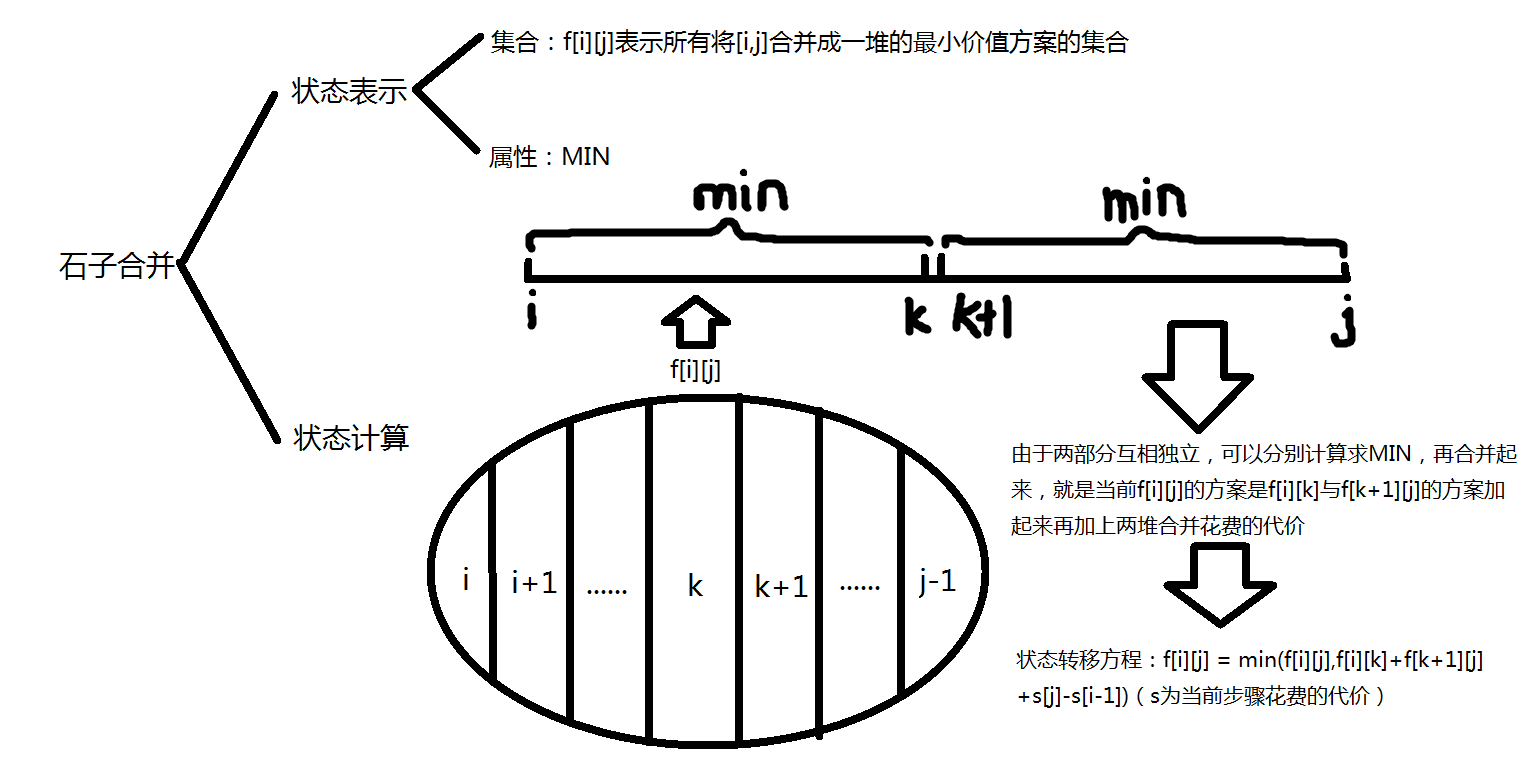 我们知道最后的答案一定是由两堆石子合并起来的,这就是这道题最后一个不同点,通过这个可以划分为不同子集,即最后两堆石子是从哪里开始分开的,对于每个 \(f[i][j]\) 可以从 \(i\) 一枚举到 \(j-1\) (因为要保证两段都有石子)为最后两堆石子的分界线,上图中是以 \(k (i<=k<=j-1)\) 为分界线做的例子,可以得到状态转移方程:
我们知道最后的答案一定是由两堆石子合并起来的,这就是这道题最后一个不同点,通过这个可以划分为不同子集,即最后两堆石子是从哪里开始分开的,对于每个 \(f[i][j]\) 可以从 \(i\) 一枚举到 \(j-1\) (因为要保证两段都有石子)为最后两堆石子的分界线,上图中是以 \(k (i<=k<=j-1)\) 为分界线做的例子,可以得到状态转移方程:
\(f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1])\)
\(s[]\) 数组可以通过前缀和来解决,代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1018;
int n,s[N],f[N][N];
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&s[i]);s[i]+=s[i-1];//处理前缀和}for(int len=2;len<=n;len++){//枚举区间长度 for(int i=1;i+len-1<=n;i++){//枚举区间右端点 int j=i+len-1;//得到区间左端点 f[i][j]=1<<30;for(int k=i;k<j;k++)//枚举最后两堆得分界线 f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);}}printf("%d",f[1][n]);return 0;
}
2.回文字串
题目链接
三、线性DP
1.最长公共子序列问题(LCS)
题目链接
这道题相信大家已经很熟悉了吧,我们可以发现最坏情况下一一枚举是 \(2^n\) 的级别,是不现实的,我们还是用闫氏DP分析法来做DP做法,过程如下: 累了,也许烂尾了吧,以后在写
累了,也许烂尾了吧,以后在写

 可以发现我们将我们找到的状态划分为一个个子集,划分的依据为寻找最后一个不同点。这里还有两个要点:第一就是不要漏情况,这会导致你的状态转移方程错误从而寄掉;第二如果是在求值或是求数量的时候,要保证没有重复,否则就会导致结果出错。通过以上过程,我们实际上是把一个大的问题直接分为了几个小问题解决,这就是所说的化整为零。
可以发现我们将我们找到的状态划分为一个个子集,划分的依据为寻找最后一个不同点。这里还有两个要点:第一就是不要漏情况,这会导致你的状态转移方程错误从而寄掉;第二如果是在求值或是求数量的时候,要保证没有重复,否则就会导致结果出错。通过以上过程,我们实际上是把一个大的问题直接分为了几个小问题解决,这就是所说的化整为零。