题目传送门
绝世好题
让我学会了分层图的真正用法
以前都只会自作聪明地分两层:
美其名曰【正图】【反图】
现在知道了还有这种神奇的建图方法!
理解题意:
有向图
给定起点终点
求路径上两点买卖东西最大收益
思路:
考虑建分层图
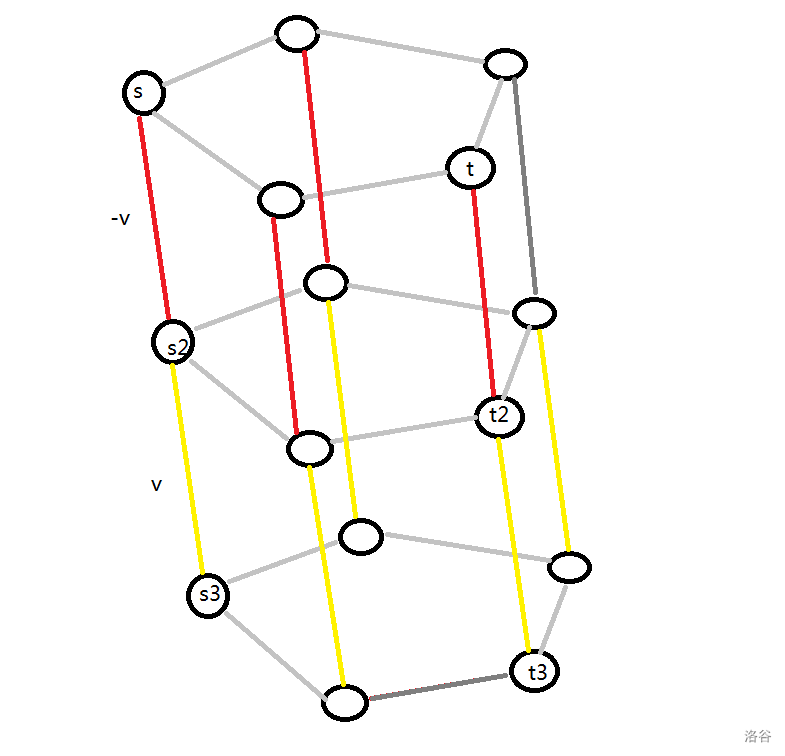
所以此时问题从二维图s->t
转化为了
三维图(分层图)中的s->t3
我们对于层之间的边怎么操作呢?
其实每层对应着不同的状态
- 第一层对应没有买入
- 第二层对应已经买入
- 第三层对应已经卖出
从第一层到第二层的边就是 -v ,负的价格,表示此时买入
从第二层到第三层的边就是 v ,正的价格,表示此事卖出
而我们让同一层之间的边的权值为 0 , 仅仅只检测连通性就好了
建图建完(最繁重的工作)那么我们只需要跑一边SPFA求出第一层的起点到第三层的终点
(经历了一次买入和一次卖出的路径)
就解决了这个问题
\(\mathbb {CODE}\)
#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;int n, m;
int dis[N * 3], vis[N * 3];
vector<pair<int, int> > e[N * 3];void add(int u, int v)
{e[u].push_back({v, 0});e[u + n].push_back({v + n, 0});e[u + n + n].push_back({v + n + n, 0});
}void solve()
{memset(dis, -0x3f, sizeof dis);queue<int> q;q.push(1);vis[1] = 1;dis[1] = 0;while (!q.empty()) {int u = q.front();q.pop();vis[u] = 0;for (auto t : e[u]) {int v = t.first, w = t.second;if (dis[v] < dis[u] + w) {dis[v] = dis[u] + w;if (!vis[v]) {q.push(v);vis[v] = 1;}}}}
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;for (int i = 1; i <= n; i++) {int price;cin >> price;e[i].push_back({i + n, -price});e[i + n].push_back({i + n + n, price});}for (int i = 1; i <= m; i++) {int u, v, id;cin >> u >> v >> id;add(u, v);if (id ^ 1)add(v, u);}solve();cout << dis[n * 3] << endl;return 0;
}