CD78.【C++ Dev】以AVL任务的bug讲讲调试技巧
目录
1.有bug的项目源代码
AVLTree.h
main.cpp
2.查错过程
树的结构有没有问题?
技巧1:使用调用堆栈回溯
技巧2:监视窗口查看变量
技巧3:写辅助函数
设计函数的框架
具体细节处理
顺便解决OJ题
回到查错的任务
技巧4:下断点
方法1:条件断点
方法2:内联汇编(int 3)
方法3:MSVC的__debugbreak()
3.验证AVL树的方法
1.有bug的项目源代码
AVLTree.h
只实现了插入函数
#pragma once
#include
#include
using namespace std;
template
struct AVLTreeNode
{
pair _kv;
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;
int _bf; // balance factor
AVLTreeNode(const pair& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{
}
};
template
class AVLTree
{
typedef AVLTreeNode Node;
public:
bool insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first _right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first _right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else // if (cur == parent->_right)
{
parent->_bf++;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
break;
}
else
{
assert(false);
}
}
return true;
}
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
Node* grandparent = parent->_parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (grandparent->_left == parent)
{
grandparent->_left = cur;
}
else
{
grandparent->_right = cur;
}
cur->_parent = grandparent;
}
parent->_bf = cur->_bf = 0;
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
curright->_parent = parent;
Node* grandparent = parent->_parent;
cur->_right = parent;
//parent->_parent = cur;
if (grandparent == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (grandparent->_left == parent)
{
grandparent->_left = cur;
}
else
{
grandparent->_right = cur;
}
cur->_parent = grandparent;
}
parent->_bf = cur->_bf = 0;
}
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
int bf = curleft->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
cur->_bf = 0;
curleft->_bf = 0;
parent->_bf = 0;
}
else if (bf == 1)
{
cur->_bf = 0;
curleft->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
cur->_bf = 1;
curleft->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
int bf = curright->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curright->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
cur->_bf = 0;
curright->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
cur->_bf = -1;
curright->_bf = 0;
}
}
private:
Node* _root = nullptr;
};main.cpp
#include "AVLTree.h"
using namespace std;
int main()
{
AVLTree tree;//测试单关键字
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
for (auto e : a)
tree.insert(make_pair(e,nullptr));
return 0;
}运行结果:
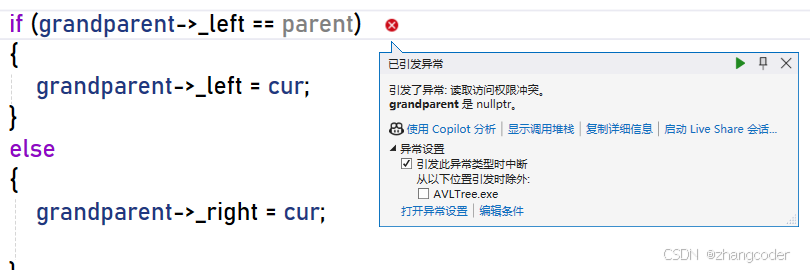
在RotateLight函数中引发空指针访问,出错
2.查错过程
树的结构有没有问题?
上面显示grandparent是nullptr,推断:如果树的结构没问题,那么parent一定是根节点
parent真的是根结点吗?
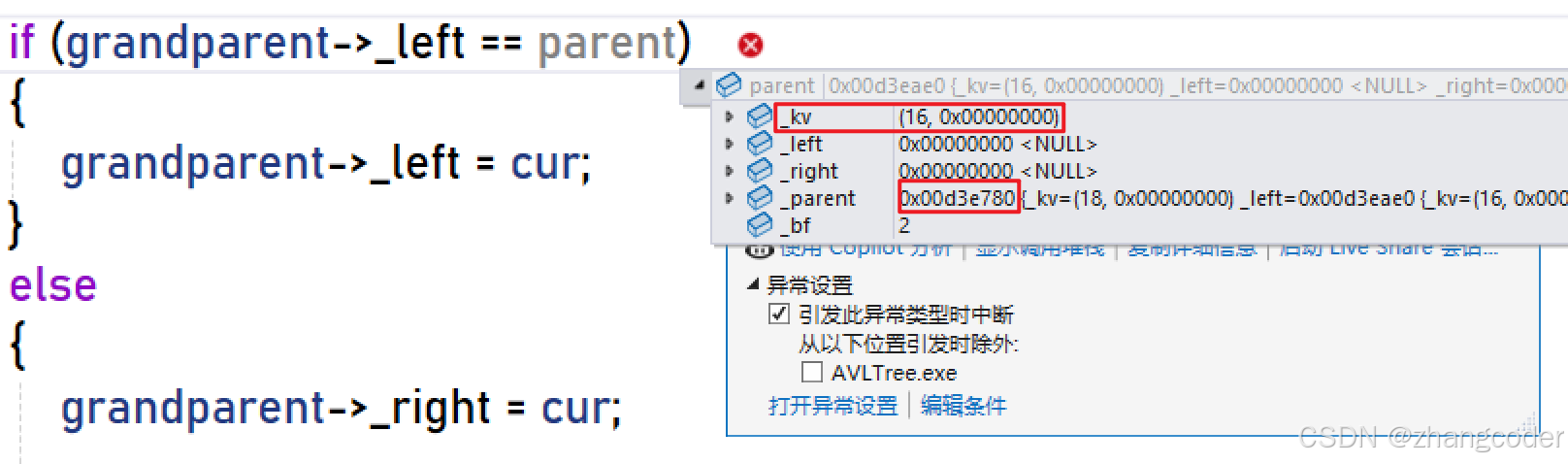
出错代码处显示parent的_parent不为空,这是不正常的,无法退出parent是根节点这个论断,所以得出结论:树的结构有问题-->得出某次旋转出问题了
技巧1:使用调用堆栈回溯
单击异常窗口中的"显示调用堆栈",或者单击菜单栏中的选项
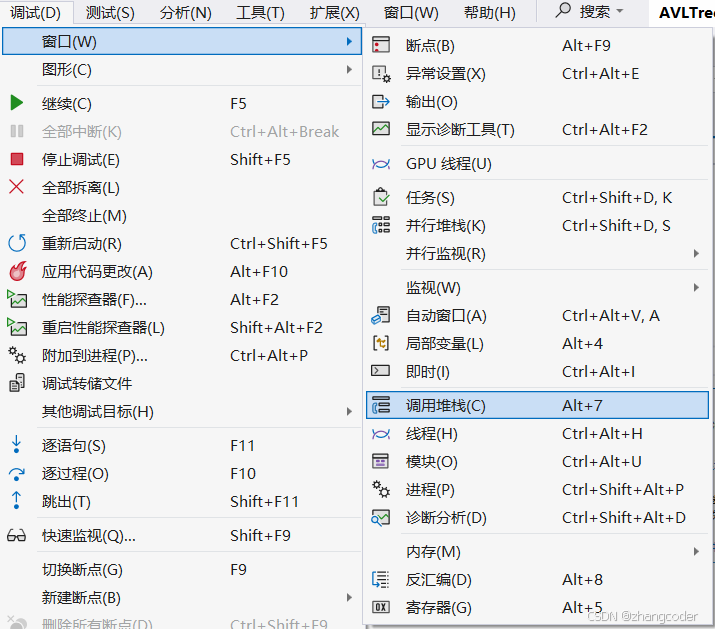
双击可以回溯: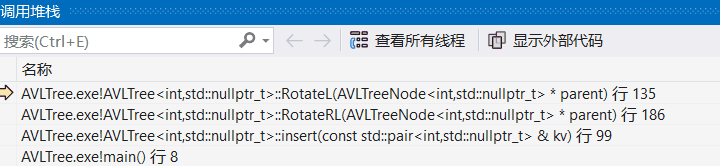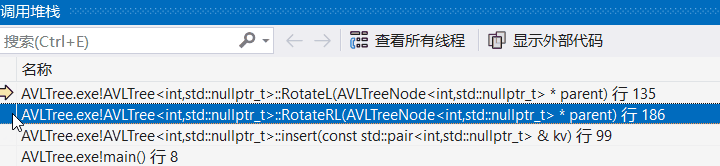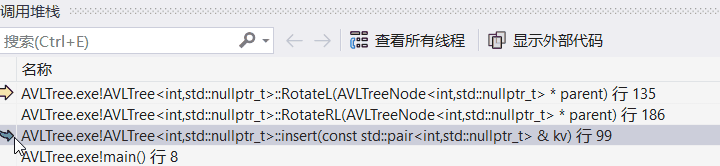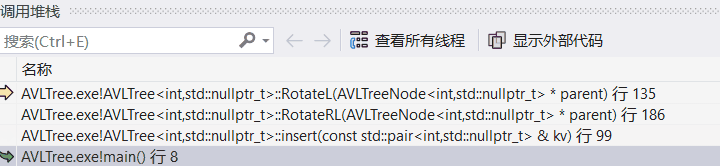
回溯到insert函数,发现是插入18出问题了
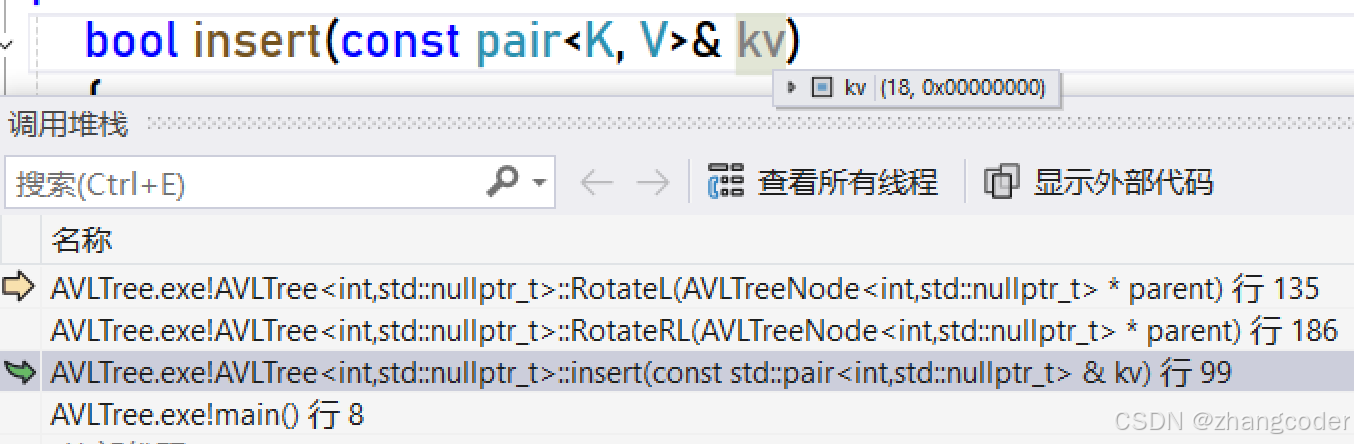
main.cpp中的插入顺序为:
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };技巧2:监视窗口查看变量
从parent来看,监视窗口显示已经插入的节点为(16,nullptr)、(18,nullptr)、(26,nullptr)
1.发现(3,nullptr)、(7,nullptr)、(11,nullptr)和(9,nullptr)节点被丢掉了

2.节点重复出现
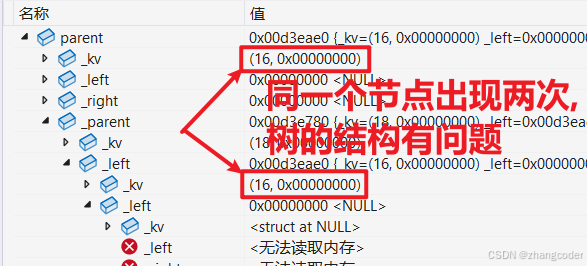
可以得出:插入(18,nullptr)节点之前就旋转出错了
常规方法是一个一个插入节点然后画树的结构图分析有没有问题,但这样做太消耗时间
技巧3:写辅助函数
可以写一个is_balance函数来辅助调试
is_balance函数的目的是判断树是否平衡(注:验证平衡性,不一定满足二叉搜索树)
实现算法: 分别算所有左右子树的高度,然后作差,确保绝对值<=1,可以使用递归
重要提醒: 一定不能看平衡因子,容易"监守自盗",即可能平衡因子的更新是错的
设计函数的框架
bool is_balance()//共有
{
return _is_balance(root);
}
//外部调用是没有Node*参数可传的
bool _is_balance(Node* root)//私有
{
//先写递归返回条件: 如果递推完了,就层层返回
//计算左树高度left_height,需要调用递归函数
//计算右数高度right_height,需要调用递归函数
//如果平衡因子异常,提示开发者
//返回abs(left_height-right_height)<=1的真假
}具体细节处理
递归返回条件:root==nullptr:
if (root == nullptr)
return true;计算左右高度:
int left_height = calc_height(root->_left);
int right_height = calc_height(root->_right);实现高度计算函数calc_height:
分而治之的方法: 子树的高度==根的高度(即1)+左右子树中最高的那棵树
int calc_height(Node* root)
{
if (root == nullptr)
return 0;
return max(calc_height(root->_left), calc_height(root->_right)) + 1;
}如果平衡因子异常,打印提示信息:
if (right_height-left_height != root->_bf)
{
cout _bf;
}返回条件:如果有一棵子树不平衡那么整棵树就不平衡,显然需要用与运算,符合"一假全假"的特点
return abs(left_height - right_height) _left) \
&& _is_balance(root->_right);_is_balance函数完整的代码:
bool _is_balance(Node* root)
{
//先写递归返回条件: 如果递推完了,就层层返回
if (root == nullptr)
return true;
//计算左树高度left_height,需要调用递归函数
int left_height = calc_height(root->_left);
//计算右数高度right_height,需要调用递归函数
int right_height = calc_height(root->_right);
if (right_height-left_height != root->_bf)
{
cout _bf;
return false;
}
//返回abs(left_height-right_height)_left) \
&& _is_balance(root->_right);
}main函数中打印提示信息:
#include "AVLTree.h"
using namespace std;
int main()
{
AVLTree tree;//测试单关键字
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
for (auto e : a)
{
tree.insert(make_pair(e, nullptr));
cout << "插入" << e << ",";
if (tree.is_balance())
cout << "树是平衡的" << endl;
else
cout << "树是**不**平衡的" << endl;
}
return 0;
}顺便解决OJ题
Leetcode:
https://leetcode.cn/problems/balanced-binary-tree/description/
给定一个二叉树,判断它是否是平衡二叉树
示例 1:
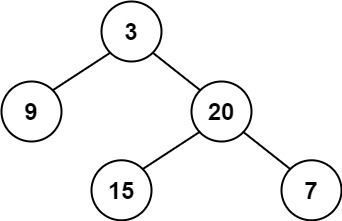
输入:root = [3,9,20,null,null,15,7] 输出:true示例 2:
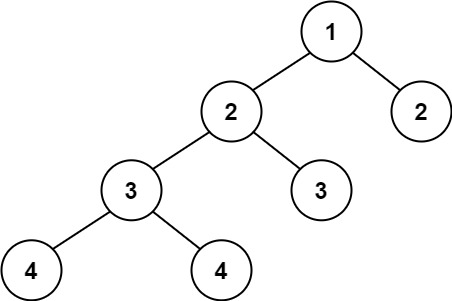
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false示例 3:
输入:root = [] 输出:true提示:
- 树中的节点数在范围
[0, 5000]内-104 <= Node.val <= 104
代码:
稍微修改上方代码即可:
class Solution {
public:
int calc_height(TreeNode* root)
{
if (root==nullptr)
return 0;
return max(calc_height(root->left), calc_height(root->right)) + 1;
}
bool isBalanced(TreeNode* root)
{
if (root == nullptr)
return true;
int left_height = calc_height(root->left);
int right_height = calc_height(root->right);
return abs(left_height - right_height) left) \
&& isBalanced(root->right);
}
};提交结果:
牛客网:
https://www.nowcoder.com/practice/8b3b95850edb4115918ecebdf1b4d222
描述
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
样例解释:
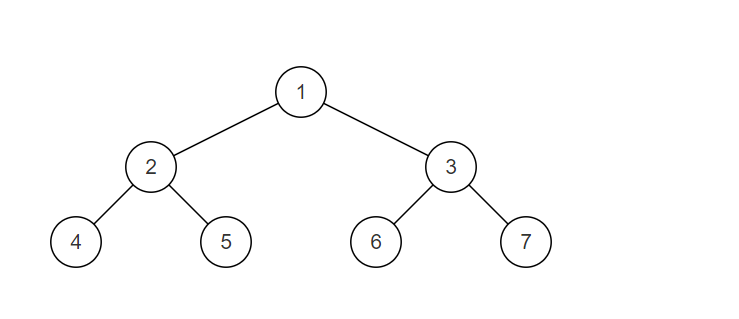
样例二叉树如图,为一颗平衡二叉树
注:我们约定空树是平衡二叉树。
数据范围:n≤100n≤100,树上节点的val值满足 0≤n≤10000≤n≤1000
要求:空间复杂度O(1)O(1),时间复杂度 O(n)O(n)
输入描述:
输入一棵二叉树的根节点
返回值描述:
输出一个布尔类型的值
示例1
输入:
返回值:{1,2,3,4,5,6,7}true示例2
输入:
返回值:{}true
和leetcode题目一样,
class Solution {
public:
int calc_height(TreeNode* root)
{
if (root==nullptr)
return 0;
return max(calc_height(root->left), calc_height(root->right)) + 1;
}
bool IsBalanced_Solution(TreeNode* root)
{
if (root == nullptr)
return true;
int left_height = calc_height(root->left);
int right_height = calc_height(root->right);
return abs(left_height - right_height) left) \
&& IsBalanced_Solution(root->right);
}
};提交结果:
回到查错的任务
写辅助函数能快速定位到出问题的地方,运行结果:插入11时树不平衡
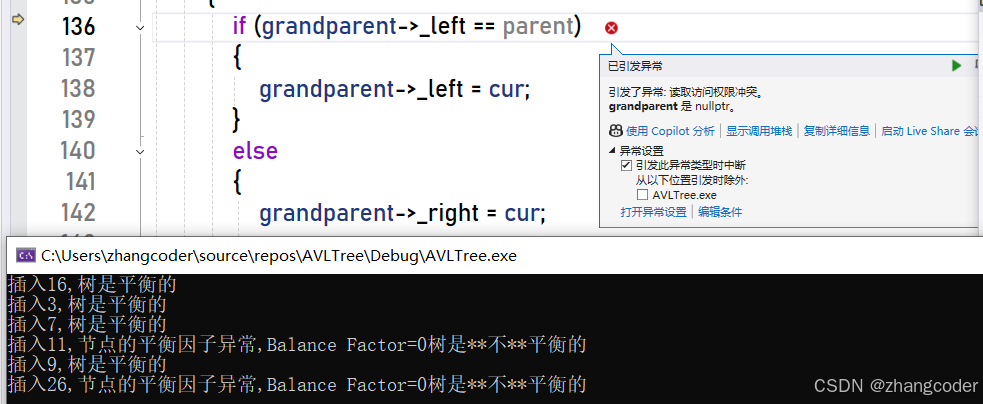
技巧4:下断点
为方便定位到插入11时执行的函数,有两种比较快的方法
方法1:条件断点
右击插入条件断点

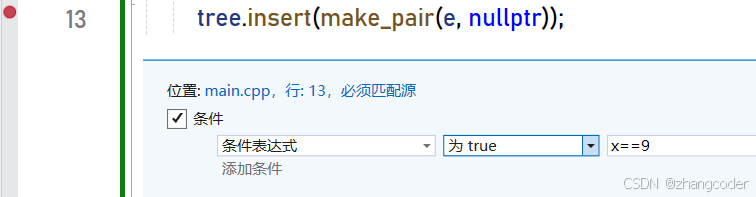
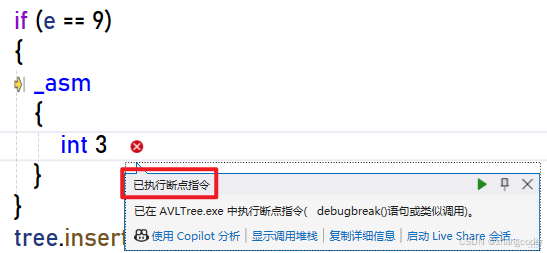
方法2:内联汇编(int 3)
针对于Windows的VS下的x86平台(注: MSVC 编译器在x64目标平台上根本不支持内联汇编),可以这样使用汇编指令下条件断点:
这样就能在指定条件满足时,让进程执行int 3指令停下来
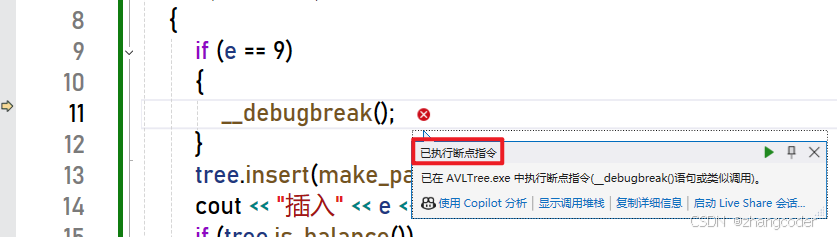
方法3:MSVC的__debugbreak()
无论是Windows的VS下的x86还是x64平台,__debugbreak()都适用,执行该函数就能让进程停止执行代码
当16, 3, 7, 11插入完时,查看监视窗口:
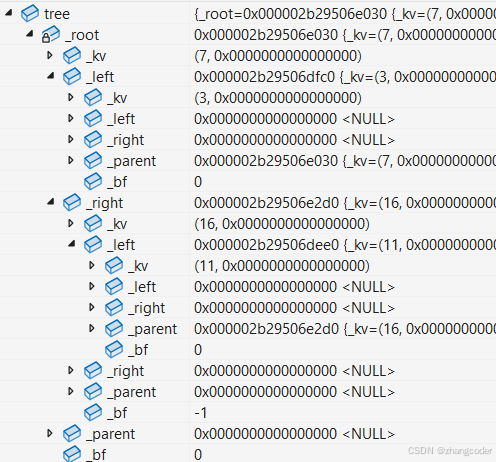
画图为:
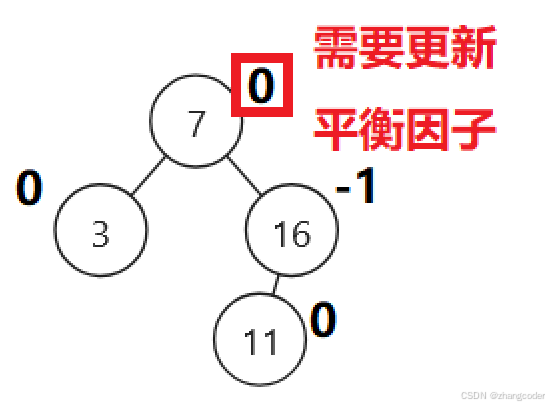
发现问题:平衡因子没有及时更新
改成如下代码:
if (e == 11)
{
__debugbreak();
}接着查查旋转函数的问题,进入insert函数:
先调用RotateR:

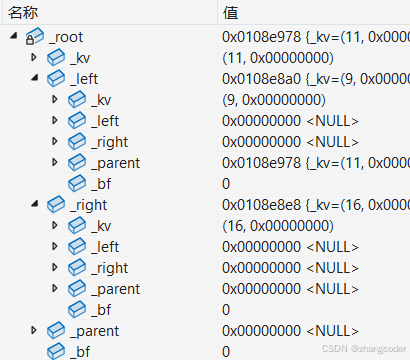
但3没有了!
添加这一行就能解决问题:
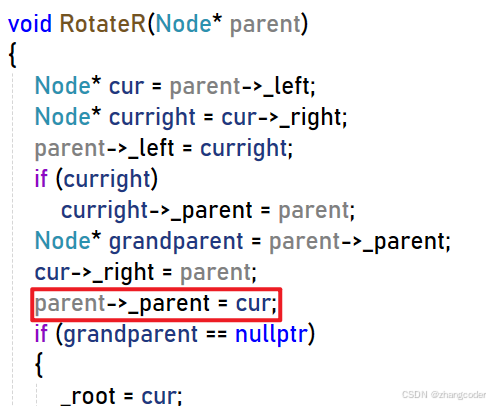
3.验证AVL树的方法
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此分两步:
1. 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中可能没有存储平衡因子的情况),节点的平衡因子是否计算正确