非常经典的回溯问题，运用的数学知识也很巧妙。
题目：
一个如下的 6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。
上面的布局可以用序列 2 4 6 1 3 5 来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
输入格式
一行一个正整数 n，表示棋盘是 n×n 大小的。
输出格式
前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。
输入输出样例
输入 ：
6
输出 ：
2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 4
题目分析：
初看题目会非常容易想到通过穷举的方式，在合适的位置对大棋盘这个二维数组标记行、列、斜线，通过递归进行行的变化，并用一个一维数组存储所需要输出的位置。但在编写的过程中可以发现，标记过程是冗余的，例如坐标（0，0）会标记包括（0，2）在内的行，（1，0）在内的列，（1，1）、（2，2）在内的斜线，而显然，作为第二行可能的元素（1，2）也会重复标记这几个点，这不仅使算法显得冗余，也增大了操作的出错率。这时就有读者要问了，那有没有一种办法可以只标记一次呢？有的，兄弟，有的。这里就要用到我们敏锐的观察力了。
我们可以注意到，由于一行一列只会有这一个元素，而无论是不是穷举，我们都会通过行变换来推动循环，所以行值完全不用标记，默认有一个后立马进行下一次循环，可以把列标记情况和对角线标记情况单独用数组存储，通过一定的函数关系判断当前递归元素是否被标记，而这个重点就在于对角线的标记。从主对角线出发，我们可以看到（0，0）、（1，1）...（n，n），列减去行都为0，（1，0）、（2，1）...（n+1，n），列减去行都为1，（0，1）、（1，2）...（n，n+1），列减去行都为-1，以此类推，我们可以得到以下这张图：
如此一来，我们只要用一个一维数组就可以存储主对角线上的标记情况这个数组下标从0到2n-1，标记着行列差值从-n+1到n-1。同样的，我们还要用一个数组来保存反对角线，可以看到（0、0）列加上行都为0，（1，0）、（1，1），列加上行都为1 ...（n-1,n-1），列加上行都为2n-2，以此类推，我们可以得到以下这张图：
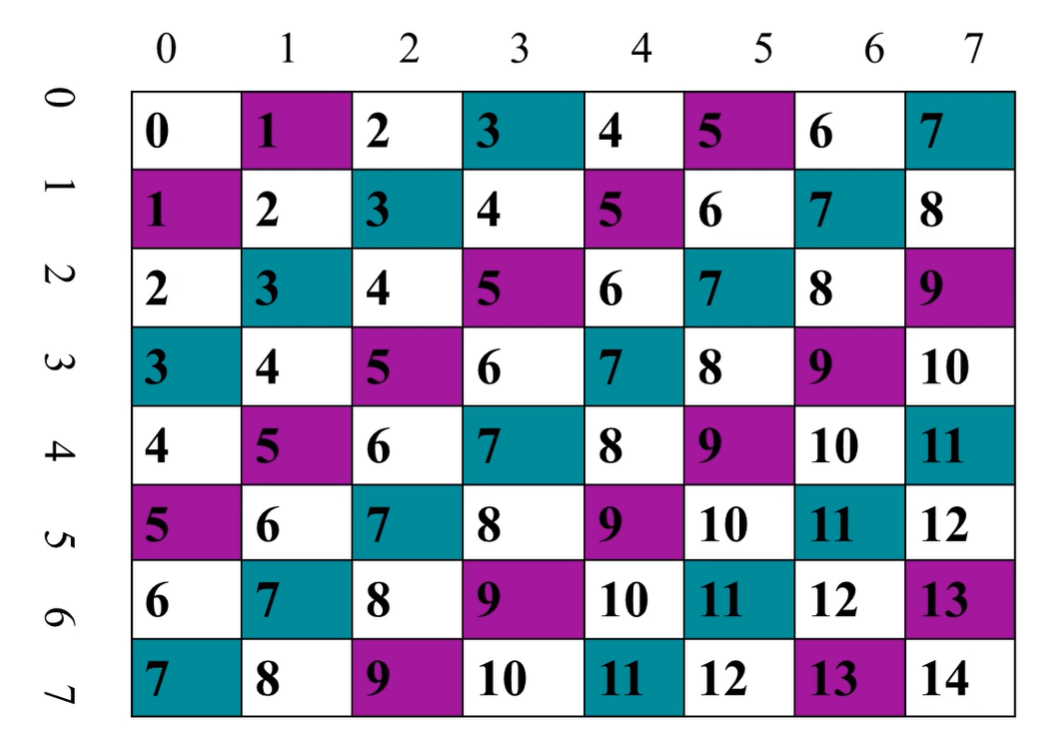图片来自经典算法-----八皇后问题（回溯算法）-CSDN博客
由此，我们可以得到，对于主对角线，我们有
f(x)=row-col+n-1 加上n-1是为了使结果作为下标不会成为负数
反对角线有
g(x)=row+col
其中row代表行值，col代表列值，n代表棋盘大小。
接下来就是代码问题，首先，我们要明白回溯的一个的核心就是“恢复”，代码形式类似：
HuiShuo(){代码A;代码B；代码C;HuiShuo();代码a;代码b；代码c;。。。
}
其中代码a、b、c是代码A、B、C的”返回“，如A为i++，则a为i--。以此达到“恢复”的作用。对于本题，则A、B、C很明显为对列、主对角线和反对角线的标记，a、b、c则为对其标记的“恢复”。我们通过递归实现行的变化，通过循环语句实现对列的变化，在遍历整个棋盘时，通过数组queen来记录棋子放置位置，下标为行坐标，内容为列坐标，如queen[2]=5，则该棋子在（2，5）的位置，每便利到最后一行并符合条件时，则视为一个方式，sum++，超过四条只计数不输出。
1 #include<stdio.h> 2 #include<stdlib.h> 3 4 int n; //棋盘大小 5 int sum; //方式总数 6 int* queen; //放置棋子 7 int* col; //列标记 8 int* dig1; //主对角线标记 9 int* dig2; //反对角线标记 10 11 void Queen(int row) { //row为行 12 if (row == n) { 13 sum++; 14 if (sum < 4) { 15 for (int i = 0; i < n; i++) { 16 printf("%d ", queen[i]+1); 17 } 18 printf("\n"); 19 } 20 } //递归到最后一行时说明存在放置方式，输出结果，超过四条不输出 21 for (int i = 0; i < n; i++) { 22 if (!col[i] && !dig1[row - i + n - 1] && !dig2[row + i]) { //列、主对角线、反对角线均未标记，则将该位置放置棋子，并递归 23 queen[row] = i; 24 col[i] = 1; 25 dig1[row - i + n - 1] = 1; 26 dig2[row + i] = 1; 27 28 Queen(++row); 29 row--; 30 col[i] = 0; 31 dig1[row - i + n - 1] = 0; 32 dig2[row + i] = 0; 33 } 34 35 } 36 } 37 38 int main() { 39 scanf("%d", &n); 40 queen = (int*)malloc(n * sizeof(int)); 41 col = (int*)calloc(n ,sizeof(int)); 42 dig1 = (int*)calloc(2*n , sizeof(int)); 43 dig2 = (int*)calloc(2*n , sizeof(int)); //初始化 44 Queen(0); 45 printf("%d", sum); 46 return 0; 47 }
运行通过！
