P9870 [NOIP2023] 双序列拓展
首先有一个暴力做法。
翻译一下题意,即为:

拓展也就是一个DP,我们设朴素DP,每次判断能否往下拓展,设fij表示x匹配到第i位,y匹配到第j位。
然后考虑特殊性质:
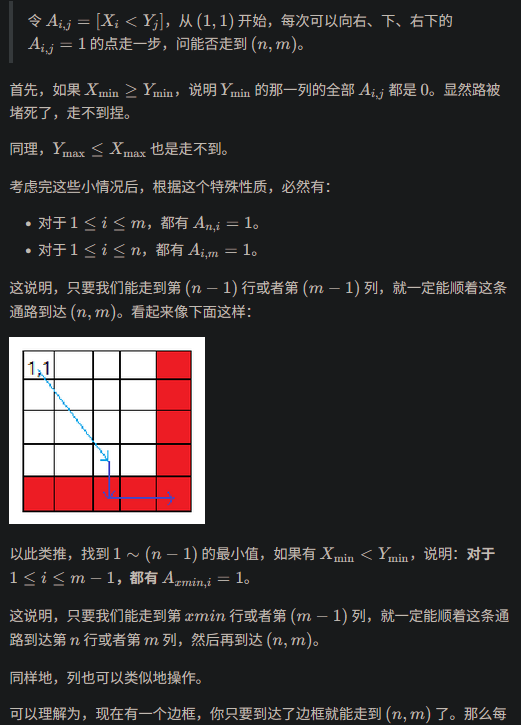
也就是说,这个特殊性质就是两个框往左上扫,扫到左上即可,

然后考虑正解,X最小值和Y最大值的位置不再固定,但是发现左上和右下可以独立考虑

#include <bits/stdc++.h>
using namespace std;const int N = 5e5 + 5;int f[N], g[N];struct Node {int min, max;Node(int ge = 0, int fe = 0) : min(ge), max(fe) {}
};Node preX[N], preY[N], sufX[N], sufY[N];inline Node update_node(int T[], const Node &p, int i) {return Node(T[i] < T[p.min] ? i : p.min, T[i] > T[p.max] ? i : p.max);
}bool check1(int x, int y, int n, int m) {if (x == 1 || y == 1) return true;Node X = preX[x - 1], Y = preY[y - 1];if (f[X.min] < g[Y.min]) return check1(X.min, y, n, m);if (g[Y.max] > f[X.max]) return check1(x, Y.max, n, m);return false;
}bool check2(int x, int y, int n, int m) {if (x == n || y == m) return true;Node X = sufX[x + 1], Y = sufY[y + 1];if (f[X.min] < g[Y.min]) return check2(X.min, y, n, m);if (g[Y.max] > f[X.max]) return check2(x, Y.max, n, m);return false;
}bool solve(int tmpf[], int tmpg[], int n, int m) {if (tmpf[1] >= tmpg[1]) return false;for (int i = 1; i <= n; i++) f[i] = tmpf[i];for (int i = 1; i <= m; i++) g[i] = tmpg[i];for (int i = 1; i <= n; i++)preX[i] = (i == 1) ? Node(1, 1) : update_node(f, preX[i - 1], i);for (int i = 1; i <= m; i++)preY[i] = (i == 1) ? Node(1, 1) : update_node(g, preY[i - 1], i);for (int i = n; i >= 1; i--)sufX[i] = (i == n) ? Node(n, n) : update_node(f, sufX[i + 1], i);for (int i = m; i >= 1; i--)sufY[i] = (i == m) ? Node(m, m) : update_node(g, sufY[i + 1], i);Node X = preX[n], Y = preY[m];if (f[X.min] >= g[Y.min] || g[Y.max] <= f[X.max]) return false;return check1(X.min, Y.max, n, m) && check2(X.min, Y.max, n, m);
}int tx[N], ty[N], ttx[N], tty[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int dummy, n, m, q;cin >> dummy >> n >> m >> q;for (int i = 1; i <= n; i++) cin >> tx[i];for (int i = 1; i <= m; i++) cin >> ty[i];cout << (solve(tx, ty, n, m) || solve(ty, tx, m, n) ? '1' : '0');while (q--) {for (int i = 1; i <= n; i++) ttx[i] = tx[i];for (int i = 1; i <= m; i++) tty[i] = ty[i];int cx, cy;cin >> cx >> cy;while (cx--) {int p, v;cin >> p >> v;ttx[p] = v;}while (cy--) {int p, v;cin >> p >> v;tty[p] = v;}cout << (solve(ttx, tty, n, m) || solve(tty, ttx, m, n) ? '1' : '0');}return 0;
}P6817 [PA 2013] Filary
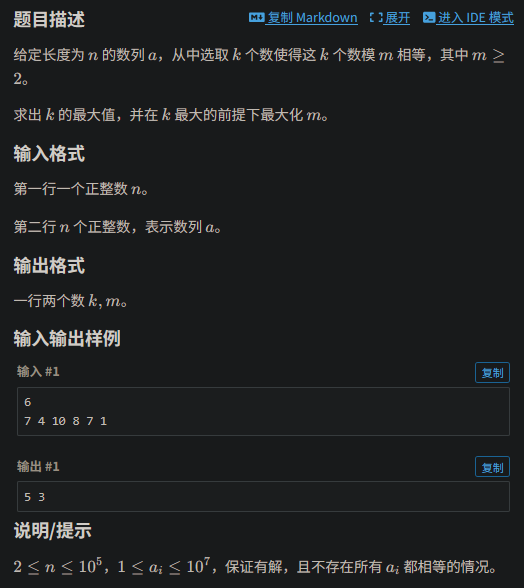
基础模拟赛有类似的题。
首先有一个性质,发现m=2时k是一定大于n/2的,所以答案下界是这个
所以任意一个数,在答案内的概率大于1/2
所以就随机选一个,其他数与他差分,我们要选尽可能多的数使它们的GCD大于1
直接枚举GCD不行。

这里写错了,是预处理最大质因子即可。
#include<bits/stdc++.h>
using namespace std;constexpr int maxn = 1e5+10, maxm = 1e7+10;
int n;
int a[maxn], b[maxn], pri[maxm], tot;
int lpf[maxm];
bool vis[maxm];
mt19937 rnd(114514);void getprime(int n){for(int i = 2;i <= n;i++){if(!vis[i]) pri[++tot] = i;for(int j = 1;j <= tot && i * pri[j] <= n;j++){vis[i * pri[j]] = true;if(i % pri[j] == 0) break;}}for(int i = 1;i <= tot;i++){for(int j = pri[i];j <= n;j += pri[i]) lpf[j] = pri[i];}
}pair<int,int> slove(){int pos = rnd() % n + 1;map<int,int> mp;for(int i = 1;i <= n;i++){b[i] = abs(a[i] - a[pos]);int c = b[i];while(c > 1){int d = lpf[c];mp[d]++;while(c % d == 0) c /= d;}}int mx = 0, ans = 0;for(auto [x, y] : mp) mx = max(mx,y);for(auto [x,y] : mp){if(y == mx){int res = 0;for(int i = 1;i <= n;i++){if(b[i] % x == 0) res = gcd(res,b[i]);}ans = max(ans,res);}}return{mx + count(b+1,b+n+1,0),ans};
}int main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n;for(int i = 1;i <= n;i++) cin>>a[i];getprime(*max_element(a + 1, a + n + 1));pair<int,int> res(0, 0);while((double)clock() / CLOCKS_PER_SEC < 1.3) res = max(res, slove());cout << res.first << ' ' << res.second << '\n';return 0;
}
P4757 [CERC2014] Parades

转移很奇怪的树形DP
首先设f[i]表示以i为根的子树的最优解。
根据这一类套路,肯定是DP过程中保存是否往父亲放边的。
首先有一个结论,就是如果根是关键点,根往儿子连边(牺牲一条u-son)一定不劣于牺牲两条u-son,匹配儿子的两个线头的。
所以DP时维护un[son][i]表示儿子son当前网上接的第i个线头。
然后DP时先优先匹配root和一个带线头的儿子,然后把儿子子树的线头都清理掉(因为已经用掉了)
然后考虑其他儿子,很难DP,考虑状压。
先预处理link[x][y]=true/false表示儿子x和y是否有连边。
然后直接状压DP。
#include <bits/stdc++.h>
using namespace std;const int N = 1010;
const int D = 15;int T, n, m;
int dp[N];
int f[1<<D];
int cnt, head[N], nxt[N<<1], to[N<<1];
bool vis[N][N];
vector<int> un[N]; int parentArr[N], depthArr[N], sz[N], heavy[N], top[N], dfn[N], rnkNode[N], timerHLD;int lowbit(int x) { return x & -x; }void init_all() {cnt = 0;memset(head, 0, sizeof(head));memset(vis, 0, sizeof(vis));memset(dp, 0, sizeof(dp));timerHLD = 0;for (int i = 0; i < N; ++i) {parentArr[i] = depthArr[i] = sz[i] = heavy[i] = top[i] = dfn[i] = rnkNode[i] = 0;heavy[i] = -1;}
}void adde(int u, int v) {to[++cnt] = v;nxt[cnt] = head[u];head[u] = cnt;
}void hld_dfs1(int u, int fa) {parentArr[u] = fa;depthArr[u] = (fa ? depthArr[fa] + 1 : 0);sz[u] = 1;int maxsz = 0;for (int e = head[u]; e; e = nxt[e]) {int v = to[e];if (v == fa) continue;hld_dfs1(v, u);sz[u] += sz[v];if (sz[v] > maxsz) {maxsz = sz[v];heavy[u] = v;}}
}void hld_dfs2(int u, int topf) {top[u] = topf;dfn[u] = ++timerHLD;rnkNode[timerHLD] = u;if (heavy[u] != -1) {hld_dfs2(heavy[u], topf);}for (int e = head[u]; e; e = nxt[e]) {int v = to[e];if (v == parentArr[u] || v == heavy[u]) continue;hld_dfs2(v, v);}
}int lca(int a, int b) {while (top[a] != top[b]) {if (depthArr[top[a]] < depthArr[top[b]]) swap(a, b);a = parentArr[top[a]];}return depthArr[a] < depthArr[b] ? a : b;
}void solve_dfs(int u, int fa) {int son[D], tot = 0;for (int e = head[u]; e; e = nxt[e]) {int v = to[e];if (v == fa) continue;solve_dfs(v, u);dp[u] += dp[v]; if (tot < D) son[tot++] = v; }for (int i = 0; i < tot; ++i) {int ch = son[i];for (int j = 0; j < (int)un[ch].size(); ++j) {int x = un[ch][j];if (vis[x][u]) {dp[u]++; un[ch].clear(); break; }}}static bool link[D][D];for (int i = 0; i < tot; ++i)for (int j = 0; j < tot; ++j)link[i][j] = false;for (int i = 0; i < tot; ++i) {for (int j = i + 1; j < tot; ++j) {int a = son[i], b = son[j];bool found = false;for (int p = 0; p < (int)un[a].size(); ++p) {for (int q = 0; q < (int)un[b].size(); ++q) {if (vis[un[a][p]][un[b][q]]) {link[i][j] = link[j][i] = true;found = true;break;}}if (found) break;}}}int maxMask = (1 << tot) - 1;f[0] = 0;for (int mask = 1; mask <= maxMask; ++mask) {f[mask] = f[mask & (mask - 1)];int a = __builtin_ctz(mask);for (int b = a + 1; b < tot; ++b) {if ( ((mask >> b) & 1) && link[a][b] ) {int newmask = mask ^ (1<<a) ^ (1<<b);f[mask] = max(f[mask], f[newmask] + 1);}}}dp[u] += f[maxMask]; un[u].clear();un[u].push_back(u);for (int i = 0; i < tot; ++i) {if (f[maxMask] == f[maxMask ^ (1<<i)]) {for (int x : un[son[i]]) un[u].push_back(x);}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cin >> T;while (T--) {init_all();cin >> n;for (int i = 1; i <= n; ++i) un[i].clear();for (int i = 1; i < n; ++i) {int u, v;cin >> u >> v;adde(u, v);adde(v, u);}hld_dfs1(1, 0);hld_dfs2(1, 1);cin >> m;for (int i = 0; i < m; ++i) {int u, v;cin >> u >> v;vis[u][v] = vis[v][u] = true;}solve_dfs(1, 0);cout << dp[1] << '\n';}return 0;
}
