牛牛题。
题意:给出两个排列 \(p,q\),要求构造一种路径方案,\((1,i)\rightarrow(n,p_i)\),\((i,1) \rightarrow(q_i, n)\),要求经过次数最大的边经过次数最少。
做法:
首先 \(p_i=i,q_i=i\) 直接就是 \(1\),轻松构造。
然后我们就啥也不会了,用 flow 之类的操作也没啥办法,看看 tag 只有一个 constructive,*3500,太困难了。然后点开题解。
发现除了上述情况外,答案至多是等于 \(2\) 的。至于为什么,不大于二可以通过下面的构造得出,这里先证明为什么不能是 \(1\)。
考虑假设只有 \(1\)。我们考虑对于 \(x=i\) 这一条直线到 \(x=i+1\) 这一条直线,如果不变那么没问题,但是如果是从排列 \(A\) 变成排列 \(B\),有一部分是在 \(x=i\) 这里动一下,然后走中间的横边,再在 \(x=i+1\) 排序一下。但是在 \(x=i\) 这里一定就得排成一个排列,要不然就会出现两个点一起走,但是这样就一定存在一条 \(x=i/i+1\) 上的边被交两次了,所以一定答案至少为 \(2\)。
那么现在我们知道答案是 \(2\) 考虑如何构造。我们不妨考虑先构造出一种通解,其他的在通解的基础上去调整。那当 \(p_i=n-i+1,q_i=n-i+1\) 的时候,感性理解,这样是交叉最多的,并且我们可以说明确实是可以通过这样的情况去构造出其他的解,我们先解释如何构造这种情况的解法。
发现这种情况非常可以递归构造,我们就把 \(1,n\) 的位置拉出来,考虑 \((1,1)\rightarrow(n,n)\) 属于 \(p,q\) 的分别从上面、右边和左侧、下面这两条路径走过,\((1,n)\rightarrow(n,1)\) 同样,这样刚好都是走两遍,并且不影响 \(n-2\) 的构造,只要我们先越过去即可。
给出一个 \(n=6\) 的构造:
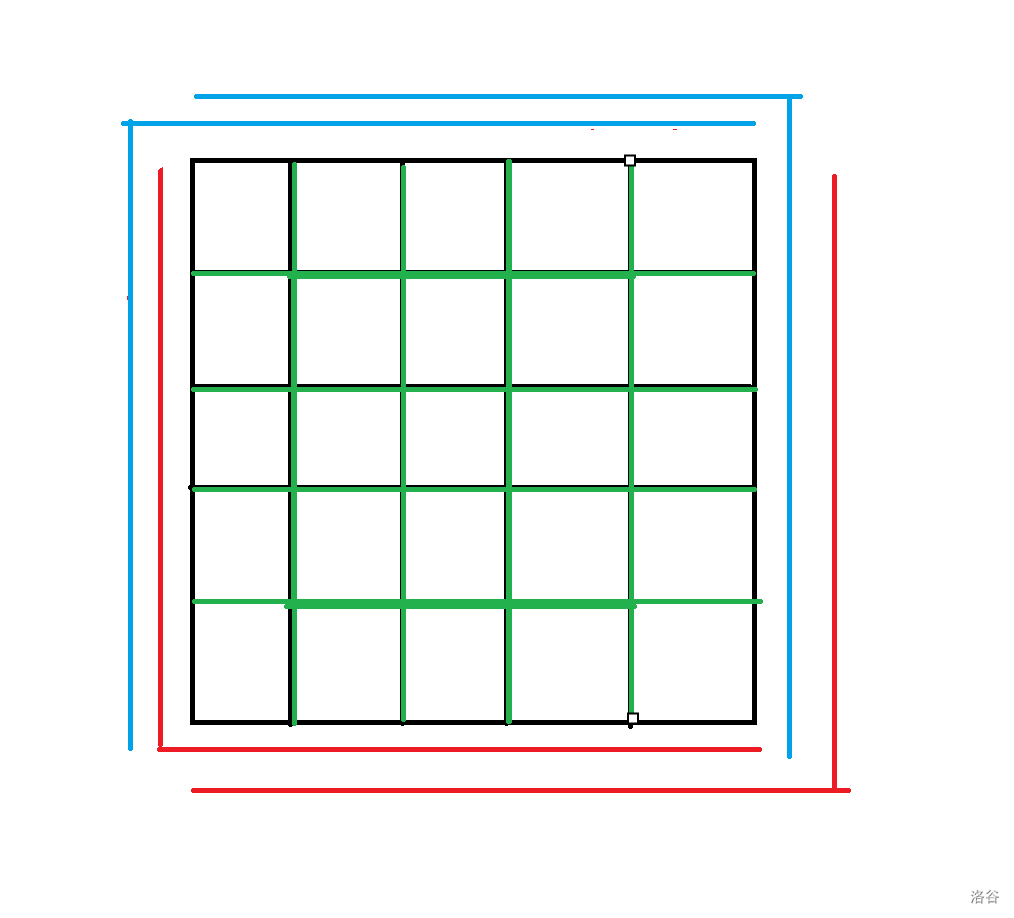
如图,红色和蓝色是最外圈的构造,中间的未处理的就递归地到绿色的部分转移到 \(n=4\) 的构造。
那么怎么对所有的进行构造呢?我们注意到 \(i<j,p_i>p_j\) 时两条路径一定有交点。从后往前匹配,考虑如果现在要 \(p_i=x\),那么我们就让前面的 \(x\) 一路往后换,在两条路径的第一个交点交换即可,因为观察到数组一直保持降序,所以一直都是有交点的。
按照上述过程构造即可
