| 题目 | 假期计划 | 策略游戏 | 星战 | 数据传输 |
|---|---|---|---|---|
| 算法概览 | \(贪心,bfs\) | \(线段树, ST表\) | \(哈希(和哈希),图论\) | \(倍增,动态 dp ,矩阵乘法\) |
| 难度 | \(\color{skyblue} 『提高+/省选-』\) | \(\color{lightgreen} 『普及+/提高』\) | \(\color{violet} 『省选/NOI-』\) | \(\color{violet} 『省选/NOI-』\) |
T1 假期计划
大意
给你一张\(n\) 个点, \(m\) 条边的无向图,每个点 (除了1号点) 有一个点权 \(val_i\) , 给定一个数 \(k\)
我们选定四个不同点 \(a, b, c, d\) ,使得 \((1, a), (a, b), (b, c), (c, d), (d, 1)\) 五组点对内两点之间的最短路经过不超过\(k + 1\) 条边
求出\(val_a + val_b + val_c + val_d\) 的最大可能值
\(1\leq n\leq 2500, 1\leq m\leq 10000, 1\leq k \leq 100, 1\leq val_i\leq 10^{18}\)
Sol
首先不必多说,肯定要对每个点跑一遍 \(bfs\) 来统计哪些点和它能够在一次操作内到达
然后我们先想一个极其暴力的暴力
因为路径内关键点只有四个,所以我们可以往暴力枚举这边去想
我们可以 \(O(n^4)\) 枚举 \(a, b, c, d\) 都是谁,正确性显然
但是这显然是做不过去的,考虑优化枚举
假设我们现在已经枚举了 \(a, b, c\) 三个点了,那么我们如何依据这个来缩小\(d\) 的枚举范围呢?
显然一个点要作为 \(d\) 的必要条件就是它得满足同时和\(1\), \(c\) 联通,这些点我们可以 \(O(n)\) 查询出来,换成预处理就是 \(n ^ 2\) 的
显然,在枚举的时候我们枚举点权最大的三个就可以了,具体为什么请读者思考
这样整体复杂度就降低到了 \(O(n ^ 3)\),还是过不去
那么同理,我们考虑优化 \(a\) 的枚举,和 \(d\) 一样,也是可以 \(n ^ 2\) 做出来,同样也是枚举前三个
其实枚举前三个就是维护最大的三个,最后 \(n ^ 2\) 枚举 \(b, c\) , 此时枚举\(a, d\) 就是常数级别的,可以通过
Code
// Problem: P8817 [CSP-S 2022] 假期计划
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8817
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Author: Floyd.Uranus
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int N = 2510;#define Floyd main
#define push_back emplace_backll inline read() {ll x = 0, f = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') f = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar ();}return x * f;
}void inline write (ll x) {if (x < 0) putchar ('-'), x = -x;if (x > 9) write (x / 10);putchar (x % 10 + '0');return void ();
}int n, m, k, fir[N][3];
bool flag[N][N], tag[N];
// flag[i][j] 表示我们从i可以一步走到j(反向相同)
// fir[i][0], fir[i][1], fir[i][2] 维护与i联通的前三大编号ll v[N], ans = 0;vector <int> e[N];void inline bfs (int st) {queue <int> x, step;x.push(st), step.push(0);while (x.size()) {int now = x.front(), a = step.front();x.pop(), step.pop();if (a == k + 1) continue;for (auto nxt : e[now]) {if (flag[st][nxt]) continue;flag[st][nxt] = 1, x.push(nxt), step.push(a + 1);}}return void();
}
//bfs标记void inline solve () {n = read(), m = read(), k = read();v[0] = -9e18;for (int i = 2; i <= n; ++i) v[i] = read();for (int i = 1; i <= m; ++i) {int a = read(), b = read();e[a].push_back(b), e[b].push_back(a);}for (int i = 2; i <= n; ++i) bfs (i);for (int i = 2; i <= n; ++i) {if (!flag[i][1]) continue;for (int j = 2; j <= n; ++j) {if (i == j || ! flag[i][j]) continue;if (v[i] > v[fir[j][0]]) fir[j][2] = fir[j][1], fir[j][1] = fir[j][0], fir[j][0] = i;else if (v[i] > v[fir[j][1]])fir[j][2] = fir[j][1], fir[j][1] = i;else if (v[i] > v[fir[j][2]])fir[j][2] = i;}}//预处理前三大for (int i = 2; i <= n; ++i)for (int j = 2; j <= n; ++j) {bool tf = 0;if (i == j || !flag[i][j]) continue;for (int i1 = 0; i1 < 3; ++i1) {if (fir[i][i1] == j) continue;if (fir[i][i1] == 0) break; //小优化,如果与i联通的不足3个点就break掉,下面f[j][j1] == 0 同理for (int j1 = 0; j1 < 3; ++j1) {if (fir[j][j1] == fir[i][i1] || fir[j][j1] == i) continue;if (fir[j][j1] == 0) {tf = 1;break;}ans = max (ans, v[i] + v[j] + v[fir[i][i1]] + v[fir[j][j1]]);tf = 1;//如果匹配过了就break,因为我们从大往小枚举虽然不一定最优,但是我们后面相同的方案还会反方向统计到,正好弥补了这种小概率错误break;}if (tf) break;}}write (ans);//暴力枚举b, c统计答案return void ();
}signed Floyd() {int TIMES = 1;while (TIMES --) solve ();return 0;
}
这道题比较考验思路的灵活性,说实话有点难
但是如果你刚开始没有想偏的话还是比较显然的
T2 策略游戏
大意
给你长度为 \(n\) 的 \(a\) 数组,长度为 \(m\) 的 \(b\) 数组,\(q\) 次询问,每次给出 \(l_1, r_1, l_2, r_2\) ,有两个人\(A, B\)来分别选择 \(a_{l_1}, a_{l_1 + 1},......, a_{r_1}\)中的一个数和 \(b_{l_2}, b_{l_2 + 1},......,b_{r_2}\)中的一个数,\(A\) 先选,\(A\) 要使选出的两个数乘积尽可能大,\(B\) 则想尽可能小,问在两人都最优决策下,乘积为多少?
\(1\leq n, m\leq 10^5, -10^9\leq a_i, b_i\leq 10^9\)
Sol
这道题就不想那么多部分分了,我们直接分类讨论即可
先把 \(0\) 拉出来单独考虑:
如果 \(A\) 有 \(0\) 的话,什么情况下他会用这个 \(0\) 作为答案呢?
显然,是当他没有其他数可选或者是无论选什么数 \(B\) 都能使乘积\(< 0\) 的时候
同理我们可以得到 \(B\) 的情况也是类似的,也就是 \(A\)存在一种选择使得 \(B\) 无论选什么数乘积都为正的时候
于是我们就有了以下式子
然后我们把这东西扔到最后去判断即可,先看其他情况(假设都没有\(0\))
我们现在定义 \(S_1, S_2\) 分别为 \(A, B\) 可选数集合,定义函数 \(f(S) = (0/1, 0/ 1)\) 表示\(S\) 内 有/没有 正数,有/没有 负数
然后开始大分讨
-
\(f(S_2) = (1, 1)\)
此时无论我们的 \(A\) 如何选择,答案都一定为负数,那么 \(A\) 一定是选择负数最大值或正数最小值,相应的, \(B\) 一定选正数最大值或负数最小值,我们将两种选择中较大的赋值给 \(ans\) 即可
-
\(f(S_2) = (1, 0)\)
此时我们发现 \(B\) 只能选正数,那么如果 \(A\) 有 正数的话,\(A\) 一定选择正数最大值,\(B\) 则选择正数最小值; 但如果 \(A\) 只有负数的话,\(A\) 一定选负数最大值,\(B\)一定选正数最大值。这两个结论显然
-
\(f(S_2) = (0, 1)\)
与第二种情况同理,这里不再赘述,请读者自证
-
\(f(s_2) = (0,0)\)
只能选 \(0\), 答案固定
然后我们就讨论完了,这里我们发现需要对 \(a, b\) 两个数组分别维护 正数最大值,负数最大值,正数最小值,负数最小值以及 \(0\) 的个数,区间询问, 这东西显然可以用 \(ST\) 表或者线段树做, 这里我用的是线段树写法(封装)
Code
// Problem: P8818 [CSP-S 2022] 策略游戏
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8818
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Author: Floyd.Uranus
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int N = 1e5 + 10, mod = 1e9 + 7;#define Floyd mainint inline read() {int x = 0, f = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') f = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar ();}return x * f;
}void inline write (ll x) {if (x < 0) putchar ('-'), x = -x;if (x > 9) write (x / 10);putchar (x % 10 + '0');return void ();
}
//快读快写,⚠️注意long long!!!int n, m, q, a[N][2], l1, l2, r1, r2;
ll ans;
//为了写的稍稍简洁(其实是为了封装),这里直接把a,b合成了一个二维数组 _(-_-)_struct node {int minn1, minn2, maxx1, maxx2;bool tag1, tag2, tag3;//tag1, minn1, maxx1 ---> 正数//tag2, minn2, maxx2 ---> 负数//tag3 ---> 0inline node () {minn1 = minn2 = 2e9, maxx1 = maxx2 = -2e9, tag1 = tag2 = tag3 = 0;}//初始化void merge (node a, node b) {minn1 = min (a.minn1, b.minn1);minn2 = min (a.minn2, b.minn2);maxx1 = max (a.maxx1, b.maxx1);maxx2 = max (a.maxx2, b.maxx2);tag1 = a.tag1 | b.tag1;tag2 = a.tag2 | b.tag2;tag3 = a.tag3 | b.tag3;return void();}//线段树两个节点的合并
};struct Segment_tree {#define mid ((l + r) >> 1)#define ls (x << 1)#define rs (x << 1 | 1)node t[N * 4];void inline build (int x, int l, int r, int fl) {if (l == r) {if (a[l][fl] > 0) t[x].tag1 = 1, t[x].maxx1 = a[l][fl], t[x].minn1 = a[l][fl];if (a[l][fl] < 0) t[x].tag2 = 1, t[x].maxx2 = a[l][fl], t[x].minn2 = a[l][fl];if (a[l][fl] == 0) t[x].tag3 = 1;return void();}build (ls, l, mid, fl);build (rs, mid + 1, r, fl);t[x].merge (t[ls], t[rs]);return void ();}node inline query (int x, int l, int r, int ql, int qr) {if (ql <= l && r <= qr) return t[x];node ret;if (ql <= mid) ret.merge (ret, query (ls, l, mid, ql, qr));if (qr > mid) ret.merge (ret, query (rs, mid + 1, r, ql, qr));return ret;}#undef mid#undef ls#undef rs
}A, B;
//封装, A, B分别对应 a, b数组void solve () {n = read(), m = read(), q = read();for (int i = 1; i <= n; ++i) a[i][0] = read();for (int i = 1; i <= m; ++i) a[i][1] = read();A.build (1, 1, n, 0), B.build (1, 1, m, 1);//建树for (int i = 1; i <= q; ++i) {l1 = read(), r1 = read(), l2 = read(), r2 = read();node ans1 = A.query (1, 1, n, l1, r1), ans2 = B.query (1, 1, m, l2, r2);// ans1, ans2 分别表示两个区间的具体数据if (ans1.tag2 && ans1.tag1) {if (ans2.tag1 && ans2.tag2)ans = max (1ll * ans1.minn1 * ans2.minn2, 1ll * ans1.maxx2 * ans2.maxx1);else if (!ans2.tag1)ans = (1ll * ans1.minn2 * ans2.maxx2);else if (!ans2.tag2)ans = (1ll * ans1.maxx1 * ans2.minn1);else ans = 0;}if (ans1.tag1 && !ans1.tag2) {if (ans2.tag2) ans = 1ll * ans1.minn1 * ans2.minn2;else if (ans2.tag1) ans = 1ll * ans1.maxx1 * ans2.minn1;else ans = 0;}if (!ans1.tag1 && ans1.tag1) {if (ans2.tag1) ans = 1ll * ans1.maxx2 * ans2.maxx1;else if (ans2.tag2) ans = 1ll * ans1.minn2 * ans2.maxx2;else ans = 0;}if (!ans1.tag1 && !ans1.tag2) ans = 0;if (ans1.tag3) ans = max (ans, 0ll);if (ans2.tag3) ans = min (ans, 0ll);/*Emmm....这里我是按照A的选择进行分类讨论的实质上和我上面说的一样读者可以自行思考😎*/write (ans), putchar ('\n');}return void ();
}signed Floyd() {int TIMES = 1;while (TIMES --) solve ();return 0;
}
这道题倒是没什么思维难度,题面也十分简洁,就是要注意分类讨论的细节,而且维护的值比较多,稍微难写,一不注意就写了150多行
T3 星战
不可以,总司令!
没错就是这个梗的出处 (偷笑🤭)
大意
给你 \(n\) 个点, \(m\) 条有向边,\(q\) 次操作
操作共分为 \(4\) 种
-
删除边 \(u, v\)
-
删除以 \(u\) 为终点的所有边
-
添加边 \(u, v\)
-
将以 \(u\) 为终点的所有边全部加回来
其中每个边都一定是 \(m\) 条有向边里原有的
每个操作后,我们要判断以下条件,满足输出 YES, 不满足输出 NO
\(1\leq n, m, q\leq 5\times 10^5\)
Sol
所以说全部输出 NO 可以骗取大量分数是有道理的,在数据非刻意构造的情况下这条件还真难满足
当然暴力是好写的,分也是少的可怜的,这里我就不再说其他推导了,直接正解
我们考虑我们并不在意边的状况,我们只是在意 每个点的出度是否为 \(1\),而且我们甚至连是否能进入一个环都不用管,因为如果出度都为 \(1\) 的话,必定满足第二个条件(读者自证)
那么也就是说,最后每个点的出度状况是确定的(废话)
于是我们就有了暴力统计出度的做法, 复杂度 \(O(q\times (n + m))\)
对于题目中给出的 \(4\) 种操作, \(2, 4\) 我们直接统计出度的算法是很劣的,但是统计入度却是好做的,那么我们该如何把出度转移到入度上统计呢?
显然我们只能统计入度之和,如果只是单纯的 \(+1,-1\) ,正确性显然是错的
那么我们就来到了哈希部分
对于每一个数我们可以给它随机赋上一个映射值 \(val_i\) ,把操作入度统计时每次 \(now_v ++\) 改成 \(now_v += val_u\) 即可,记录所有点出度均为 \(1\) 时的和为 \(sum\)
我们容易想到,这样子的话我们每一个出度的映射值大概率是唯一的,统计时不同状况和也是大概率唯一的 (除非你运气真的太"好"了)
那么我们直接每次判断\(\sum\limits_{i = 1}^n now_i\) 是否等于 \(sum\) 即可
然后就做完了
Code
// Problem: P8819 [CSP-S 2022] 星战
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8819
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Author: Floyd.Uranus
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int N =1e6 + 10;
const ll mod = 1e9 + 7;#define Floyd mainll inline read () {ll x = 0, f = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') f = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar ();}return x * f;
}void inline write (ll x) {if (x < 0) putchar ('-'), x = -x;if (x > 9) write (x / 10);putchar (x % 10 + '0');return void ();
}int n, m, q, ind[N];
ll sum = 0, ans = 0, to[N], g[N], now[N];void inline solve () {srand (time (0));n = read(), m = read();for (int i = 1; i <= n; ++i){to[i] = (rand() * 1ll * rand() * rand() * rand() % mod), sum += to[i];//这里我赋值的映射范围是1~1e9 + 7, 很多数都相同的概率较低,可以放心哈希}for (int i = 1; i <= m; ++i) {int a = read(), b = read();g[b] += to[a];//g[i] 表示原图上i点用入度统计出度的哈希值之和}for (int i = 1; i <= n; ++i) {ans += g[i], now[i] = g[i];}q = read();for (int i = 1; i <= q; ++i) {int id = read(), u, v;if (id == 1) {u = read(), v = read();now[v] -= to[u], ans -= to[u];}if (id == 2) {v = read();ans -= now[v];now[v] = 0;}if (id == 3) {u = read(), v = read();now[v] += to[u], ans += to[u];}if (id == 4) {v = read();ans -= now[v], now[v] = g[v];ans += now[v];}if (ans == sum) puts("YES");else puts("NO");}return void ();
}signed Floyd() {int TIMES = 1;while (TIMES --) solve ();return 0;
}
不好想,如果考场上真做不出来的话, 这边建议您骗分呢亲
T4 数据传输
这也真是难写,反正赛场上是场切不了的
大意
给你一颗树,每个点都有点权 \(val_i\) ,现在给你 \(q\) 次询问,每次从点 \(s\) 出发,每次可以跳 \(1, 2, ..., k\) 步, 一直跳到 \(t\) ,问路径上你经过的点点权之和最少为多少?
这里先粘一下数据范围 QWQ
对于所有的测试数据,满足 \(1 \le n \le 2 \times {10}^5\),\(1 \le Q \le 2 \times {10}^5\),\(1 \le k \le 3\),\(1 \le a_i, b_i \le n\),\(1 \le s_i, t_i \le n\),\(s_i \ne t_i\)。
| 测试点 | \(n \le\) | \(Q \le\) | \(k =\) | 特殊性质 |
|---|---|---|---|---|
| \(1\) | \(10\) | \(10\) | \(2\) | 是 |
| \(2\) | \(10\) | \(10\) | \(3\) | 是 |
| \(3\) | \(200\) | \(200\) | \(2\) | 是 |
| \(4 \sim 5\) | \(200\) | \(200\) | \(3\) | 是 |
| \(6 \sim 7\) | \(2000\) | \(2000\) | \(1\) | 否 |
| \(8 \sim 9\) | \(2000\) | \(2000\) | \(2\) | 否 |
| \(10 \sim 11\) | \(2000\) | \(2000\) | \(3\) | 否 |
| \(12 \sim 13\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(1\) | 否 |
| \(14\) | \(5 \times {10}^4\) | \(5 \times {10}^4\) | \(2\) | 是 |
| \(15 \sim 16\) | \({10}^5\) | \({10}^5\) | \(2\) | 是 |
| \(17 \sim 19\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(2\) | 否 |
| \(20\) | \(5 \times {10}^4\) | \(5 \times {10}^4\) | \(3\) | 是 |
| \(21 \sim 22\) | \({10}^5\) | \({10}^5\) | \(3\) | 是 |
| \(23 \sim 25\) | \(2 \times {10}^5\) | \(2 \times {10}^5\) | \(3\) | 否 |
特殊性质:保证 \(a_i = i + 1\),而 \(b_i\) 则从 \(1, 2, \ldots, i\) 中等概率选取。
Sol:
由于这道题难度较大且部分分和正解之间联系较大 (好题!),所以我将一个一个部分的讲解 (如果太简单除外)
Part 1 : k = 1 (16pts)
这里是显然的,在 \(k = 1\) 的情况下,我们的路径上每一个数都要选到,我们直接用倍增 \(LCA\) 维护即可
时间复杂度 \(O(q \log n)\)
Part 2 : k = 2 && \(n, q\leq 2000\) (32pts)
在这种情况下,我们可以考虑放弃 \(\log_2 (n)\) 的 \(LCA\) 求法,转而选择把路径上所有点 \(O(n)\) 取下来做一遍\(dp\), 这样我们就是在一个序列上的问题了,\(dp\) 转移方程是好写的
(这里要注意 \(i\) 不是原图中的编号,而是我们将路径取出后的节点编号)
时间复杂度 \(O(n\times q)\)
Part 3 : k = 3 && \(n, q\leq 2000\) (52pts)
和上面不同的就是,\(k\) 的取值变成了 \(3\)
那么我们还是像上面一样直接 \(dp\) 吗?
你大胆写了一发跟上面差不多的 \(dp\) , 然后就发现......你寄了
其实这两种情况是有本质差别的, 你可以考虑下面这张图
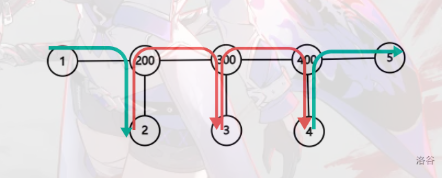
图中标注的线段为 \(k = 3\) 时的最优方案,而在 \(k = 2\) 时显然不会出现这种情况
也就是说,我们的最优路径可能不止经过两点之间简单路径上的点,还有可能包含某一个点的子节点
类似的,根据贪心,我们把路径上的点的点权最小的子节点纳入我们的考虑范围即可
我们可以设 \(f_{i, 0/1}\) 表示跳到了点 \(i\) 自己/它儿子的最小值,\(num_i\) 表示 \(i\) 号节点带来的需要考虑的子节点权值
聪明的你很快就想出了 \(dp\) 的状态转移方程
时间复杂度 \(O(n\times q)\)
Part 4 : 特殊性质 (76pts)
前面的都做完了,我们来看一下特殊性质
这相当于是随机生成一颗树,期望树高为 \(\log n\) 级别
也就是说,我们的 \(LCA\) 路径上经过的点也是期望 \(\log n\) 级别
这和前面的不是差不多吗?
然后我们也是暴力提取路径即可
复杂度 \(O(q \log n)\)
Part 5 : k = 2 (88pts)
做到这里就非常接近正解了
因为 \(k = 2\) ,这个转移方程是相当简单的,于是我们就可以考虑上矩阵乘法来优化
我们回顾一下,\(dp\) 方程是
我们可以转化为一个 \({min,+}\) 转移矩阵 \(A_i\), 初始矩阵为 \(st\), 答案矩阵为 \(ans\), 这些应该都是好推出来的
所以我们直接上矩阵乘法优化即可,用倍增 \(LCA\) 来维护
但是有一点要注意的我们的方程转移过程如下
也就是说,我们的倍增要维护两种,一种是从父节点往子节点乘,另一种反过来(拆成\(LCA\)两侧两段序列),毕竟矩阵乘法它不满足交换律,乘的时候必须有序
例如这张图,我们的询问是 \(4, 6\) ,矩阵乘法的转移如下
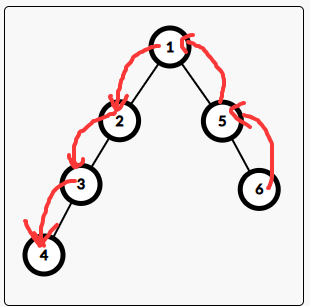
那么我们从 \(6\) 到 \(1\) 的路径就应该维护从下往上的乘积,\(1\) 到 \(4\) 反过来,而且要注意 \(4\) 的矩阵不能乘,这个由上面的式子可以推得
复杂度为 \(O(q\log n \times 2^3)\)
Part 6 : 正解 (100pts)
正解其实已经了然了
就是矩阵乘法倍增做一下 \(k = 3\) 的情况即可
但这样显然不行,复杂度 \(O(q\log n\times 5^3)\),单次转移都有 \(125\) 的常数,是我们接受不了的
怎么办呢?
考虑优化一下 \(dp\) 状态
我们敏锐的发现其实我们转移过程只牵扯到距离,于是我们就可以考虑用距离表示 \(dp\) 状态
考虑设 \(f_{i,0/1/2}\) 表示我们当前做到了 \(i\) 号点,转移到距离 \(i\) 号点距离为 \(0/1/2\) 的点的最小代价
显然最后的答案就是 \(f_{len,0}\)
转移方程其实并不难搞,分情况讨论可以得到
根据上面三个式子我们不难看出转移矩阵 \(A_i\) 是什么
初始矩阵也差不多,是 \(\begin{Bmatrix} val_i\\ \infty\\ \infty\end {Bmatrix}\)
细节和上面 \(k = 2\) 的情况差不多,整体复杂度为 \(O(q\log n\times 3^3)\)
码量比较大,细节较多,要想明白再写
Code
// Problem: P8820 [CSP-S 2022] 数据传输
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8820
// Memory Limit: 1024 MB
// Time Limit: 3000 ms
// Author: Floyd.Uranus
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
typedef long long ll;#define Floyd mainconst ll inf = 1e18;
constexpr int N = 2e5 + 10;int inline read() {int x = 0, f = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') f = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar ();}return x * f;
}void inline write (ll x) {if (x < 0) putchar ('-'), x = -x;if (x > 9) write (x / 10);putchar ('0' + x % 10);return void ();
}//注意long long !int len;struct square {ll node[3][3];//能少开尽量少开,不然小心MLE!inline square () {for (int i = 0; i < 3; ++i) for (int j = 0; j < 3; ++j)node[i][j] = inf;}//初始化要全部赋值为 infvoid inline readin () {for (int i = 0; i < 3; ++i)for (int j = 0; j < 3; ++j)node[i][j] = read();}void inline print () {puts("--------------------");for (int i = 0; i < len; ++i) {for (int j = 0; j < len; ++j)write (node[i][j]), putchar (' ');putchar ('\n');}puts("--------------------");}friend square operator *(square a, square b) {square c;for (int i = 0; i < len; ++i)for (int j = 0; j < len; ++j)for (int k = 0; k < len; ++k)c.node[i][j] = min (c.node[i][j], a.node[i][k] + b.node[k][j]);return c;}//矩阵乘法,len 为方阵的大小friend square operator +(square a, square b) {for (int i = 0; i < len; ++i)for (int j = 0; j < len; ++j)a.node[i][j] += b.node[i][j];return a;}void set_sample () {for (int i = 0; i < len; ++i) node[i][i] = 0;}//设置单位矩阵ll sum () {ll S = 0;for (int i = 0; i < len; ++i)for (int j = 0; j < len; ++j)S += node[i][j];return S;}//封装的 min,+ 矩阵乘法
}f[N][20], g[N][20];//这里我用f来记录从下往上乘的矩阵倍增,g是从上往下乘的矩阵倍增int n, m, k, fa[N][20], dep[N];
ll val[N], num[N];
vector <int> e[N];void inline dfs (int now, int fat) {num[now] = val[fat];fa[now][0] = fat, dep[now] = dep[fat] + 1;for (int i = 1; i < 20; ++i)fa[now][i] = fa[fa[now][i - 1]][i - 1];for (auto nxt : e[now]) {if (val[nxt] < num[now]) num[now] = val[nxt];//处理距离为1的点权最小值if (nxt == fat) continue;dfs (nxt, now);}return void ();
}void inline SET (int i) {/*理论上来说len == 1的时候可以直接维护和,但是为了统一这里设置了一个 边长为1 的方阵转移,本质上和直接维护和是一样的*/if (len == 1) f[i][0].node[0][0] = val[i];if (len == 2) {f[i][0].node[0][0] = val[i];f[i][0].node[0][1] = val[i];f[i][0].node[1][0] = 0;}//边长为2的方阵if (len == 3) {f[i][0].node[0][0] = val[i];f[i][0].node[0][1] = val[i];f[i][0].node[0][2] = val[i];f[i][0].node[1][0] = 0;f[i][0].node[1][1] = num[i];f[i][0].node[1][2] = num[i] + val[i];f[i][0].node[2][1] = 0; }//边长为3的方阵g[i][0] = f[i][0];return void ();
}inline int LCA (int a, int b) {if (dep[a] > dep[b]) swap (a, b);int dis = dep[b] - dep[a];for (int i = 0; i < 20; ++i)if ((dis & (1 << i))) b = fa[b][i];if (a == b) return a;for (int i = 19; i >= 0; --i)if (fa[a][i] != fa[b][i])a = fa[a][i], b = fa[b][i];return fa[a][0];//正常倍增LCA
}inline void get_ans (int lca, int a, int b) {square tmp1, tmp2, st;st.node[0][0] = val[a];//初始矩阵(因为其它位置全都是inf,所以没必要把长度和宽度更改)tmp1.set_sample (), tmp2.set_sample();//初始化为单位矩阵if (lca != a) {a = fa[a][0];int dis = dep[a] - dep[lca] + 1, now = a;//这里就是我说的a的转移矩阵不参与运算for (int i = 0; i < 20; ++i)if ((dis & (1 << i))) tmp1 = g[now][i] * tmp1, now = fa[now][i];//注意矩阵乘法的先后顺序}if (lca != b) {int dis = dep[b] - dep[lca], now = b;for (int i = 0; i < 20; ++i)if ((dis & (1 << i)))tmp2 = tmp2 * f[now][i], now = fa[now][i];//注意矩阵乘法的先后顺序}tmp1 = tmp2 * tmp1;st = tmp1 * st;write (st.node[0][0]);putchar ('\n');return void ();
}void inline solve () {n = read(), m = read(), k = read(), val[0] = 1e18, len = k;for (int i = 1; i <= n; ++i) val[i] = read();for (int i = 1; i < n; ++i) {int a = read(), b = read();e[a].push_back(b), e[b].push_back(a);}for (int i = 0; i < 20; ++i)f[0][i].set_sample(), g[0][i].set_sample();dfs (1, 0);for (int i = 1; i <= n; ++i) `SET (i);for (int i = 1; i < 20; ++i)for (int j = 1; j <= n; ++j)f[j][i] = f[j][i - 1] * f[fa[j][i - 1]][i - 1],//逆序乘,下面的矩阵放在前面的位置g[j][i] = g[fa[j][i - 1]][i - 1] * g[j][i - 1];//正序乘,上面的矩阵放在前面的位置for (int i = 1; i <= m; ++i) {int a = read(), b = read(), lca = LCA (a, b);// write (lca), putchar ('\n');get_ans (lca, a, b);}return void ();
}signed Floyd () {int TIMES = 1;while (TIMES --) solve ();return 0;
}
总而言之,这是一道好题!
好评!
对矩阵乘法不熟悉的家人们可以多学习一下 \(QWQ\)

 CSP-S 2022 题解报告
CSP-S 2022 题解报告