1. 历史背景和动机
计算机图形场景资产的转换仍然是一个重大问题,尤其是在表面外观方面。不同的渲染器和3D引擎使用不同的着色系统、着色语言以及固定渲染管线,这些系统不易互相操作。此外,准确建模表面外观仍然是一个复杂且紧迫的问题,并且是活跃的科学研究课题。尽管如此,如今从事基于物理的渲染(包括离线和实时渲染)的行业仍然迫切需要找到一个标准化的材质模型,以涵盖典型工作流程中最常见的用例。
多年来,随着不同供应商达成共识,将材质定义与场景中的光传输模拟分离,一些事实上的标准外观定义框架应运而生。这些通用框架包括 MaterialX [ Smythe 2016 ]、开放着色语言 (OSL) [ Gritz 2010 ] 和材质定义语言 (MDL) [ Kettner 2015 ],它们允许将材质指定为原始表面反射模型的组合。然而,仅靠这些框架不足以满足最终用户的外观开发需求,他们不应该为了日常任务而从头构建复杂的表面着色器。实际上,使用标准的“超级着色器”参数化方法会更加方便,即一个涵盖各种情况的单一整体材质定义,并具有一组定义明确的参数,可以进行调整以表示大多数现实世界(以及虚拟世界)的材质。
之前已经有过多种关于这种超级着色器的提案,例如 Disney 的 Principled Shader [ Burley2012 ]、Allegorithmic 的 PBR 着色模型 [ McDermott2018 ],以及最近的 Autodesk 标准表面着色器 [ Georgiev2019 ] 和 Adobe 标准材质 [ Kutz2021 ]。Autodesk 标准表面着色器的先行者为 Anders Langlands 的 alSurface [ Langlands2014 ] 和 Autodesk 3ds Max 的物理材质 [ Andersson2016 ] 。而 3ds Max 的物理材质又受到 Allegorithmic 模型、Disney 的 Principled Shader 以及多个实时 3D 引擎的行业通用趋势的强烈启发。
然而,这些模型都源自一家公司,主要是为了满足该公司特定软件产品和客户的需求而设计的。因此,需要制定一项由业内所有重要参与者共同协作制定的规范,使其成为一项开放标准,并具备足够的灵活性来适应整个行业的常见用例。它应该融合艺术家、软件开发人员和产品经理的经验,以了解哪些模型在生产中真正有用。为此,本规范中定义的模型由 Autodesk 和 Adobe 合作开发,并吸收了其他多个行业合作伙伴的意见。它是由美国学院软件基金会 (ASWF) 托管的一项开放标准。
OpenPBR 旨在成为产品之间的通用接口,同时也是一种实用且易于理解的接口,适用于大多数日常用例。对于它未涵盖的更专业的用例(例如非常高端的皮肤、头发、布料或体积着色),可能需要使用特定于渲染器的着色器,或构建定制的着色网络。我们的目标是使整体行为简单、合乎逻辑、直观且易于理解,以便用户能够轻松熟悉它,同时又能基于物理渲染。
因此,我们采用了一种特定形式的材料结构,该结构已被证明可作为媒体和娱乐领域的通用模型(图1)。该结构大致包括:
- 由金属或电介质混合制成的基底。该基底层的界面(电介质或金属)产生主镜面反射叶。电介质基底包含以下三种成分之一,这些成分在统计上可以混合 :
- 高光-漫反射:具有不透明内部介质的电介质,例如木材、花岗岩、混凝土、纸板和墙漆。
- 次表面散射:具有密集高度散射内部介质的电介质,例如塑料、大理石、皮肤、植被和食物。
- 半透明基底:具有半透明内部介质的电介质,例如玻璃、晶体和液体。
- 涂层:一层可选的介电层,可能含有吸收介质,作为基底顶部的涂层。该涂层的介电界面提供了次级镜面波瓣。
- 绒毛:可选层,代表其他所有物体之上的微纤维(如细毛、桃绒毛、纺织线和灰尘颗粒)的反射。
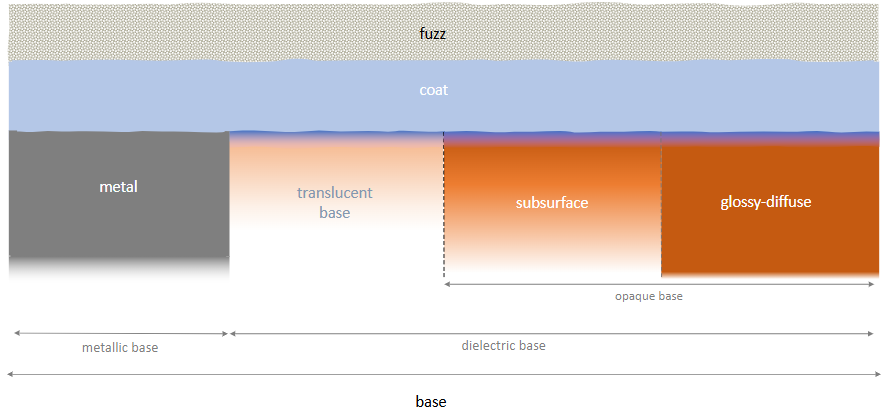
图 1:我们着色器建模的理想物理材质示意图。水平堆叠的层表示统计混合,垂直堆叠表示分层。
我们使用一种简单的公式来详细定义这种物理材质结构,该形式涉及通过分层和混合操作组成的材质层。这种公式足够通用,可以描述任意复杂的材质,但本文将其限制用于定义上述特定的材质结构。与之前的模型(例如 Autodesk Standard Surface [ Georgiev2019 ])不同,我们通过尽可能明确地描述物理结构来定义模型,而不是通过指定特定的实现形式。在计算机图形学层面,如果指定了每层间界面的 BSDF(双向散射分布函数)和每层内介质的体积特性,则该模型在物理上是完全指定的。然后将模型的真实外观定义为通过物理光通过组合层的整个结构所获得的 BSDF。因此,实现具有明确的目标外观,它们可以根据物理和光传输对其进行推理并在逻辑上以或多或少的保真度进行近似。实现越接近重现这种真实物理外观,就越符合规范。
对于结构的每个组合层,我们定义了一组直观的参数来控制底层的物理属性,并详细描述了如何根据这些参数确定这些属性。我们并非为所有可能的情况都提供参数,而是刻意将参数集精简为实际中最有用的参数。这些参数的设计不仅直观易懂,也确保用户尽可能在物理上可行的范围内操作。完整列表请参阅参数参考部分。
2. 公式
金属、玻璃或墙面涂料等基本材质表面的光散射特性已得到深入研究,并可通过简单的分析模型准确表示。其他材质,例如成品木材、布料或皮肤,由层叠的半透明物质层组成。此类材料更复杂的行为源于光在这些层间界面处散射并穿过这些层传播的结果。材质表面的性质也存在差异,例如,生锈的金属表面会存在裸露的镜面金属区域和暗淡的氧化铁区域,这些材质之间的过渡可能很突然,也可能是平滑的混合。
为了模拟此类材料,我们引入了一种简单的公式方法,它描述了一种由均匀电介质或导体层组成的抽象概念,这些层由定义明确的 BSDF 包围。对这些层进行分层和统计混合这两个基本操作,提供了一种用于构建定义明确的物理材质模型的公式化语言。
2.1 层
每层由均匀的电介质或导电介质组成在概念上水平方向无限大,垂直方向有限高,上方以具有给定界面 BSDF 的表面为界f因此,我们将一般平板表示如下:

其中,f为层间界面的BSDF,V的定义在下面。为了清楚地描述他们的关系,我们画了如下图所示的层示意图。

我们在二维表面的局部空间中工作,因此水平方向指的是局部平面内的方向,垂直方向指的是与向外的着色法线对齐。朝向材质顶部的方向被理解为与当前光传输顶点处的局部着色法线对齐。为了使光传输易于处理,我们假设在结构中层深度的微观尺度上,层是局部均匀的。在更大的宏观尺度上,层的属性以及材质的整体结构会随着表面的变化而变化。我们不规定如何在微观层面上物理描述层表面,但在微观层描述层面,它们是具有已知 BSDF 的平坦界面。我们将尽可能具体地说明所选 BSDF 的函数形式,但在大多数情况下,我们会参考文献来了解完整的实现细节。BSDF 大多是微平面模型(除了源自微薄片理论的fuzz BSDF)。
每个BSDF都是输入和输出方向的函数 \(f(\omega_i, \omega_o)\),其中,按照通常的惯例,这两个方向都指向远离表面顶点的位置,\(\omega_o\) 在出射光的方向上,而$\omega_i $ 与入射光的方向相反。从物理上讲,BSDF应该具有能量守恒和互易性。BRDF¹ \(f(\omega_i, \omega_o)\) 的能量守恒相当于要求定向反射率(或反照率) \(E(\omega_o) \leq 1\) 对于所有输出射线方向,其中 \(E(\omega_o)\) 被定义为BRDF在与 \(\omega_o\) 相同的半球 \(H_+\) 上方向的积分,使用投影立体角度量:
更一般地,对于透射BSDF,有一个类似的约束 \(E(\omega_o) + T(\omega_o) \leq 1\),其中定向透射率\(T(\omega_o)\) 通过将BSDF积分到与 $\omega_o $ 相反的半球 \(H_-\) 来定义。所有使用的BSDF在此意义上都是能量守恒的。此外,一个不耗散任何能量的BSDF,例如电介质界面或具有白色反照率的漫反射表面,被称为能量保持的,并满足 \(E(\omega_o) + T(\omega_o) = 1\)。 互易性是 BSDF 在参数交换下对称的要求,即 \(\omega_i \leftrightarrow \omega_o\)。在某些情况下,这会被放宽,使用非互易 BSDF 以求简单或高效,因为在实践中它不会导致严重问题。
如果层完全不透明(例如,导电或漫反射),我们只需指定表面 BSDF \(f\),因为内部介质对光传输无关紧要。如果层是非不透明的,即半透明的,则层内部介质 \(V\) 被视为均匀介电质,其中可选地包含指定的均匀体积介质(或“VDF”)。VDF 指定义体积光学介质的一组量(一般为空间变化的场),即:
• 归一化相函数参数
• 吸收和散射系数(或者,消光系数和散射反照率)
• 嵌入介电介质的折射率 (IOR) 和色散
我们假设渲染器知道体积属性可能从点到点变化,从表面参数继承而来,以及这些场如何在包围表面的空间中“填充”是一个实现问题。
介质 (V) 要么指定其自身深度,要么是结构底部的半无限“体”体积介质。我们将这种概念上向下无界的体介质表示为 \(V^\infty\)。当然,这是一种抽象,我们理解这种半无限介质实际上只是代表局部表面结构的底层。介质很可能在某处终止,但远离表面,在微观尺度上。请注意,有限深度层 \(S\) 的底部界面的 BSDF 不需要指定,因为它可以从底层的 BSDF 与 \(S\) 介质的属性组合中推导得出(正如在分层部分中讨论的)。
如果层的边界 BSDF 完全非透射且不透明(例如,金属或漫反射),则内部介质对光传输目的无关紧要。为方便起见,可以省略它。
不透明材质定义为 \(S_{\text{opaque}} = \text{Slab}(f)\)。
材质结构底部的半无限层用一个块状介质 \(V^\infty\) 表示,该介质没有底部界面:
为完整起见,层的缺失(即没有表面或底层介质),这仅对应于环境介电介质,用 \(\text{Slab}(\emptyset)\) 表示。
层本身并不指定与其他层相关的任何信息(例如,其基底层或覆盖层)。层上方和下方的相邻介质将取决于它在最终层结构中的位置。整个结构最顶部的环境介电介质(如果为薄壁,则包括底部)也被假设为已给定且未由模型指定。如果渲染器跟踪表面嵌入的介电介质(通过诸如“嵌套介电体”[Budg2002]的方案),这可能是场景中某些透明物体的内部介电块体,例如一块玻璃或水体,那么周围的环境介质就是一个介电体,其折射率(IOR)我们记为 \(n_{\text{ambient}}\),或者如果没有进行介电介质跟踪,则 \(n_{\text{ambient}}\) 可以假设为 1,对应于空气或真空。
给定组成层,我们然后通过“垂直”层叠和“水平”混合层来构建更复杂的复合材质,如下所述。
2.2 分层
分层操作通过将一块板材 $ S_{\text{coat}}=\text{Slab}(f_{\text{coat}},V_{\text{coat}}) $ 沉积在另一块基底板材 $ S_{\text{sub}}=\text{Slab}(f_{\text{sub}},V_{\text{sub}}) $ 或复合材料之上来生成一种复合材料,从概念上讲是将 $ S_{\text{coat}} $ 的介电介质基底与 $ S_{\text{sub}} $ 的表面键合,使得 $ V_{\text{coat}} $ 成为 $ S_{\text{sub}} $ 顶部界面的相邻介质。
将两个独立的板材 $ S_{\text{sub}} $ 和 $ S_{\text{coat}} $ 通过物理方式结合并键合在一起,产生了一种在微观尺度上"垂直"异质的新型复合材质 $ L $,表示为:
图解上,我们将层叠操作表示为将两块板材垂直相邻放置,可以想象这两块物理材质层在它们的顶部和底部界面处被键合。
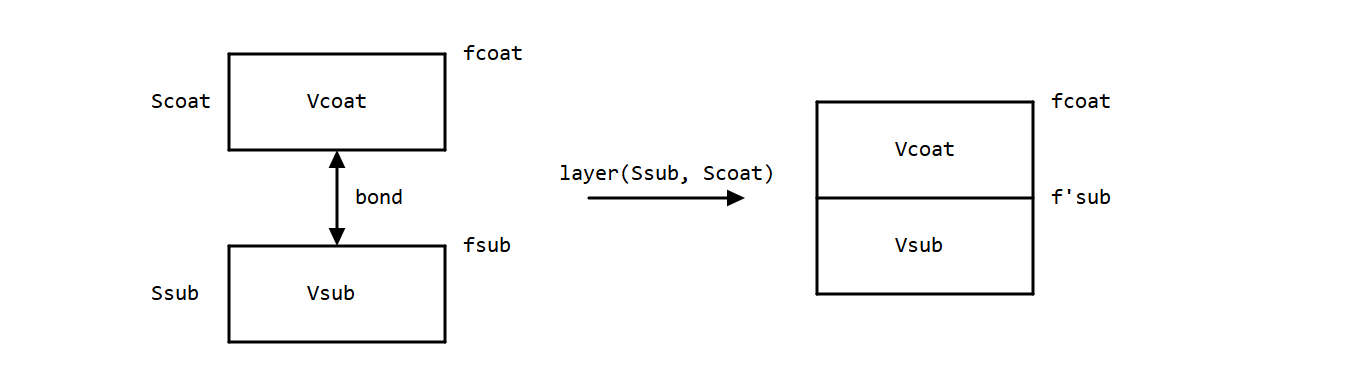
可以理解的是,由涂层和基层结合形成的新内部界面的 BSDF $ f_{\text{sub}}^{\prime} $ 不一定与 $ S_{\text{sub}} $ 的原始 BSDF $ f_{\text{sub}} $ 相同,但可以通过考虑键合的物理和几何特性从中推导出来。从物理角度来看,该 BSDF 应与相邻介质 $ V_{\text{coat}} $ 和 $ V_{\text{sub}} $ 保持一致,并且假设键合不会显著改变基层界面的几何形状(即涂层顺应基板的几何形状)。那么,考虑到层叠中被键合的组成层的已知 BSDF 和介质,以及用于描述最终界面的一整套参数,内部界面的 BSDF 应如何实现是相当明确的。例如,将两个介电板材结合在一起,会根据介电介质折射率(IOR)的比率在界面处产生众所周知的菲涅尔效应。
请注意,从技术上讲,$ \textbf{layer} $ 操作符是结合性的,即:
因为它们描述了等效的物理配置。
将物理层结构映射到渲染器中可用的形式取决于特定用例所需的近似水平。通常,光传输属性将由代表模型生成的各个波瓣的 BSDF 表示,我们可以粗略地将其与每个板材的顶部界面的 BSDF 识别起来。然后,层叠操作的结果 BSDF 可以通过各种组合各个界面 BSDF 的方案来近似。
例如,给定上述一般情况,即介电涂层叠在基板上,表示为 $ \textbf{layer}(S_{\text{sub}},S_{\text{coat}}) $,这产生了一个具有可推导 BSDF $ f_{\text{sub}}^{\prime} $ 的内部界面和一个具有 BSDF $ f_{\text{coat}} $ 的介电顶部界面,中间夹着介电涂层介质 $ V_{\text{coat}} $。
这种分层配置最简单的表示方式相当于对界面BSDF $ f_{\text{sub}} $ 和 $ f_{\text{coat}} $ 进行某种线性组合。一种常见的方法是所谓的反照率缩放近似法,其中该分层配置的总BSDF由 $ f_{\text{coat}} $ 和 $ f_{\text{sub}} $ 相加给出,其中基底波瓣的加权因子等于(1减去涂层的定向反射率),这样设计是为了确保最终的BSDF是能量守恒的:
其中定向反照率积分 \(E_{\text{coat}}(\omega_{o})\) 可以预先计算并制成表格,或者通过对BSDF进行蒙特卡洛采样来实时计算。这种形式确保了如果涂层和基底BSDF的方向反照率是能量守恒的(即 \(E_{\text{coat}}(\omega_{o})\leq 1\), \(E_{\text{sub}}(\omega_{o})\leq 1\)),那么组合后的BSDF也是能量守恒的,因为:
它还确保如果基底BSDF完美地保持能量,即 \(E_{\text{sub}}(\omega_{o})=1\),那么分层BSDF也能做到这一点,从而确保能通过“白炉”测试。Autodesk标准表面模型 [Georgiev2019] 在其分层中使用了这种公式。
但请注意,这种反照率缩放近似法并未正确考虑光在界面之间来回多次反弹的效应,或涂层体积介质 $ V_{\text{coat}} $ 中的吸收和散射。通常,最终的BSDF波瓣形状将不是界面BSDF的简单线性组合。在某种程度上,可以通过各种近似将这些效应重新纳入反照率缩放模型中。例如,穿过涂层的体积透射率在入射和出射方向上的效应可以近似建模为:
其中 \(T_{\text{coat}}(\omega_{i},\omega_{o})\) 解释了沿着输入和输出射线的涂层总体积吸收。类似地,如果涂层是粗糙的,这也会有效地使基底BSDF波瓣变粗糙,这可以通过各种启发式方法近似地加以考虑。
完全的规范符合性被定义为重现所有物理层间光传输效应,尽管这通常不切实际。在实践中,每个实现必须决定对层内光传输使用何种程度的近似,根据其特定用例在精度和效率之间进行权衡。
2.3 混合
许多真实世界的物体由多种不同材料以斑块形式排列组成,例如生锈物体上的金属和氧化物区域。通过在其表面纹理化每种材料类型来建模此类物体的外观十分方便。虽然现实中材料过渡通常是突变的,但连续混合材料的能力对于艺术目的和抗锯齿都很有用。
混合操作(mix operation) 在微观尺度上模拟了两种材料之间的线性混合。其物理图景是:微观表面由每种材料按混合权重比例随机分布的斑块组成,从而在"水平"方向上呈现异质性。两层 $ S_{0} $ 和 $ S_{1} $ 以权重 $ w_{1} $ 进行混合操作,生成一种新的"水平"异质复合材质 M,表示为:
其中当 $ w_{1}\to 0 $ 时 $ M\to S_{0} $,当 $ w_{1}\to 1 $ 时 $ M\to S_{1} $。图解上,我们将混合表示为将两层水平相邻放置,意图是想象物理层位于同一表面水平相邻,但以微观斑块形式随机分布,相对面积与给定的混合权重成比例。

(图示说明:两个标有v0和v1的矩形,分别代表S0和S1,其宽度占比由1-w1和w1表示,矩形上方标有f0和f1)
混合操作也用于描述特定点处材质中存在特定层结构的概率。例如,涂层 $ S_{\text{coat}} $ 可能覆盖基底层 $ S_{\text{sub}} $,但可能是间歇性的,仅应用于基底的某个分数 $ w_{\text{coat}} $(涂层存在或覆盖权重)。这将指定为:
为方便起见,这也可以更简洁地写为一个加权层操作符,用涂层覆盖基底的给定分数:

(图示说明:一个大矩形被分割为两部分:左侧为Ssub,占1-wcoat宽度;右侧为上下排列的Scoat和Ssub,占wcoat宽度)
在最底层被混合的体材质明显不一致的情况下(例如混合介电体和金属体),混合操作的这种物理图景在某些情况下会变得不太现实,但在这种情况下,理解上实现应该尽力使其物理意义合理。例如,金属体实际上可以被认为是在单一一致介电体表面的金属薄片。
在渲染器中实现混合操作取决于材质模型的近似方式。通常,模型将被简化为每个被混合板材的有效BSDF,在这种情况下,混合可以简单地实现为这些BSDF的线性混合,即如果板材 \(S_{0}\)、\(S_{1}\) 分别具有BSDF \(f_{0}\)、\(f_{1}\),那么 \(\text{mix}(S_{0},S_{1},w_{1})\) 的BSDF可以映射为:
在加权层操作的情况下,如果基底的BSDF是 $ f_{\text{sub}} $,那么 $ \text{layer}(S_{\text{sub}},S_{\text{coat}},w_{\text{coat}}) $ 映射为:
其中 $ f_{\text{layer}} $ 是对应于 $ \textbf{layer}(S_{\text{sub}}, S_{\text{coat}}) $ 的BSDF。如果我们使用分层章节中描述的非互易反照率缩放方法(公式9),那么 $ f_{\text{layer}} $ 可以表示为:
其中 $ f_{\text{coat}} $ 是涂层的BSDF,$ T_{\text{coat}} $ 是其透射率。因此将这些组合起来 $ {}^{3} $:
例如,这是Autodesk标准表面[Georgiev2019]涂层中使用的公式。
通过这种方式,抽象的混合和分层操作可以映射到更便于计算的近似表示,即BSDF波瓣的加权和(更多细节请参见"简化为波瓣混合"章节)。
2.4 自发光
每层还有一个发射分布函数(EDF),尽管默认情况下对应完全不发射。发射属性以光度单位表示,因为参考值广泛可用。因此EDF是一个定向亮度函数 $ L_{e} $。可以想象亮度从层内部均匀发射(通过某种未指定的物理过程)。转换为辐射度单位是渲染器的责任。对于RGB渲染器,[Lagarde2014]中提出了一个简单的近似方法。在本模型中,我们通常假设发射在所有方向上均匀分布到半球中。整个结构的发射随后(原则上)由从发射层通过其邻居传播到周围空间的发射光物理确定。
2.5 元数据
本规范旨在促进可能使用不同渲染引擎和渲染管线的设施之间的资产交换。为此,它试图减少最终外观的歧义,以便如果实现合理符合规范,资产可以预期在视觉上大致相同地渲染。
然而,我们描述的物理模型的参数并未指定获得良好视觉匹配所需的所有假设。因此,为了资产交换的目的,我们建议将参数与提供以下缺失信息的某些元数据打包:
● 实现的规范版本
● 所有颜色参数的假定色彩空间。如果未指定,遵循MaterialX[Smythe2016],默认情况下该色彩空间假定为ACEScg
● 从世界空间长度单位到米的浮点转换因子
● 任何提供的纹理文件与它们指定的参数之间的关联,根据几何体的局部UV坐标生成空间变化的参数
● 驱动模型参数的着色器网络
● 如果存在,将输入的 \(geometry\_normal、geometry\_coat\_normal、geometry\_tangent 和 geometry\_coattangent\)贴图转换为每个点局部表面最终着色法线的假定约定
由于在实践中OpenPBR将集成在MaterialX和USD等数据交换框架中,此元数据的具体形式和内容不在本规范范围内。
