ECC 学习笔记

0. 前置知识

给定集合 \(S\) 和运算 \(\circ\)，若 \(\circ\) 对 \(S\) 封闭，且有单位元（\(a \circ e = a\)）、逆元（\(a \circ a^{-1} = e\)）、结合律、交换律，则称 \(S\) 对 \(\circ\) 构成 Abelian 群。

一个大人遇到了一个小孩。

大人：你知道 \(7 + 5\) 等于多少吗？

小孩：不知道。

大人：那你知道 \(5 + 7\) 等于多少吗？

小孩：不知道。

大人：那你知道什么？

小孩：我知道 \(7 + 5 = 5 + 7\)，因为 \(\Z\) 对 \(+\) 构成 Abelian 群。

1. 椭圆曲线（EC）

1.1 定义

我们定义满足 Weierstrass 方程（\(y^2 = x^3 + ax + b\)）的点集为椭圆曲线。下面是 \(a = -2, b = 5\) 时的图像。

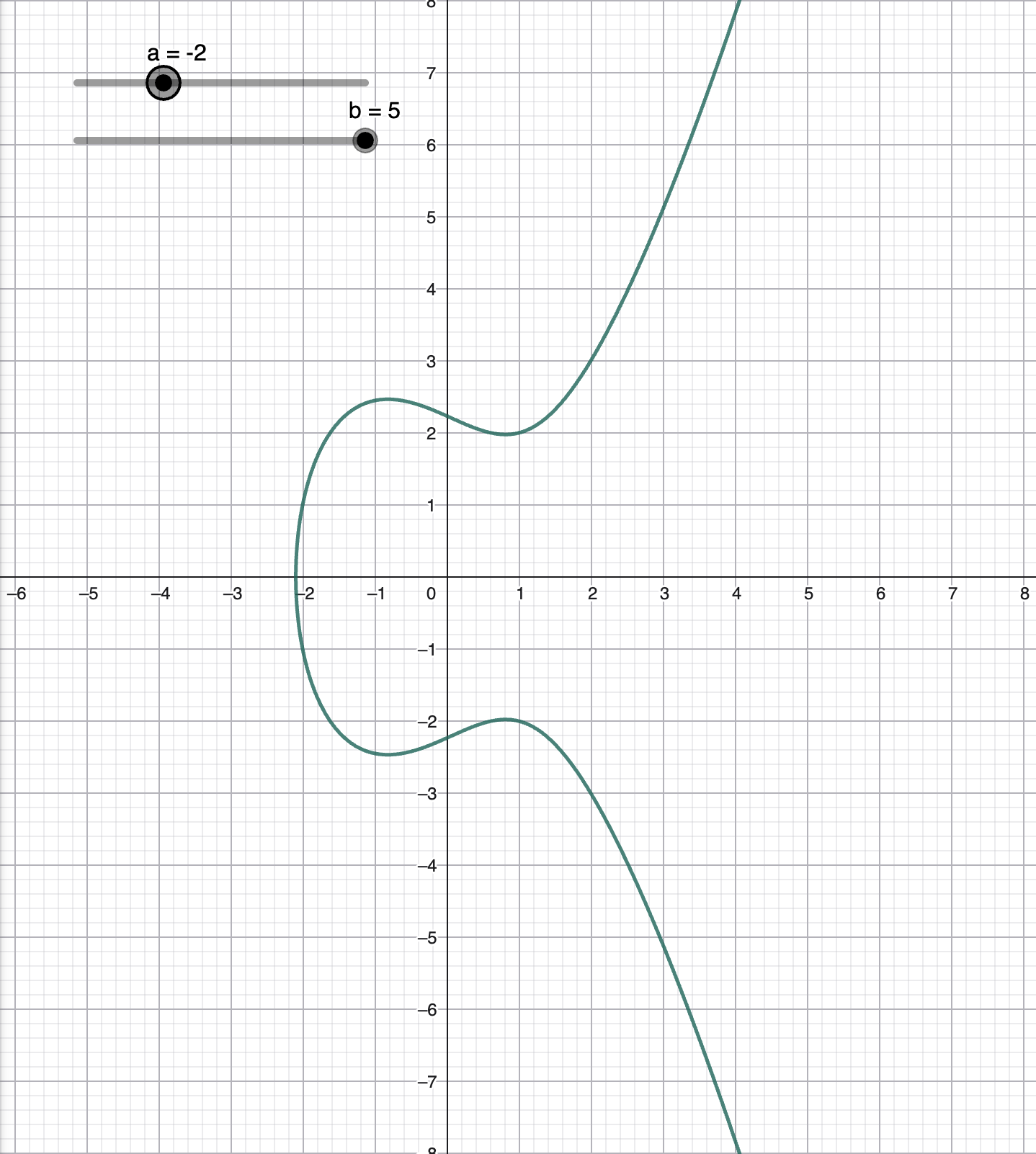
容易发现图像关于 \(x\) 轴对称。

计算机计算浮点数的效率不高，所以计算时一般使用同余形式：

\[y^2 \equiv x^3 + ax + b \pmod p \]

其中 \(p\) 是一个大质数。

一般会额外定义一个无穷远点 \(\mathcal{O}\)，规定 \(\mathcal{O}\) 也属于椭圆曲线。

注：此处的无穷远点需要从射影几何的角度去理解，但笔者不会射影几何。早知道之前就学一下了。

1.2 点的加法

现有椭圆曲线 \(E : y^2 = x^3 + ax + b\)，对于两点 \(P, Q \in E\) 定义：

• \(P \neq Q\) 时：设 \(PQ\) 交 \(E\) 于 \(R\)，\(P + Q\) 为 \(R\) 关于 \(x\) 轴的对称点。
• \(P = Q\) 时：作 \(E\) 在 \(P\) 上的切线 \(l\)，设 \(l\) 交 \(E\) 于 \(R\)，\(P + Q\) 为 \(R\) 关于 \(x\) 轴的对称点。
• \(P\) 与 \(Q\) 关于 \(x\) 轴对称时：\(P + Q = \mathcal{O}\)，\(Q = -P\)。
• \(P + \mathcal{O} = \mathcal{O} + P = P\)。

容易发现，\(P + Q \in E\)，且 \(+\) 满足交换律。\((E, +)\) 构成 Abelian 群：

• 单位元：\(\mathcal{O}\)。
• 逆元：\(P\) 的逆元为 \(P\) 关于 \(x\) 轴的对称点。
• 结合律：证明需要射影几何知识，或暴算。
• 交换律：显然满足。

我们来进行一些计算。设 \(P = (x_1, y_1), Q = (x_2, y_2), R = P + Q = (x_3, y_3)\)，我们考虑求出 \(x_3, y_3\)。下设 \(P \neq \mathcal{O}, Q \neq \mathcal{O}, R \neq \mathcal{O}\)。

经过计算可知，设：

\[\lambda = \begin{cases}\dfrac{y_2 - y_1}{x_2 - x_1}, &P \neq Q \\\dfrac{3x_1^2 + a}{2y_1} &P = Q \end{cases} \]

则：

\[\begin{aligned}x_3 &= \lambda^2 - x_1 - x_2 \\y_3 &= \lambda (x_1 - x_3) - y_1 \end{aligned} \]

如果你考虑了可行性，会发现 \(P = Q\) 时切线可能不唯一，我们要避免这种情况的发生。那么考虑求出这种情况的充要条件。

从特殊到一般。发现切线不唯一有至少两种情况：尖点或相交。

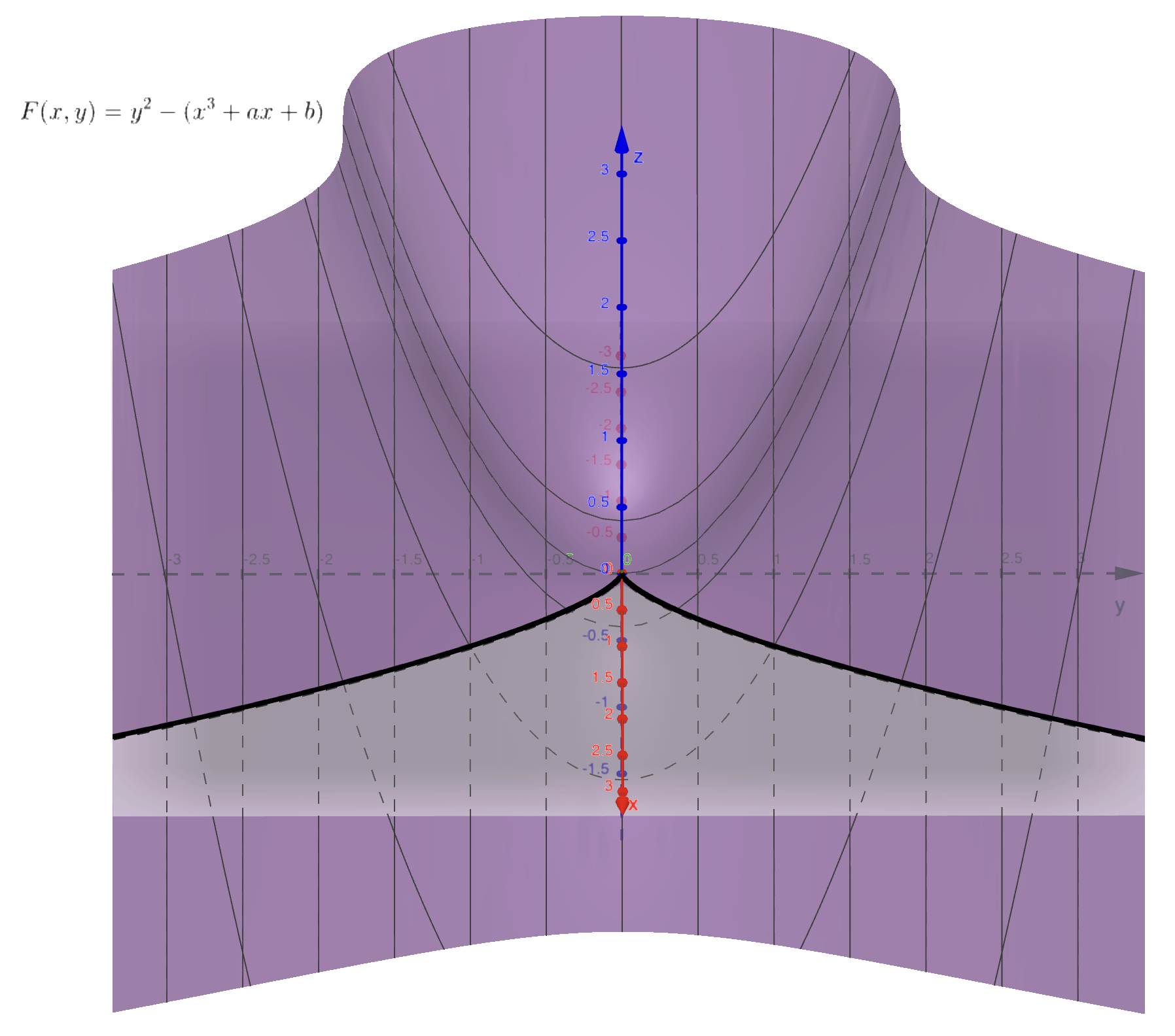
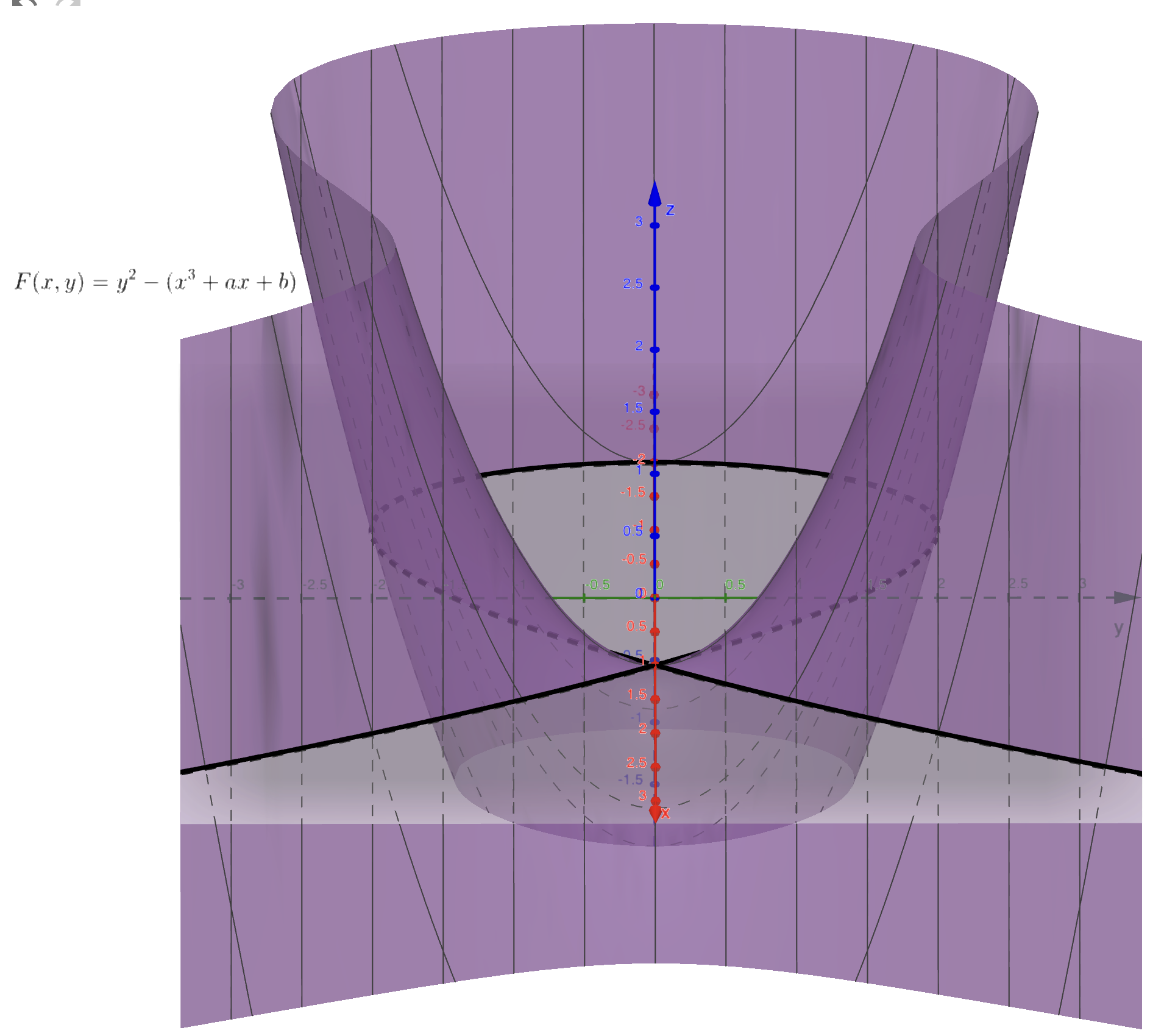
图中 \(F\) 与 \(z = 0\) 的交线为椭圆曲线。猜猜为什么要这样画图。

以尖点的情况举例，我们考虑 \(\dfrac{\partial F}{\partial x}\) 和 \(\dfrac{\partial F}{\partial y}\)。

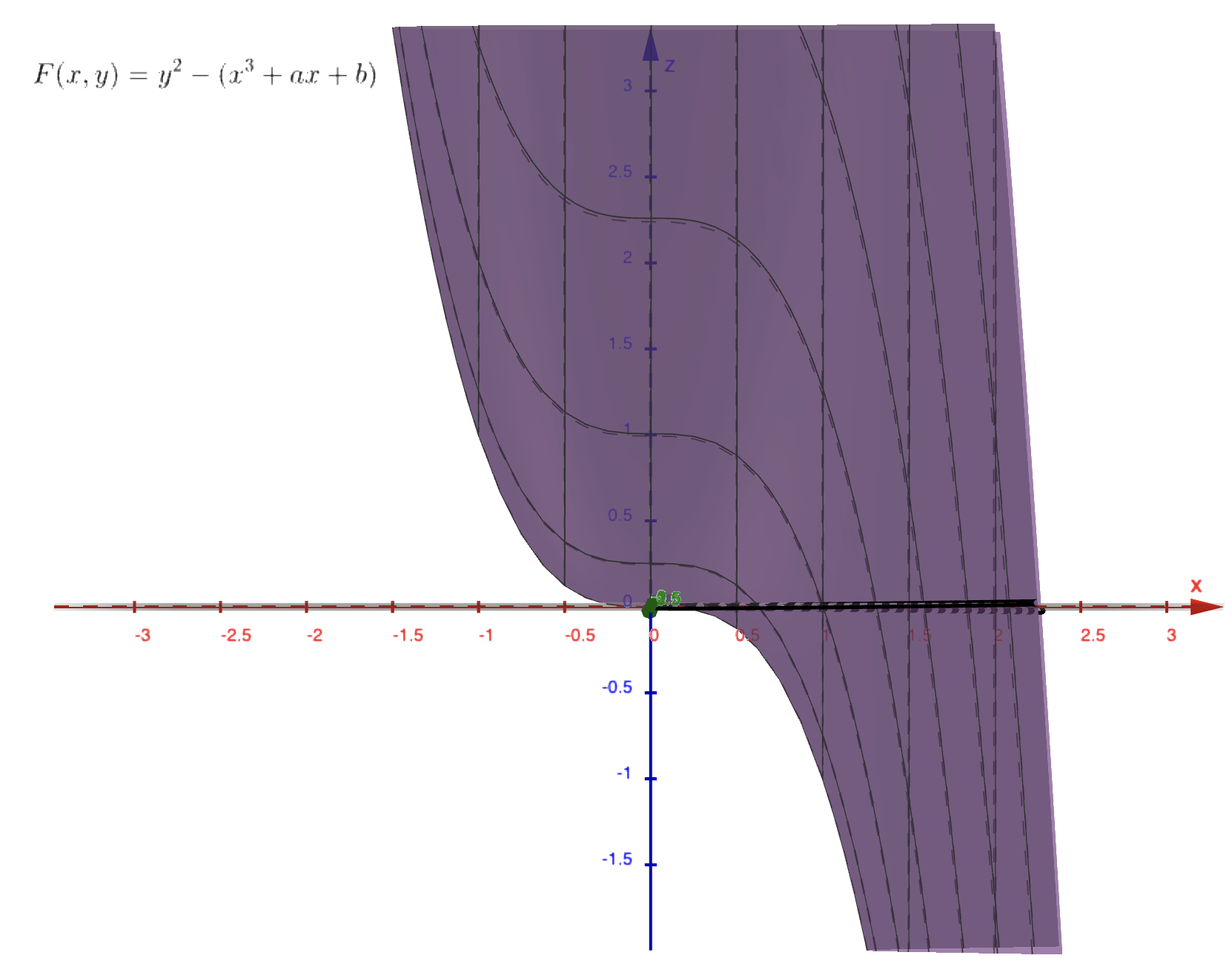
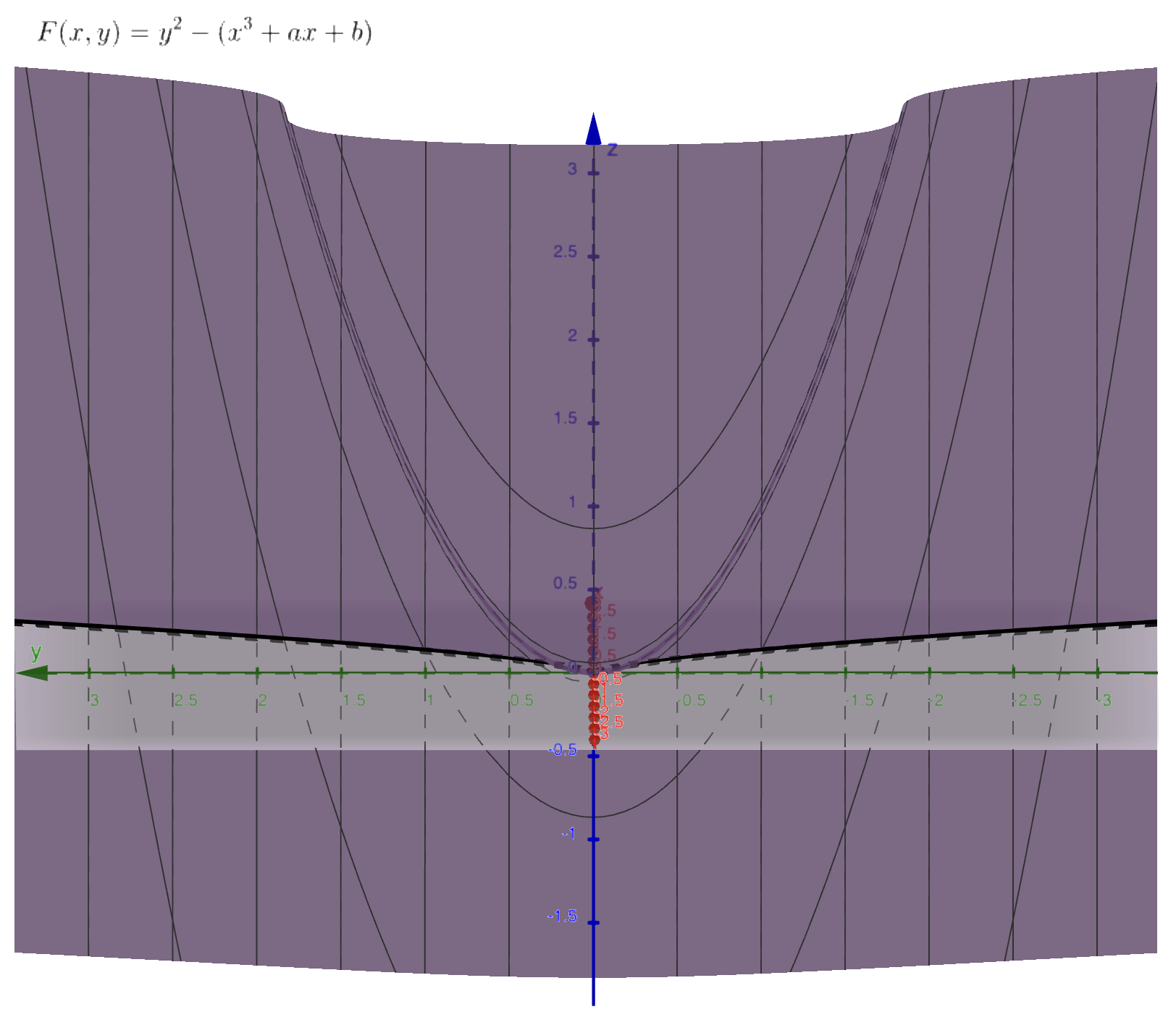
猜猜 \(a, b\) 的值。

观察到尖点满足 \(F = \dfrac{\partial F}{\partial x} = \dfrac{\partial F}{\partial y} = 0\)。可以证明，这是充要条件。但我不会证。

算出来 \(\dfrac{\partial F}{\partial x}\) 和 \(\dfrac{\partial F}{\partial y}\)：

\[\begin{aligned}\dfrac{\partial F}{\partial x} &= 3x^2 + a \\\dfrac{\partial F}{\partial y} &= 2y \end{aligned} \]

则 \(x = \dfrac{\sqrt{-3a}}{3}, y = 0\)。代入 \(E\)：

\[0 = \left( \dfrac{\sqrt{-3a}}{3} \right)^3 + a \cdot \dfrac{\sqrt{-3a}}{3} + b = \dfrac{2a}{9} \sqrt{-3a} + b \]

两边平方得：

\[b^2 = -\dfrac{4a^3}{27} \]

即：

\[\begin{align}4a^3 + 27b^2 = 0 \end{align} \]

所以这种情况发生的充要条件就是 \((1)\) 式。

1.3 点的数乘

现有椭圆曲线 \(E : y^2 = x^3 + ax + b\) 与点 \(P\)，定义 \(kP = \underbrace{P + P + \cdots + P}_k\)，其中 \(k \in \N\)。

如何快速计算 \(kP\)？考虑快速幂，因为：

\[kP = \begin{cases}\left \lfloor \dfrac{k}{2} \right \rfloor P + \left \lfloor \dfrac{k}{2} \right \rfloor P, &2 \mid k \\\left \lfloor \dfrac{k}{2} \right \rfloor P + \left \lfloor \dfrac{k}{2} \right \rfloor P + P &2 \nmid k \end{cases} \]

所以可以 \(O(\log k)\) 递推计算。

发现当 \(kP = \mathcal{O}\) 时比较特殊。对于点 \(P\)，定义 \(P\) 的阶为最小的正整数 \(k\) 满足 \(kP = \mathcal{O}\)。

2. 椭圆曲线离散对数问题（ECDLP）

题目：给定点 \(P, Q\)，考虑求解 \(k\) 满足 \(Q = kP\)。

因为每次加法 \(x\) 坐标的指数都会乘 \(2\)，所以这实际上是在求解离散对数问题。

不幸的是，离散对数问题仍不存在多项式时间的算法。常用的算法为 BSGS 算法，但时间复杂度为 \(O \left( \sqrt{m} \right)\)，其中 \(m\) 为模数。一般情况下 \(m \ge 2^{128}\)，所以 BSGS 算法运行时间是不现实的。基于这一点，人们设计出了许多加密算法，如 RSA。

3. Diffie-Hellman 算法

用途

一般被用于密钥协商。

流程

0. Alice 和 Bob 使用同一个椭圆曲线 \(E\) 和基点 \(G\)（阶为大质数 \(q\)）。
1. Alice 随机生成私钥 \(d_A\)，计算公钥 \(Q_A = d_A G\)。Bob 随机生成私钥 \(d_B\)，计算公钥 \(Q_B = d_B G\)。
2. Alice 向 Bob 发送 \(Q_A\)，Bob 向 Alice 发送 \(Q_B\)。
3. Alice 计算出共同密钥 \(S = d_A Q_B\)，Bob 计算出共同密钥 \(S = d_B Q_A\)。

注意到 \(d_A Q_B = d_B Q_A = d_A d_B G\)，所以两人获得了同一个密钥。

4. ElGamal 算法

用途

用于加密 / 解密消息。

流程

0. Alice 和 Bob 使用同一个椭圆曲线 \(E\) 和基点 \(G\)（阶为大质数 \(q\)）。
1. Bob 随机生成私钥 \(d \in (1, q)\)，并计算公钥 \(Q = dG\)。

加密

假设 Alice 要发送消息 \(M\) 给 Bob。

2. 把 \(M\) 变换到 \(E\) 上，设变换后为 \(M'\)。
3. 选择随机整数 \(k \in (1, q)\)。
4. 计算 \((C_1, C_2) = (kG, M' + kQ)\)。
5. 发送 \((C_1, C_2)\) 给 Bob。

解密

2. 计算 \(M' = C_2 - kQ = C_2 - kdG = C_2 - dC_1\)。
3. 通过 \(M'\) 变换回 \(M\)。

攻击方法

发现对于不同的 \(k\)，计算 \(kQ\)（或其他数乘）的时间是不同的，所以理论上可以测量计算 \(kQ\) 的时间（或其他信息）来获知 \(k\)。CTF 对于上述攻击方法出了一道题，当然我是不会做的。