数据结构篇开篇:了解基本概念会算复杂度,也会选结构!
一、基本概念
数据结构是一门研究如何有效组织数据,并提高数据处理效率的学科。通过研究各种数据内部的逻辑关系,使用某种特定的存储形式,并在此基础上对数据实施各种操作,这些工作被称为广义上的算法。
逻辑结构
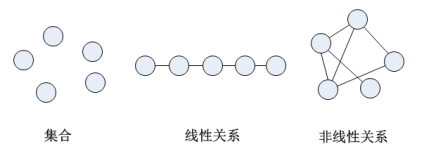
线性关系:
各个元素之间是一种一对一的关系,比如图书馆中的书架的书,除了首尾两本书之外,其余的任意一本书的编号假设是N,都有且仅有一个直接前驱节点(上一个节点)N-1,有且仅有一个直接后继节点(下一个节点)N+1。这种关系就是典型的线性逻辑。
非线性关系:
与上述线性关系的表述不同,如果各个元素之间不是严格一对一的关系,则被称为非线性关系,比如家族中的各个成员、不同城市间的交通道路等,对于它们中间的某个元素,都可能有不止一个元素与之关联。
二、存储形式
数据的存储方式。比如顺序存储、链式存储等。
逻辑结构与存储形式并无必然联系。
| 存储方式 | 特征 | 时间访问 | 空间额外 | 嵌入式场景 |
|---|---|---|---|---|
| 顺序存储 | 连续内存 | O(1) 随机 | 无 | 静态数组、DMA 缓冲区 |
| 链式存储 | 指针离散 | O(n) 顺序 | 指针域 | 可变长度消息队列 |
| 索引存储 | 索引表 + 数据 | O(log n) | 索引开销 | Flash 文件系统 |
| 散列存储 | 哈希函数 | O(1) 平均 | 哈希桶 | 快速查找表 |
存储密度 = 数据域大小 / 结点总大小
链式结构密度 < 顺序结构,MCU 内存紧张时优先顺序

三、算法分析
算法分析是指算法在正确的情况下,对其优劣的分析。一个好的算法通常是指:
- 时间少
- 空间少
- 易读、易移植、易调试
① 时间复杂度
一般而言,时间复杂度并不考察一段代码运行所需要的绝对时间,因为不同的计算机的硬件参数不同,考察绝对时间没有意义。时间复杂度一般指的是代码的语句执行总次数,称为语句频度。
示例:
void counting(int n){for(int i=0; i<n; i++){printf("本行语句将会出现n次\n");for(int j=0; j<n; j++){printf("本行语句将会出现n*n次\n");}}
}
语句频度:T(n)=n²+n → 大O表示法:O(n²)
大O速查表(常用)
| 复杂度 | 名称 | 举例 | 嵌入式提示 |
|---|---|---|---|
| O(1) | 常数 | 数组随机访问 | 最优先 |
| O(log n) | 对数 | 二分查找 | 推荐 |
| O(n) | 线性 | 遍历数组 | 可接受 |
| O(n log n) | 线性对数 | 快速排序 | 慎用递归 |
| O(n²) | 平方 | 冒泡排序 | 小数据可用 |
| O(2ⁿ) | 指数 | 暴力穷举 | 禁止在 MCU |
② 空间复杂度(原文保留 + 拓展)
空间复杂度的概念更简单一点,就是一段程序运行时所需的内存字节量。
拓展:
| 内存区域 | 用途 | 建议 |
|---|---|---|
| 栈 | 局部变量、函数调用 | < 8 KB,避免大数组 |
| 堆 | 动态分配 | 能不 malloc 就不 malloc |
| 静态区 | 全局变量、static | 编译期确定,可控 |
| ROM/Flash | 常量、代码 | 只读,存查找表 |
③ 时空复杂度互换
一段程序的性能指标,既要运行快速,又要节省内存,而通常这两者又是相互制约的,很难兼得。因此在实际解决问题时,会根据需要侧重一方,牺牲另一方。
