当前位置： 首页 > news >正文

完整教程：数据结构 栈和队列、树

news 2025/9/21 15:59:16

完整教程：数据结构 栈和队列、树

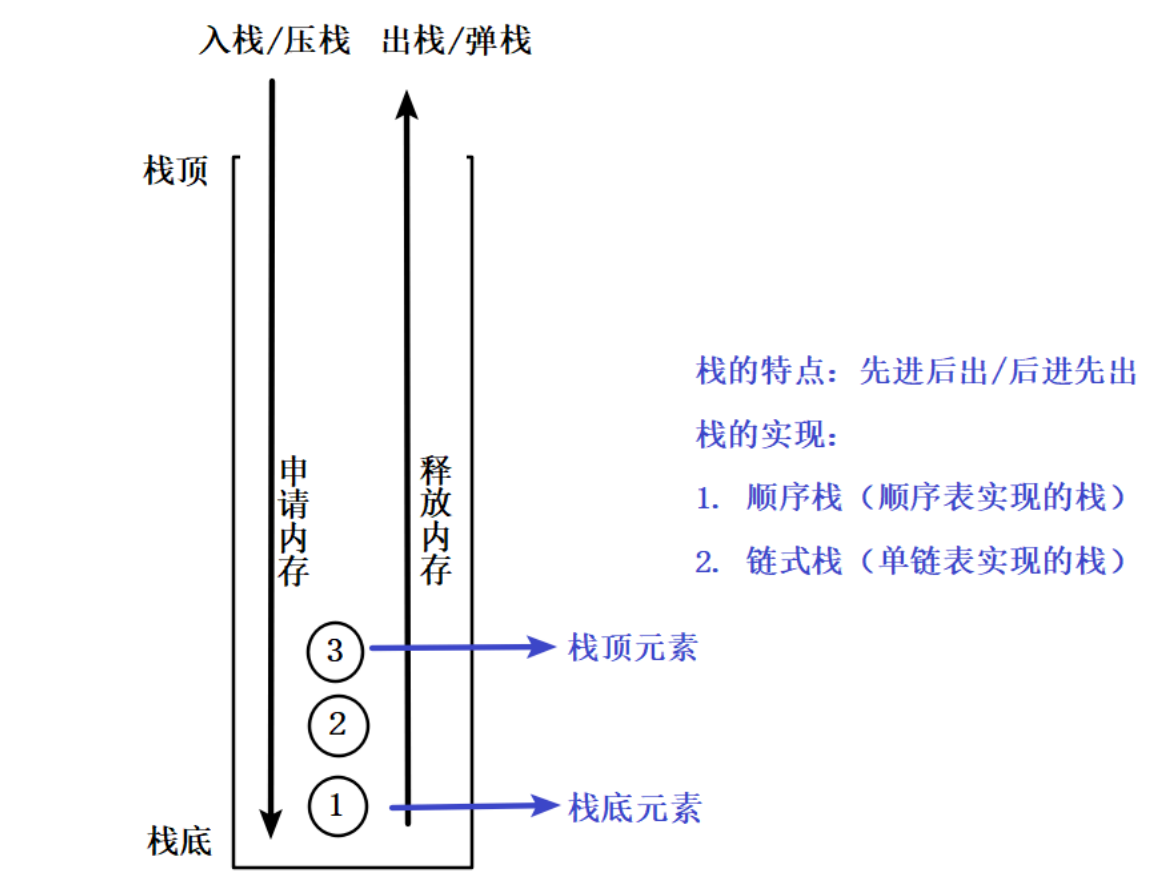
栈

栈是一种逻辑结构，是特殊的线性表。特殊在：

只能在固定的一端操作（称为栈顶）

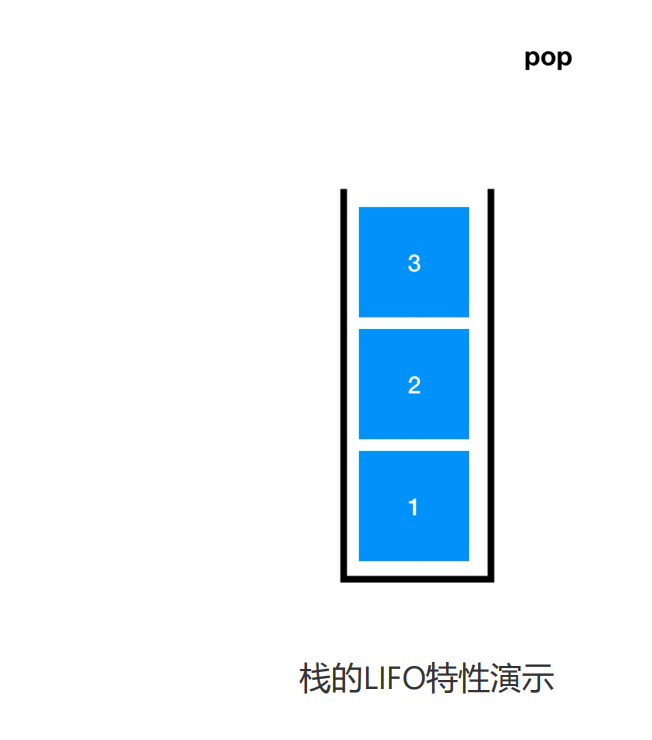
只要满足上述条件，这种特殊的线性表就会呈现"先进后出 / 后进先出"（LIFO）的逻辑特

性。栈在生活中随处可见，比如：

堆叠的盘子：最后放上去的盘子最先被取下来

函数调用：最后调用的函数最先返回

撤销操作：最近的修改最先被撤销

术语定义

由于只能在固定端操作，栈有以下特定术语：

栈顶(Top)：允许插入和删除的一端

栈底(Bottom)：固定不变的另一端

入栈/压栈(Push)：将元素插入栈顶

出栈/弹栈(Pop)：删除栈顶元素

取栈顶(Top/Peek)：获取但不删除栈顶元素

循环栈（数组实现）

使用连续内存存储元素，需要管理结构体记录状态：

squence_stack.h

#ifndef  SQUENCE_STACK_H
#define  SQUENCE_STACK_H
#include
#include
#include
//定义数据类型的别名
typedef int DATA;
//循环栈的定义
typedef struct {
DATA* data; //数据指针域
int size; //栈的容量
int top; //栈顶的下标
}Seqstack;
//栈的初始化
/*
s 是待操作的栈
num 是栈的容量
成功返回0，失败返回-1
*/
int Seq_init(Seqstack* s, int num);
/*
入栈或者压栈
s 是待操作的栈
data 是栈的数据(栈元素)
成功返回0，失败返回-1
*/
int Seq_push(Seqstack* s, DATA data);
/*
出栈
s 是待操作的栈
data 是栈的数据(栈元素)
成功返回0，失败返回-1
*/
int Seq_pop(Seqstack* s, DATA*data);
/*
判断栈是否满了
已满返回1，未满返回0
*/
int Seq_isfull(Seqstack* s);
/*
判断栈是否为空
已满返回1，未满返回0
*/
int Seq_isempty(Seqstack* s);
//销毁栈
void Seq_destory(Seqstack* s);
#endif

squence_stack.c

#include "squence_stack.h"
int Seq_init(Seqstack* s, int num) {
//做非空校验
if (!s)return -1;
//分配动态空间分配num个单位的空间相当于数组
s->data = (DATA*)calloc(num, sizeof(DATA));
if (!s->data)return -1;
//循序栈的初始化
s->size = num;
s->top = -1;//默认为-1
return 0;
}
int Seq_isfull(Seqstack* s) {
return s->top + 1 == s->size;//栈已满
}
int Seq_isempty(Seqstack* s) {
return s->top == -1;
}
int Seq_push(Seqstack* s, DATA data) {
if (Seq_isfull(s))
{
return -1;
}
s->top++;
s->data[s->top] = data;//存放元素 修改data里面的值
return 0;
}
int Seq_pop(Seqstack* s, DATA* data) {
if (Seq_isempty(s))
{
return -1;
}
*data = s->data[s->top]; 出栈的时候，出一次打印一次top一直在变化
s->top--;
return 0;
}
void Seq_destory(Seqstack* s) {
if (!s)
{
return;
}
if (s->data != NULL)
{
free(s->data);
s->data = NULL;
}
s->top = -1;
s->size = 0;
}

main.c

#include "squence_stack.h"
int main() {
Seqstack s;
DATA temp;
// 初始化容量为10的栈
if (Seq_init(&s, 10) != 0)
{
perror("栈初始化失败！");
return -1;
}
// 入栈测试
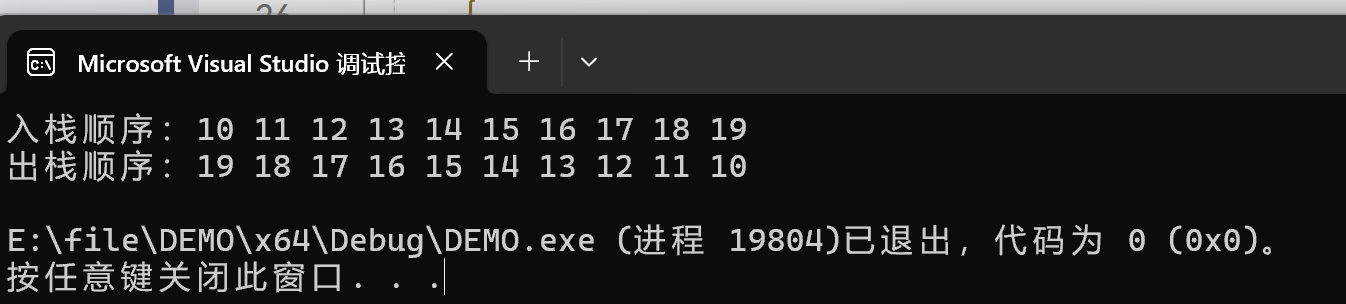
printf("入栈顺序：");
for (int i = 0; i < 10; i++)
{
Seq_push(&s, i + 10); // 入栈 10 ~ 19
printf("%d ", i + 10);
}
// 出栈测试
printf("\n出栈顺序：");
while (!Seq_isempty(&s))
{
Seq_pop(&s, &temp); 出栈是一个一个出
printf("%d ", temp);
}
printf("\n");
// 销毁栈
Seq_destory(&s);
return 0;
}

链式栈（链表实现）

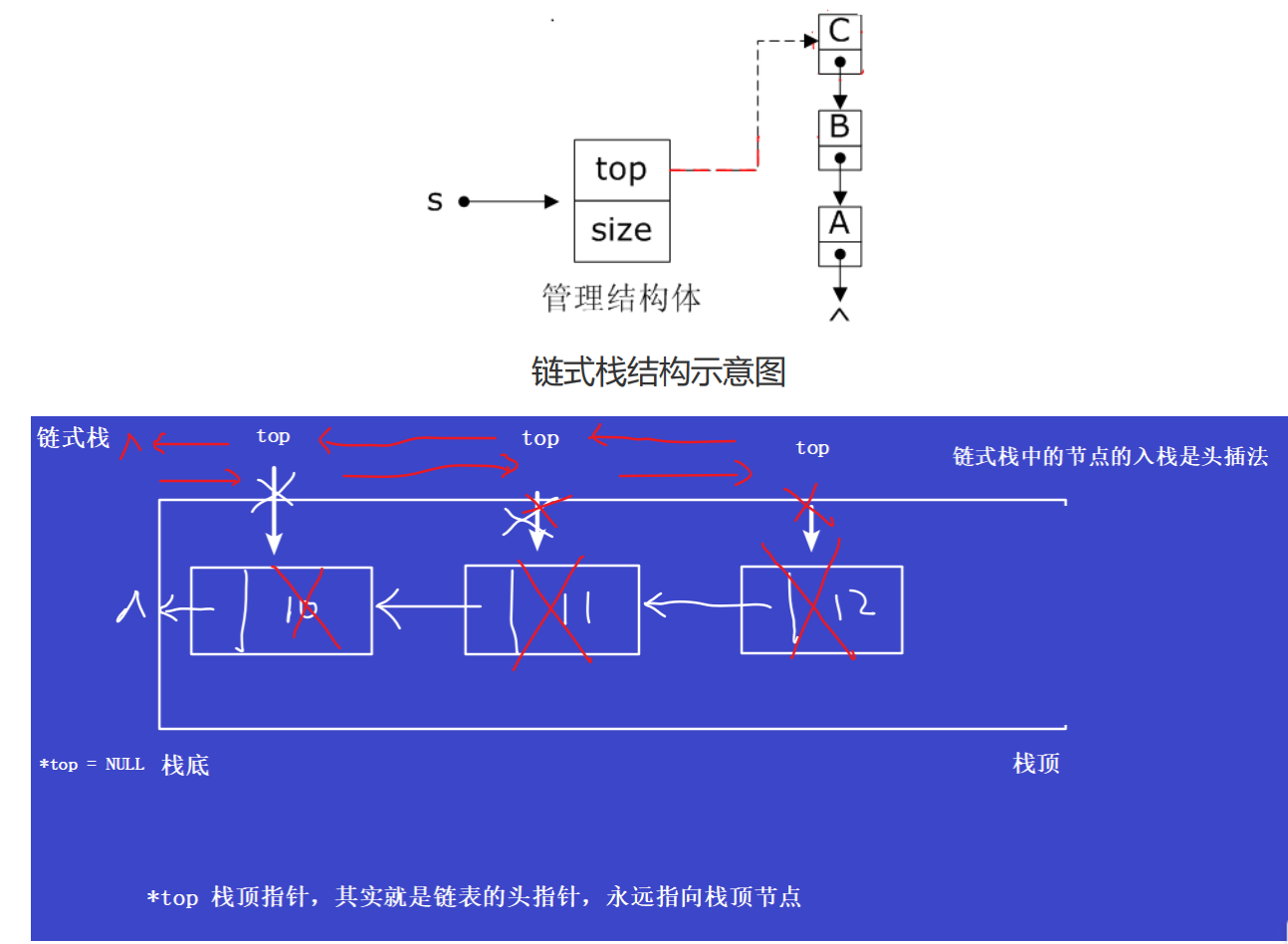
link_stack.h

#ifndef LINK_STACK_H
#define LINK_STACK_H
#include
#include
#include
//定义数据
typedef int DATA;
//定义链式节点
typedef struct node{
DATA data;
struct node* next;
}NODE;
//定义链式栈
typedef struct{
NODE* top;//栈顶指针
int size;//栈中元素的个数
int capacity;//栈容量
}link_stack;
//初始化栈 s是待操作的栈，num是栈中元素的个数
int stack_init(link_stack* s, int num);
//入栈 s是待操作的栈，data是入栈的元素
int stack_push(link_stack* s, DATA data);
//出栈 s是待操作的栈，*data是出栈的元素
int stack_pop(link_stack* s, DATA *data);
//判断栈是否已满
int stack_isfull(link_stack* s);
//判断栈是否为空
int stack_isemty(link_stack* s);
//销毁栈
int stack_destroy(link_stack* s);
#endif

link_stack.c

#include "link_stack.h"
int stack_init(link_stack* s, int num) {
if (!s) return -1;
s->top = NULL;//栈的头指针置为空
s->size = 0;//栈的个数初始化为0
s->capacity = num;//入栈的个数是当前的容量
return 1;
}
int stack_push(link_stack* s, DATA data) {
if (!s)return -1;
if (stack_isfull(s))
return -1;
//创建节点
NODE* newNode = (NODE*)malloc(sizeof(NODE));
if (!newNode)return -1;
newNode->data = data;
newNode->next = s->top;//第一个头指针初始化为NULL了，当前节点
s->top = newNode;    //当前的头指针指向新节点
s->size++;
}
int stack_isfull(link_stack* s) {
if (!s)return 0;
return s->size >= s->capacity;
}
int stack_isemty(link_stack* s) {
if (!s)return 0;
return s->size == 0;
}
int stack_pop(link_stack* s, DATA* data) {
if (!s) return -1;
//用另一个指针接收原指针目的是为了，不操作原指针，指针越界超出，也不影响原指针
if (stack_isemty(s))return -1;
NODE* temp = s->top;//头节点元素地址
*data = temp->data;
s->top = temp->next;//头节点元素是下一个节点
s->size --;//更新出栈的元素
free(temp);
}
int stack_destroy(link_stack* s)
{
DATA temp;
// 循环弹出所有元素
while (!stack_isemty(s))
{
stack_pop(s, &temp);
}
return 0;
}
#include "link_stack.h"
int main() {
link_stack s;
DATA temp;
// 1. 初始化容量为10的链式栈
stack_init(&s, 10);
// 2. 入栈测试
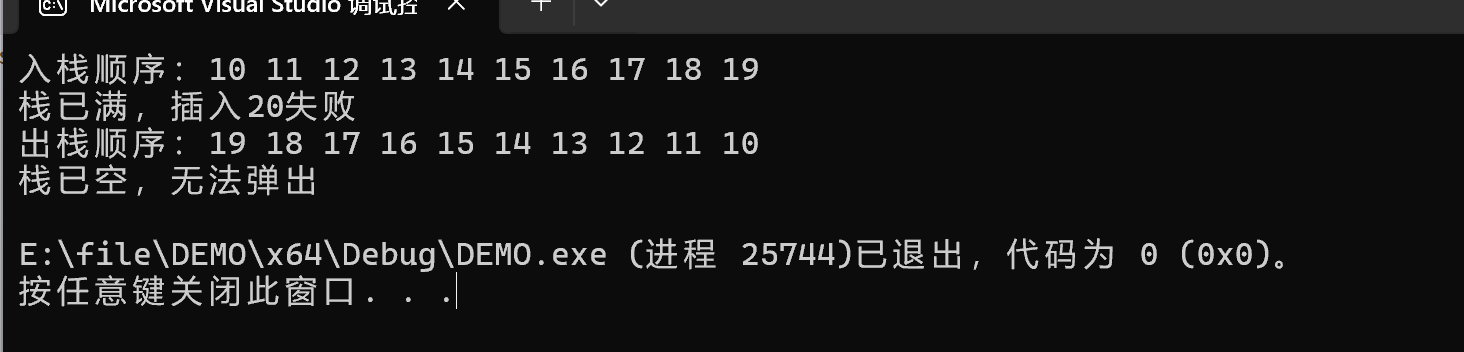
printf("入栈顺序：");
for (int i = 0; i < 10; i++)
{
stack_push(&s, i + 10); // 压入10~19
printf("%d ", i + 10);
}
printf("\n");
// 测试栈满
if (stack_push(&s, 20) == -1)
printf("栈已满，插入20失败\n");
// 3. 出栈测试
printf("出栈顺序：");
while (!stack_isemty(&s))
{
stack_pop(&s, &temp);
printf("%d ", temp);
}
printf("\n");
// 测试栈空
if (stack_pop(&s, &temp) == -1)
printf("栈已空，无法弹出\n");
// 4. 销毁栈
stack_destroy(&s);
return 0;
}

队列

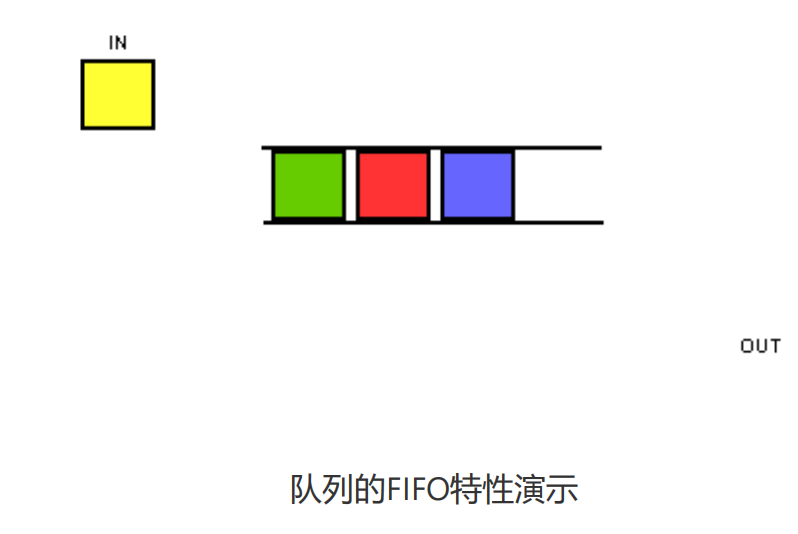
队列是一种逻辑结构，是特殊的线性表。特殊在：

只能在固定两端操作：一端插入（队尾），另一端删除（队头）

这种限制使队列呈现"先进先出/后进后出"（FIFO）的特性，就像现实中的排队：

银行排队：先来的客户先办理业务

打印队列：先提交的文档先被打印

消息队列：先到达的消息先被处理

术语定义

队头(Front)：允许删除的一端

队尾(Rear)：允许插入的一端

入队(Enqueue)：在队尾插入元素

出队(Dequeue)：从队头删除元素

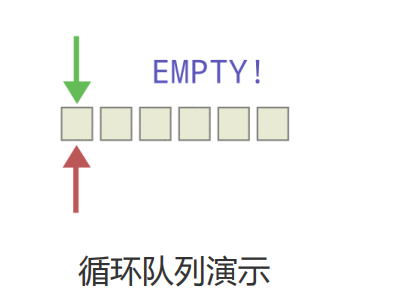
循环队列（数组实现）

使用数组存储，通过模运算实现循环利用空间：

// 队列元素类型
typedef int DATA;
// 循环队列结构体
typedef struct
{
DATA *data; // 存储数组
int size; // 队列容量
int front; // 队头下标（出队维护队头下标）
int rear; // 队尾下标（入队维护队尾下标）
}SQueue;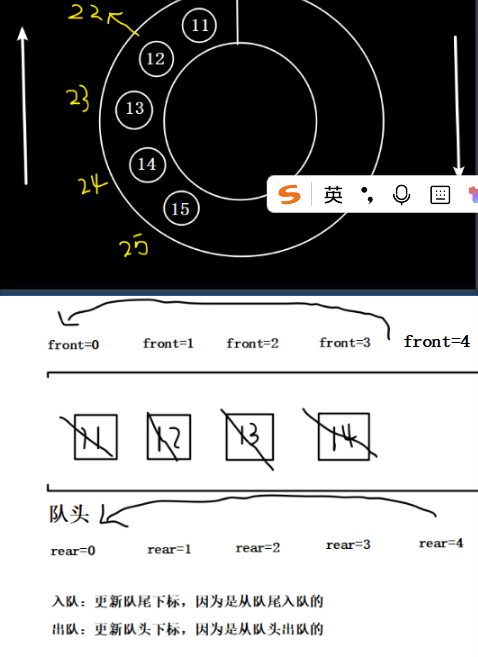

关键点：

1. 牺牲一个存储单元区分队空和队满

2. 队空条件：front == rear == -1

3. 队满条件：(rear+1)%size == front

4. 元素数：(rear-front+size)%size

#ifndef SQUENCE_QUEUE_H
#define SQUENCE_QUEUE_H
#include
#include
#include
typedef int DATA;
typedef struct {
DATA* data;//数据指针
int size; //队列容量
int front; //队头下标
int rear;// 对尾下标
}SQueue;
int squeue_init(SQueue* q, int size);//初始化
int squeue_isfull(SQueue* q);//判断队列是否已满
int squeue_isempty(SQueue* q);//判断队列是否为空
int squeue_entrance_queue(SQueue* q, DATA data);//入队
int squeue_dequeue_queue(SQueue* q, DATA* data);//出队
int squeue_destroy(SQueue* q);//销毁队列
#endif
#include "squence_queue.h"
int squeue_init(SQueue* q, int size) {
q->data = (DATA*)calloc(size, sizeof(DATA));
if (!q->data)
{
return -1;
}
q->size = size;
q->front = q->rear = 0;
return 1;
}
//跟随的时候比如2个人因为队头的下标比队尾要多一个元素
int squeue_isfull(SQueue* q) {
return (q->rear + 1) % q->size == q->front;
}
//只有一次的时候循环队列为空那就是队头跟队尾相等，因为本身队头下标要多出队尾下标一个
int squeue_isempty(SQueue* q) {
return q->rear == q->front;
}
//从队尾入数据
int squeue_entrance_queue(SQueue* q, DATA data) {
if (!q)return -1;
if (squeue_isfull(q)) return -1;
q->data[q->rear] = data;
q->rear = (q->rear + 1) % q->size;
return 1;
}
int squeue_dequeue_queue(SQueue* q, DATA* data) {
if (!q)return -1;
if (squeue_isempty(q)) return -1;
*data = q->data[q->front];
q->front = (q->front + 1) % q->size;
return 1;
}
int squeue_destroy(SQueue* q) {
if (!q)return -1;
if (q->data!=NULL)
{
free(q->data);
q->data = NULL;
}
q->front = q->rear = 0;
q->size = 0;
return 1;
}
#include "squence_queue.h"
int main() {
SQueue queue;
DATA temp;
squeue_init(&queue, 10);
//入队列
for (int i = 0; i < 10; i++)
{
squeue_entrance_queue(&queue, i + 1);
printf("%d ", i + 1);
}
printf("\n");
//出队列
while (!squeue_isempty(&queue)) {
squeue_dequeue_queue(&queue, &temp);
printf("%d ", temp);
}

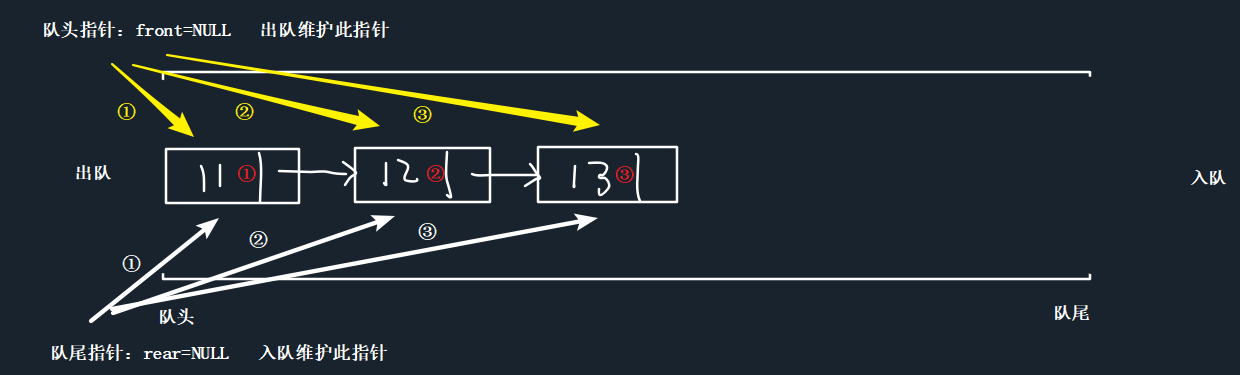
栈式队列（链表实现）

#ifndef  LINK_QUEUE_H
#define  LINK_QUEUE_H
#include
#include
#include
typedef int DATA;
//定义单链表
typedef struct node{
DATA  data;
struct node* next;
}NODE;
typedef struct {
NODE *front;//队头指针
NODE *rear;//队尾指针
int size;// 入队列的元素个数
int capacity;//队列的容量
}link_queue;
int link_queue_init(link_queue* q, int size);
int link_queue_isfull(link_queue* q);
int link_queue_isempty(link_queue* q);
int link_queue_entrance(link_queue* q,DATA data);
int link_queue_dequeue(link_queue* q, DATA *data);
int link_queue_destory(link_queue* q);
#endif
#include "link_queue.h"
int link_queue_init(link_queue* q, int size) {
if (!q) return -1;
q->front = q->rear = NULL;
q->size = 0;
q->capacity = size;
return 1;
}
int link_queue_isfull(link_queue* q) {
if (!q) return -1;
return q->size == q->capacity;
}
int link_queue_isempty(link_queue* q) {
if (!q) return -1;
return q->size == 0;
}
int link_queue_entrance(link_queue* q, DATA data) {
if (!q) return -1;
if (link_queue_isfull(q)) return -1;
//创建一个新节点
NODE* newNODE = (NODE*)malloc(sizeof(NODE));
if (newNODE == NULL) return -1;
newNODE->next = NULL;
newNODE->data = data;
//如果队列为空
if (link_queue_isempty(q))
{
q->front = q->rear = newNODE;
}
else
{
//如果队列不为空
q->rear->next = newNODE;
q->rear = newNODE;
}
q->size++;
return 1;
}
int link_queue_dequeue(link_queue* q, DATA* data) {
if (!q) return -1;
if (link_queue_isempty(q)) return -1;
//获取头指针
NODE* temp = q->front;
*data = temp->data;
q->front = temp->next;//更新头指针
//如果队列只有一个元素，出队后队列为空
if (q->front == NULL)
{
q->rear = NULL;
}
free(temp);
q->size--;
return 1;
}
int link_queue_destory(link_queue* q) {
DATA temp;
if (!q) return -1;
while (!link_queue_isempty(q)) {
link_queue_dequeue(q, &temp);
}
return 1;
}
#include "link_queue.h"
int main() {
link_queue q;
DATA temp;
// 1. 初始化容量为10的链式队列
link_queue_init(&q, 10);
// 2. 入队测试
printf("入队顺序：");
for (int i = 0; i < 10; i++)
{
link_queue_entrance(&q, i + 10); // 10~19
printf("%d ", i + 10);
}
printf("\n");
// 测试队满
if (link_queue_entrance(&q, 20) == -1)
printf("队列已满，插入20失败\n");
// 3. 出队测试
printf("出队顺序：");
while (!link_queue_isempty(&q))
{
link_queue_dequeue(&q, &temp);
printf("%d ", temp);
}
printf("\n");
// 测试队空
if (link_queue_dequeue(&q, &temp) == -1)
printf("队列已空，无法出队\n");
// 4. 销毁队列
link_queue_destory(&q);
return 0;
}

树

树是一种非线性结构，其严格定义：

除根节点外，每个节点有且仅有一个直接前驱

每个节点可以有零个或多个直接后继

这种特性称为一对多的逻辑关系

用于描述具有层次关系的数据结构，类似组织架构关系

树的组成：根节点、分支节点、叶子节点

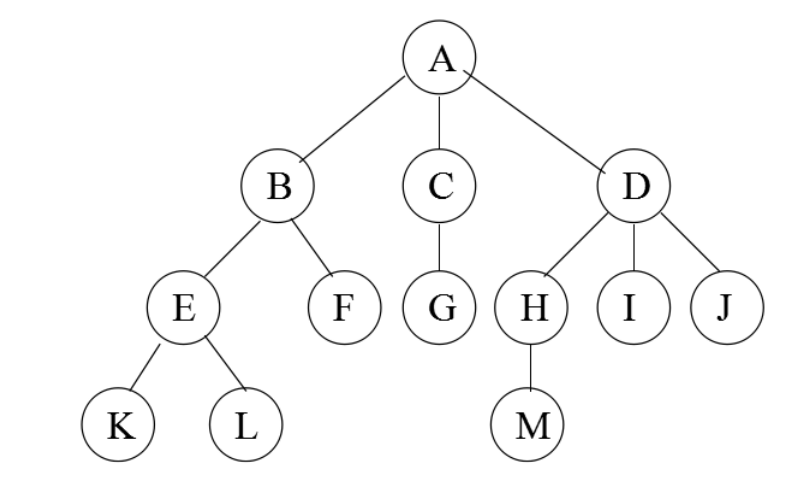
基本术语：

1. 结点：元素及其子树

2. 根节点(root)：第一个节点（如图中A）

3. 父节点(parent)：直接前驱（A是B的父节点）

4. 子节点(child)：直接后继（B、C、D是A的子节点）

5. 层次(level)：根为第1层，后代递增（E为第3层）

6. 度(degree)：子节点总数（B的度为2）

7. 叶子节点(leaf)：度为0的节点（K、L、F、G、M、I、J）

8. 高度/深度(height)：最大层次（图示树高为4）

9. 有序树与无序树：子节点有明确顺序的为有序树

二叉搜索树（BST）

根指针：指向根节点的指针变量

节点结构：

数据域（存储数据）

指针域（左、右子节点指针）

二叉树遍历

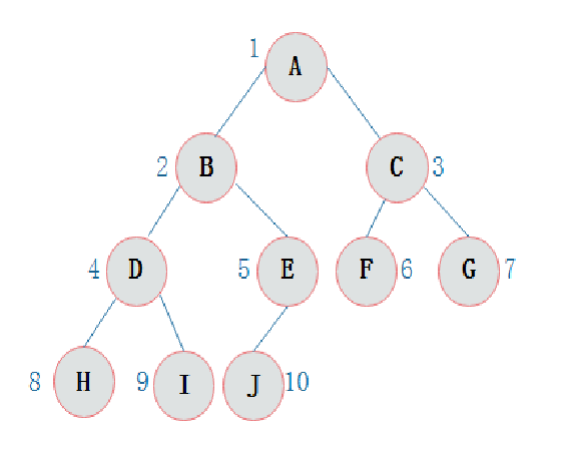
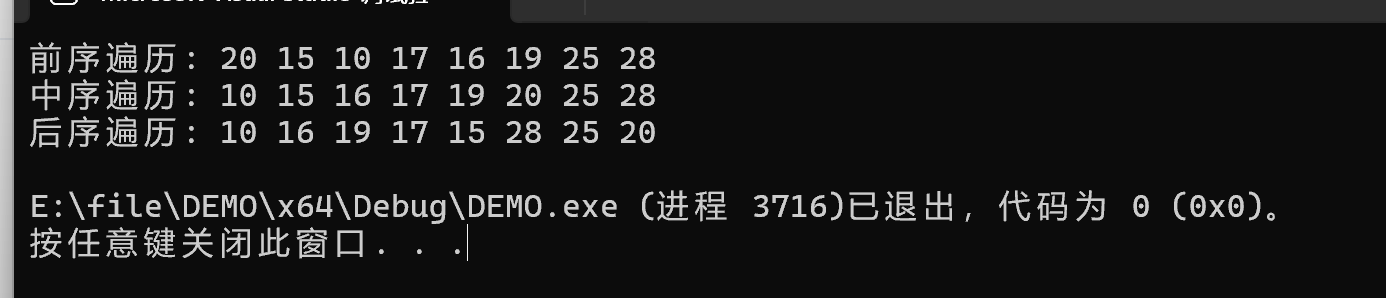
前序遍历（根左右）：A、B、D、H、I、E、J、C、F、G

中序遍历（左根右）：H、D、I、B、J、E、A、F、C、G

后序遍历（左右根）：H、I、D、J、E、B、F、G、C、A

插入节点

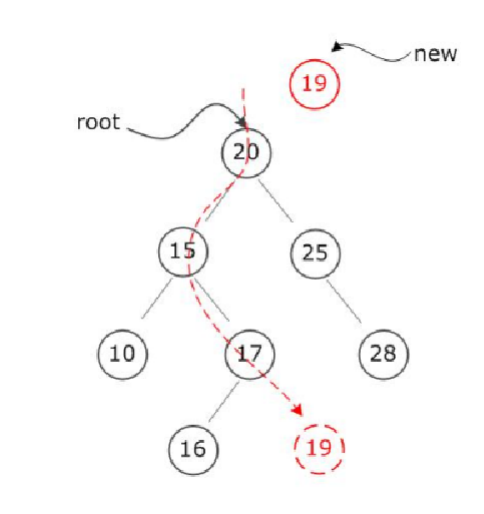
用递归遍历 前序遍历，根节点为空结束打印根，然后看左 左边节点为空结束打印左 右边节点为空结束打印右

最后后序遍历，左右都为空，先打印左，然后右边也是空结束，打印右，最后打印中间节点

#ifndef  BTREE_H
#define  BTREE_H
#include
#include
#include
typedef int DATA;
typedef struct bt_node {
DATA data;
struct bt_node* left;//左孩子
struct bt_node* right;//右孩子
}btree;
//初始化节点
int btree_create(btree** root, DATA data);
//前序遍历
void preorder(btree* root);
//中序遍历
void midorder(btree* root);
//后序遍历
void postorder(btree* root);
#endif
#include "btree.h"
//创建一个树，如果树存在，返回-1，不存在返回1
int btree_create(btree** root, DATA data) {
if (*root) return -1;
btree* newNODE = (btree*)malloc(sizeof(btree));
if (!newNODE)return -1;
newNODE->data = data;
newNODE->left = newNODE->right = NULL;
*root = newNODE;
return 1;
}
int btree_add(btree** root, DATA data) {
btree* newNODE = (btree*)malloc(sizeof(btree));
if (!newNODE) return -1;
// 初始化新节点
newNODE->data = data;
newNODE->left = NULL;
newNODE->right = NULL;
btree* p = *root, * q = NULL;
// 如果没有节点
if (!p) {
*root = newNODE;
return 1;
}
// 如果节点存在用指针尾随法q尾随p
while (p) {
q = p;
// 如果目标数据小于等于当前节点数据，放到左子树
if (memcmp(&data, &(p->data), sizeof(DATA)) left;
}
else {
p = p->right;
}
}
// 循环结束后，q指向要插入位置的父节点
if (memcmp(&data, &(q->data), sizeof(DATA)) left = newNODE;
}
else {
q->right = newNODE;
}
return 1;
}
//前序遍历
void preorder(btree* root) {
if (!root)return;
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
void midorder(btree* root) {
if (!root)return;
midorder(root->left);
printf("%d ", root->data);
midorder(root->right);
}
void postorder(btree* root) {
if (!root)return;
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
#include "btree.h"
int main() {
btree* root = NULL;
btree_create(&root, 20);
// 修正这里：应该是 DATA 数组，不是 btree 数组
DATA arr[] = { 15, 25, 10, 17, 28, 16, 19 };
int len = sizeof(arr) / sizeof(DATA);
for (int i = 0; i left);    调用 postorder(NULL)
postorder(节点2->right);    调用 postorder(NULL)
printf("%d", 节点2->data);  打印 2 ← 这里打印的是节点2！
}

http://www.hskmm.com/?act=detail&tid=12075

相关文章：

  • 深入解析：【ubuntu】ubuntu中找不到串口设备问题排查
  • 酵母双杂交技术：高通量筛选的突破与不可忽视的三大局限性
  • ubuntu20.04测试cuda
  • Android Studio 配置国内源
  • PyCharm项目上传GitHub仓库（笔记） - 教程
  • 从RAG出发
  • 软件工程第二次作业——第一次个人编程作业
  • Ubuntu 24.04 安装 DaVinci Resolve
  • Promise中处理请求超时问题
  • 图解26：老生常谈的OSI网络模型
  • 【C++】指针
  • AI驱动建筑行业数字化转型
  • 详细介绍：前端学习——CSS
  • VSCode 把代码发送到激活状态下的终端
  • 线性结构之数组[基于郝斌课程]
  • 完整教程：Vue中的props方式
  • 图解25：MySQL主从复制原理
  • 用 Go 编写验证码识别脚本（基于 Tesseract）
  • 软工第二次作业
  • Zero-Shot、One-Shot、Few-Shot概念
  • ADS放入元器件include和DK.zip文件依然提示未定义
  • AI元人文（十三）：良知觉醒——论三值伦理模型与元道德主体的诞生
  • 「MCOI-05」魔仙
  • BlueHat v18 会议资料现已发布：前沿安全技术与漏洞缓解策略
  • label和brand的区别（品牌=brand？错了，你们的英语都学错了！）
  • 2025.9.21——1绿
  • 故障处理：ORA-04031真实案例分享
  • 图解24：8种常用的缓存淘汰策略
  • 读书笔记：更智能的数据库索引：只关注你需要的数据
  • JS设计模式-模块模式