其实标题指的是博弈论。
[AGC002E] Candy Piles
桌子上有 \(N\) 堆糖果。每堆糖果有 \(a_i\) 颗糖果。
Snuke 和 Ciel 正在玩游戏。他们轮流走。Snuke 先走。在每个回合中,当前玩家必须执行以下两个操作之一:
- 选择剩余糖果数量最多的一堆,然后吃掉那堆糖果中的所有糖果。
- 从每堆剩下的一颗或多颗糖果中,吃一颗糖果。
吃了桌上最后一块糖的玩家输掉了比赛。确定如果两个玩家都以最佳方式玩游戏,哪个玩家会赢。
sol
牛逼题目。
你可以先把石子的个数从大到小排序,如下图。

转化成网格图就是
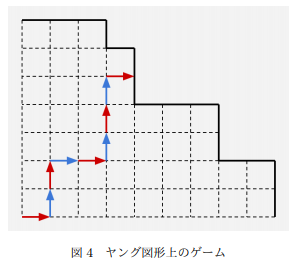
那么上面的实线就是必败点,我们相当于每次往右走或者往上走 (相当于吃一堆或者全部吃一颗)。
那么向上走和向右走都是必败点的点就是必胜点,反之就是必败点,画出来长这样(O 为必败):
 。
。
注意到一个对角线都是一样的,所以我们直接找到一个最大的正方形使得其够不着边界。
然后直接设其右上方顶点为 (i,i) 。当它到最上面且不在边界上的点的距离和最右面且不在边界上的点的距离其中一个为奇数时,这个点为必败点,反之这个点为必胜点。
CF794E Choosing Carrot
下个月就是奶牛Z的生日啦,为了给奶牛Z购买生日礼物,奶牛A和奶牛B决定去挑选奶牛Z最喜欢的青草来作为送给奶牛Z的生日礼物。
现在,奶牛A和奶牛B买来了n堆青草,从左数起,第i堆青草的甜度为ai。奶牛A认为奶牛Z喜欢甜的青草,而奶牛B认为奶牛Z喜欢不甜的青草。因此,奶牛A希望选出来的青草是最甜的,奶牛B希望选出来的是最不甜的青草。
为了解决这个问题,奶牛A与奶牛B决定玩一个游戏,他们俩每次可以从两端的青草开始,选择其中一堆并把这一堆青草吃掉,最后剩下的那一堆青草就是送给奶牛Z的生日礼物,奶牛A先开始吃。
在玩游戏之前,奶牛B去上了一次厕所,奶牛A乘机进行了K次操作,每次操作也是按照要求从这些草堆当中,选择两端的草堆并吃掉其中一堆。在奶牛B回来之后,同样也是奶牛A先开始吃。
奶牛A想知道,对于每一个K(0≤K≤n-1),最后送给奶牛Z的青草甜度分别是多少?
sol
最简单。
讨论 \(k=0\) 的情况:
设 \(mid=(n+1)/2\)。
奇数的答案是 \(\max(\min(a_{mid},a_{mid-1}),\min(a_{mid},a_{mid+1}))\)。
偶数的答案是 \(\max(a_{mid},a_{mid-1})\)。
然后对于这个 \(k\) 的不同,相当于就是把区间增长了,反正写个 st 表当 rmq 做就行了。
[ARC116F] Deque Game
给定 \(K\) 个数列。第 \(i\) 个数列 \(A_i\) 的长度为 \(N_i\)。
高桥君和青木君将用这些数列进行游戏。直到所有数列都变为长度 \(1\),高桥君和青木君轮流进行以下操作:
- 选择一个长度至少为 \(2\) 的数列,删除其第一个元素或最后一个元素。
高桥君先手。高桥君希望最大化最后剩下的 \(K\) 个元素的总和,青木君则希望最小化该总和。
当双方都采取最优策略时,请输出最后剩下的 \(K\) 个元素的总和。
sol
困难至极。
发现当 \(k=1\) 时跟上面的是一样的,所以奇偶数的讨论可以直接扔过来。
当这个队列长度为奇数时,且先手先手时,答案是 \(\min(\max(a_{mid},a_{mid-1}),a_{mid}) \leq a_{mid}\)。
当这个队列长度为奇数时,且先手后手时,答案是 \(\max(\min(a_{mid},a_{mid-1}),a_{mid}) \geq a_{mid}\)。
所以在这个奇数的情况下先手更优一点。
然后你考虑偶数的情况,偶数是先手更优一些。
所以他们两个会优先把偶数给吃完,然后再吃奇数。
但是偶数每吃掉一个会导致先后手置换,所以你需要按照这个的 先手答案 - 后手答案排序去吃,这样一定是最优的。
然后你再去吃奇数,这个不会换先后手顺序,直接算就好了。
[AGC010D] Decrementing
黑板上写有 \(N\) 个整数。第 \(i\) 个整数为 \(A_i\),这些数的最大公约数为 \(1\)。
高桥君和青木君用这些数进行游戏。游戏由高桥君先手,双方轮流进行如下操作:
- 从黑板上选择一个大于等于 \(2\) 的数,将其减去 \(1\)。
- 然后,计算黑板上所有数的最大公约数 \(g\),并将所有数都除以 \(g\)。
当黑板上所有数都变为 \(1\),且无法再进行操作时,无法操作的一方判负。假设双方都采取最优策略,问哪一方会获胜。
sol
儿子题目。
算 \(\sum_{i=1}^N (A_i-1)\),如果没有除去最大公约数的话就是看奇偶性,奇数先手必胜。
但是现在有这个除法了,不难发现只有除去 \(2\) 的倍数才能改变奇偶性,所以说看什么情况才能除去 \(2\)。
发现除去 2 的情况当且仅当只有一个奇数,遇到这种情况递归处理就好了。
