Figure 1:直达声在 t = 0 的冲激
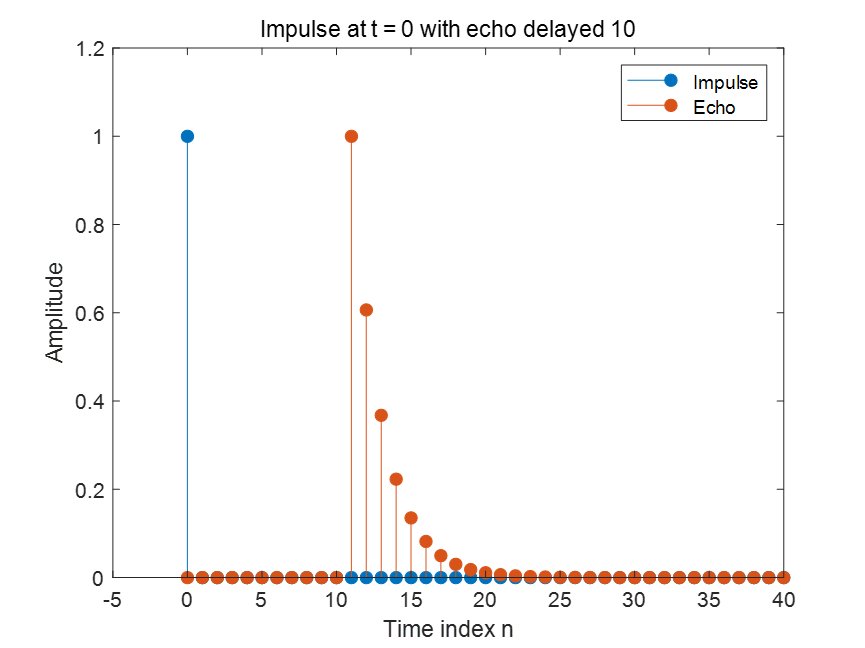
在房间内,假设在 t = 0 时刻有一个强度为 1 的冲激信号(蓝色)。
由于房间存在反射,当声音传播一段时间(例如 延迟 10 个时刻)后,会在 t = 10 左右接收到第一个反射声(红色)。
随着时间推移,反射声的强度按指数衰减(这里用 exp(-at) 表示),这条红色曲线便是房间的冲激响应(Impulse Response),它描述了系统对单位冲激的全部响应。
Figure 2:直达声在 t = 5,强度为 0.8 的冲激
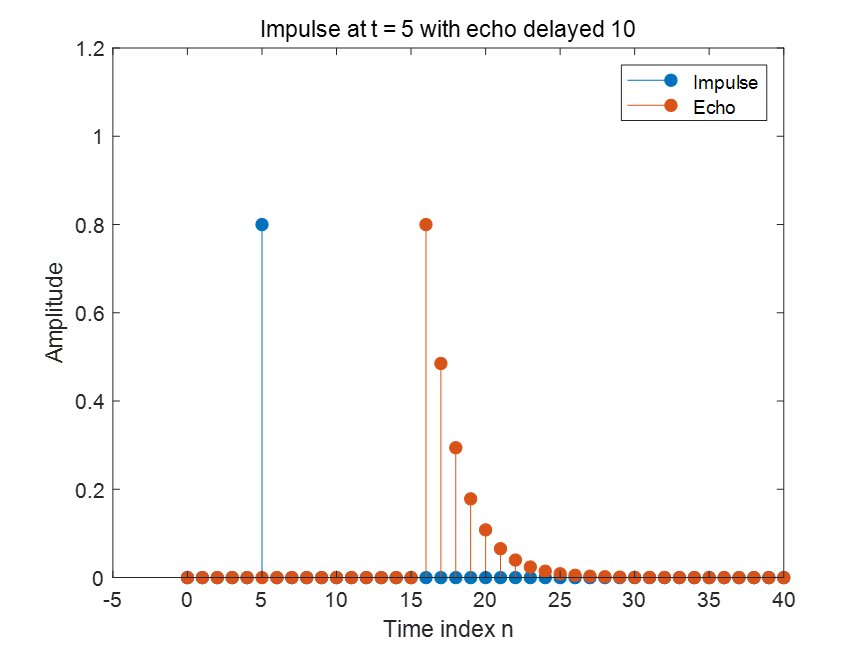
同理,当冲激信号(蓝色)延迟到 t = 5 时刻出现,强度为 0.8,
房间的反射声也相应延迟了 10 个时刻,在 t = 15 附近 才开始出现,且强度衰减到原来的 0.8 倍。
这说明系统是线性时不变的(LTI):延迟输入信号的时间,也只会让响应整体延迟相同的时间。
Figure 3:叠加两个冲激的响应
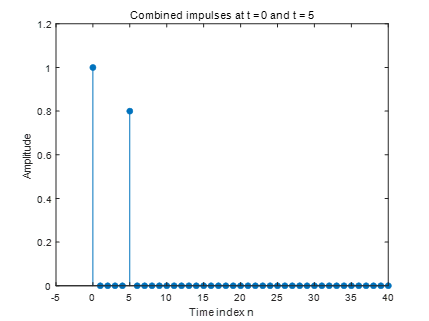
当两个冲激(t = 0 的蓝色脉冲和 t = 5 的蓝色脉冲)同时存在时,
系统的总响应就是这两个单独冲激响应的线性叠加(左图)。
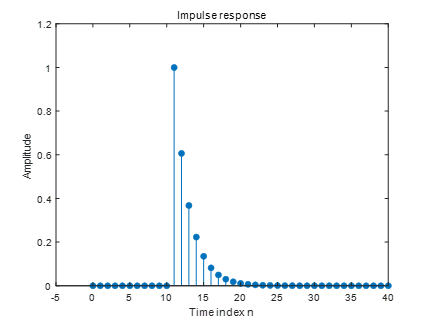
得到的房间反射声(下图红色)即输入信号(左上图)与房间脉冲响应(右上图)卷积的结果:
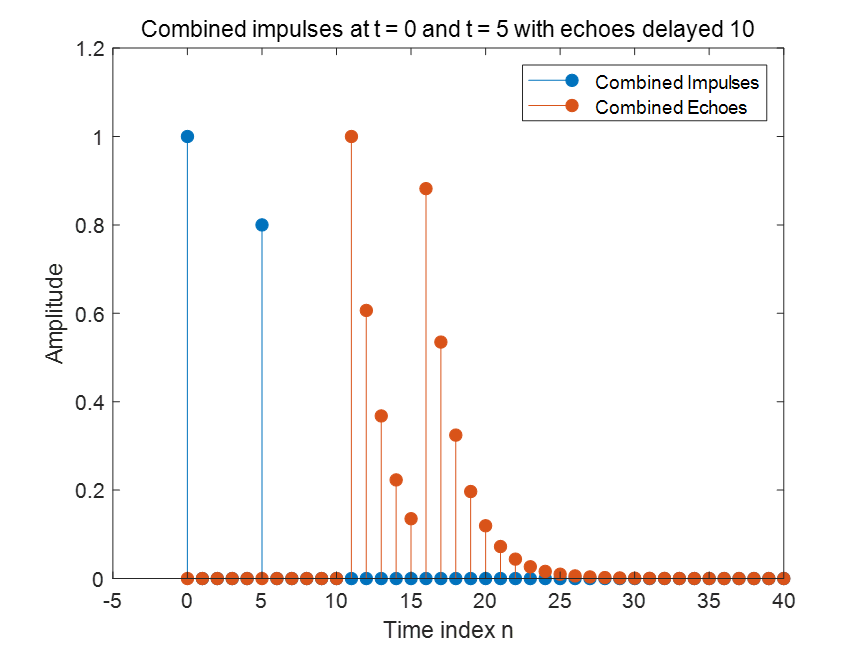
这正是卷积的核心思想:
系统的输出 = 输入信号的每个冲激 × 系统对冲激的响应,再全部叠加。
Figure 4:随机激励信号 u[n]
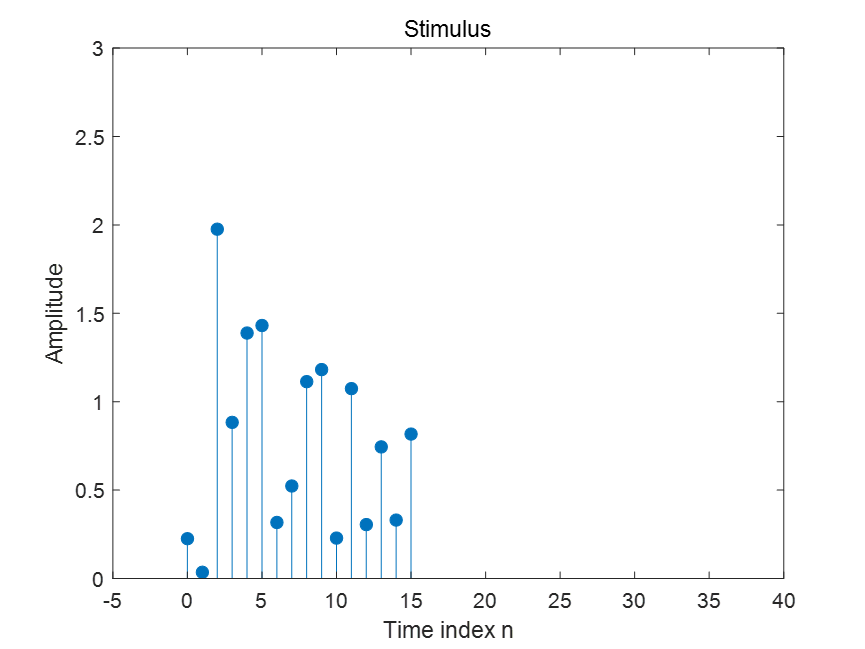
现在我们不再输入单一冲激,而是输入一段 t = 0 ~ 15 的复杂随机信号(蓝色)。
可以把它看成由许多不同时刻、不同幅度的小冲激组成的序列。
每个小冲激都会激发出一个“缩放后、延迟后”的房间冲激响应,所有这些响应叠加起来,形成完整的输出信号。
Figure 5:手动叠加卷积 vs MATLAB conv函数
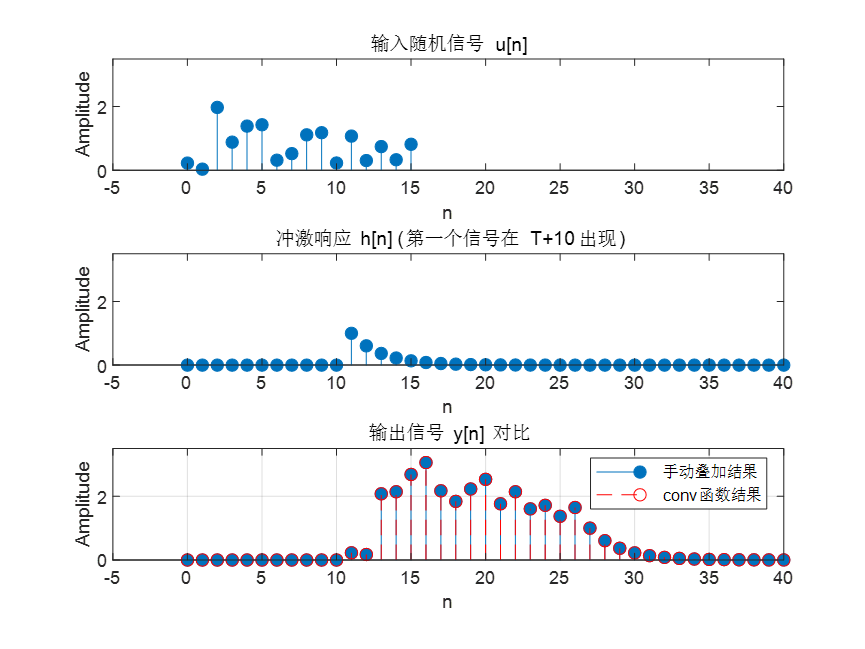
我们将随机信号拆分成若干个单位冲激,对每个冲激与 h[n] 卷积后叠加,得到手动卷积结果(第三个图蓝色)。
然后再用 MATLAB 内置的 conv 函数计算标准离散卷积(第三个图红色虚线)。
两者完全重合,验证了“逐个冲激叠加”的卷积定义确实与数学公式一致。
这就是卷积的本质:
输入信号中每个采样值,都会触发一个对应的冲激响应,输出信号就是这些响应的叠加。
最终得到的红色曲线就是系统对复杂激励的输出信号 y[n]。
它等价于输入信号与房间冲激响应的卷积结果。
理解离散卷积后,再推广到连续时间,就能自然理解声学、信号处理中常见的卷积积分。
所有图的代码如下:
clear; clc;%% ================== 回声模拟 1:直达声在 t=0 ==================
n1 = 0:40; % 时间索引
u1 = zeros(size(n1)); % 原始信号
u1(1) = 1; % 直达声在 t=0% 回声参数
echo_delay1 = 10; % 回声延迟
echo_start1 = echo_delay1 + 1; % 回声开始时间索引
echo_amp1 = max(u1); % 回声初始强度
a1 = 0.5; % 衰减系数% 添加回声
y1 = u1; % 初始化输出
for t = echo_start1:length(n1)-1y1(t+1) = y1(t+1) + echo_amp1 * exp(-a1 * (t - echo_start1));
end% 绘图
figure;
stem(n1, u1, 'filled'); hold on; % 直达声
stem(n1, y1 - u1, 'filled'); hold off; % 回声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 1.2]);
title('Impulse at t = 0 with echo delayed 10');
legend('Impulse', 'Echo');%% ================== 回声模拟 2:直达声在 t=5,强度为 0.8 ==================
n2 = 0:40; % 时间索引
u2 = zeros(size(n2)); % 原始信号
T = 5; % 直达声时间
u2(T+1) = 0.8; % MATLAB 索引从 1 开始% 回声参数
echo_delay2 = 10; % 回声延迟
echo_start2 = T + echo_delay2 + 1; % 回声开始时间索引
echo_amp2 = 0.8; % 回声初始强度
a2 = 0.5; % 衰减系数% 添加回声
y2 = u2; % 初始化输出
for t = echo_start2:length(n2)-1y2(t+1) = y2(t+1) + echo_amp2 * exp(-a2 * (t - echo_start2));
end% 绘图
figure;
stem(n2, u2, 'filled'); hold on; % 直达声
stem(n2, y2 - u2, 'filled'); hold off; % 回声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 1.2]);
title(['Impulse at t = ', num2str(T), ' with echo delayed 10']);
legend('Impulse', 'Echo');%% ================== 回声模拟 3:叠加信号(t=0 与 t=5) ==================
% 将两组激励与回声叠加
n_total = n1; % 时间索引一致
u_total = u1 + u2; % 叠加直达声
y_total = y1 + y2; % 叠加回声响应% 绘图
figure;
stem(n_total, u_total, 'filled'); hold on; % 总直达声
stem(n_total, y_total - u_total, 'filled'); hold off;% 总回声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 1.2]);
title('Combined impulses at t = 0 and t = 5 with echoes delayed 10');
legend('Combined Impulses', 'Combined Echoes');% 绘图
figure;
stem(n_total, y1 - u1, 'filled'); hold on; % 总直达声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 1.2]);
title('Impulse response');%% ================== 回声模拟 4:随机信号卷积验证 ==================T = 15; % 信号长度为 T+1
n3 = 0:T; % 时间索引
u_rand = abs(randn(1, length(n3))); % 随机输入信号(非负)figure;
stem(n3, u_rand, 'filled'); hold on; % 总直达声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 3]);
title('Stimulus');% ===== 假设系统的冲激响应 h[n](可替换为真实测得的 y1-u1) =====
% 这里举例假设冲激响应从第10个采样开始
h = y1 - u1; % 延迟10采样,模拟“第一个回声在T+10时刻出现”
Lh = length(h);% ===== 手动卷积:逐个冲激叠加 =====
y_manual = zeros(1, length(u_rand) + Lh - 1); % 预分配输出长度
for n = 1:length(u_rand)% 当前冲激输入信号(只有一个采样非零)delta = zeros(1, length(u_rand));delta(n) = u_rand(n);% 当前冲激响应的输出(延迟叠加)y_curr = conv(delta, h);% 累加所有冲激响应y_manual = y_manual + y_curr;
end% ===== 用 MATLAB 内置卷积函数验证 =====
y_conv = conv(u_rand, h);% ===== 绘图比较 =====
figure;
subplot(3,1,1);
stem(n3, u_rand, 'filled');
title('输入随机信号 u[n]');
xlabel('n'); ylabel('Amplitude');axis([-5 40 0 3.5]);subplot(3,1,2);
stem(0:length(h)-1, h, 'filled');
title('冲激响应 h[n] (第一个信号在 T+10 出现)');
xlabel('n'); ylabel('Amplitude');axis([-5 40 0 3.5]);subplot(3,1,3);
stem(0:length(y_manual)-1, y_manual, 'filled'); hold on;
stem(0:length(y_conv)-1, y_conv, 'r--');
legend('手动叠加结果','conv函数结果');
title('输出信号 y[n] 对比');
xlabel('n'); ylabel('Amplitude');
grid on;
axis([-5 40 0 3.5]);figure;
stem(0:length(y_manual)-1, y_manual, 'filled'); hold on; % 总直达声
xlabel('Time index n');
ylabel('Amplitude');
axis([-5 40 0 3]);
title('Stimulus');
