很拗口的名字,其情景是这样的:
我们有一个点 \(B(n,m)\),需要求原点 \(A\) 到这个点的路径条数(限制只能向右、上走)。
平凡的题目做法很简单,我们一共走 \(n+m\) 步,其中 \(n\) 步向右,方案数 \(\binom {n + m} n\)。
但是进阶版的题目会给出一些限制,比如给出两条直线,要求不能碰到这两条直线。
如下图:\(n=6,m=3\),不能碰到 \(l_1:y=x+1,l_2:y=x-4\)。那么我们的路径有以下可能,箭头表示方向。
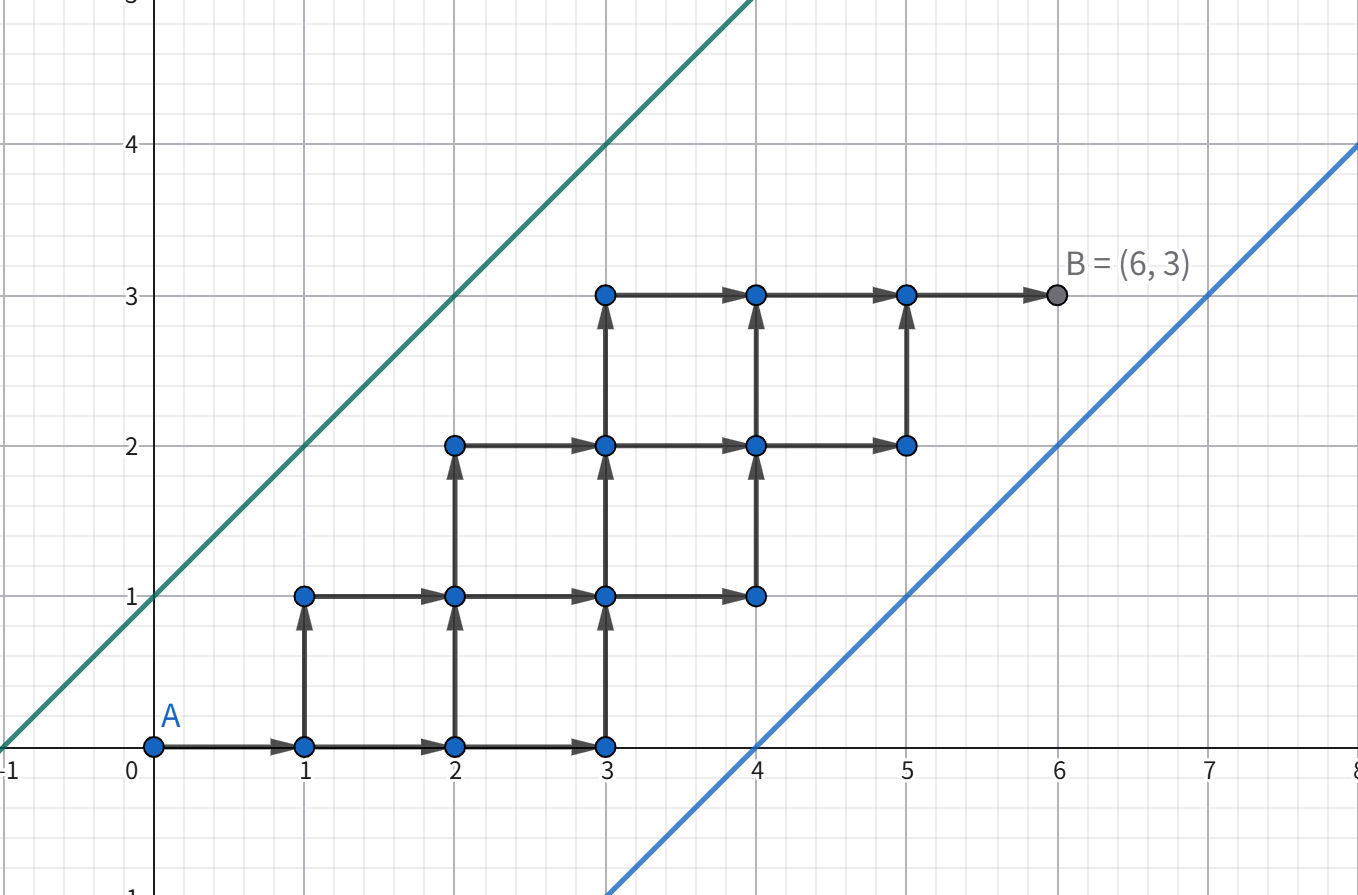
Part 1
我们正难则反,考虑容斥,扔掉那些碰到 \(l_1, l_2\) 的路径,从简单入手,先考虑碰到 \(l_1\) 的直线,如图中黑色线:

但这个碰到 \(l_1\) 太神秘了,而且原点和 \((n,m)\) 都在一侧,这让我们很难办,那我们如果有一个在 \(l_1\) 上方的点,此时,我们一条从原点到这个点的路线一定是经过 \(l_1\) 的。
我们考虑将碰到 \(l_1\) 的直线与这样的路径相对应,或者说用这种路径来生成所需路径。
我们发现,我们将原本路径从第一次碰到 \(l_1\)以后的部分都关于 \(l_1\) 做翻折(这个是否第一次不重要,只需要固定一个位置开始翻),形成图中紫色路径。那么,得到的路径终点为 \(B\) 关于 \(l_1\) 的对称点 \(B'\),我们发现这是一个一一映射,也就是只需要对原点到 \(B'\) 的路径计数即可,这同我们开始提到的平凡做法。
只碰到 \(l_2\) 直线同理,将 \(B\) 关于 \(l_2\) 对称得到 \(C\) 即可。
我们成功地分别算出了碰到 \(l_1\) 和 \(l_2\) 的方案数。
Part 2
我们定义一个序列,\(1212122211121 \cdots\) 表示路径碰到两条线的整个顺序。那么我们现在可以分别计算出序列中含有 \(1\)、含有 \(2\) 的个数了。同时,我们发现连续经过一条直线多次的情况已经被涵盖,那么下文讨论的序列都是将连续的 \(1\) 或 \(2\) 缩成一个之后的序列。
令 \(f(S)\) 碰线序列包含子串 \(S\) 的序列集合。答案应为:总情况数 - 碰到 \(l_1\) - 碰到 \(l_2\) + 既碰到 \(l_1\) 又碰到 \(l_2\)。即:
以此类推,每次拆开最后一项,那么最终得到:
也就是说我们需要算出所有的 \(f(s)\),其中 \(s\) 是一个 \(1\)、\(2\) 交替的序列。
Part 3
依旧从简单入手,我们考虑从 \(f(1,2)\) 开始算,并推广。
我们考虑刻画这种情形,如下图:
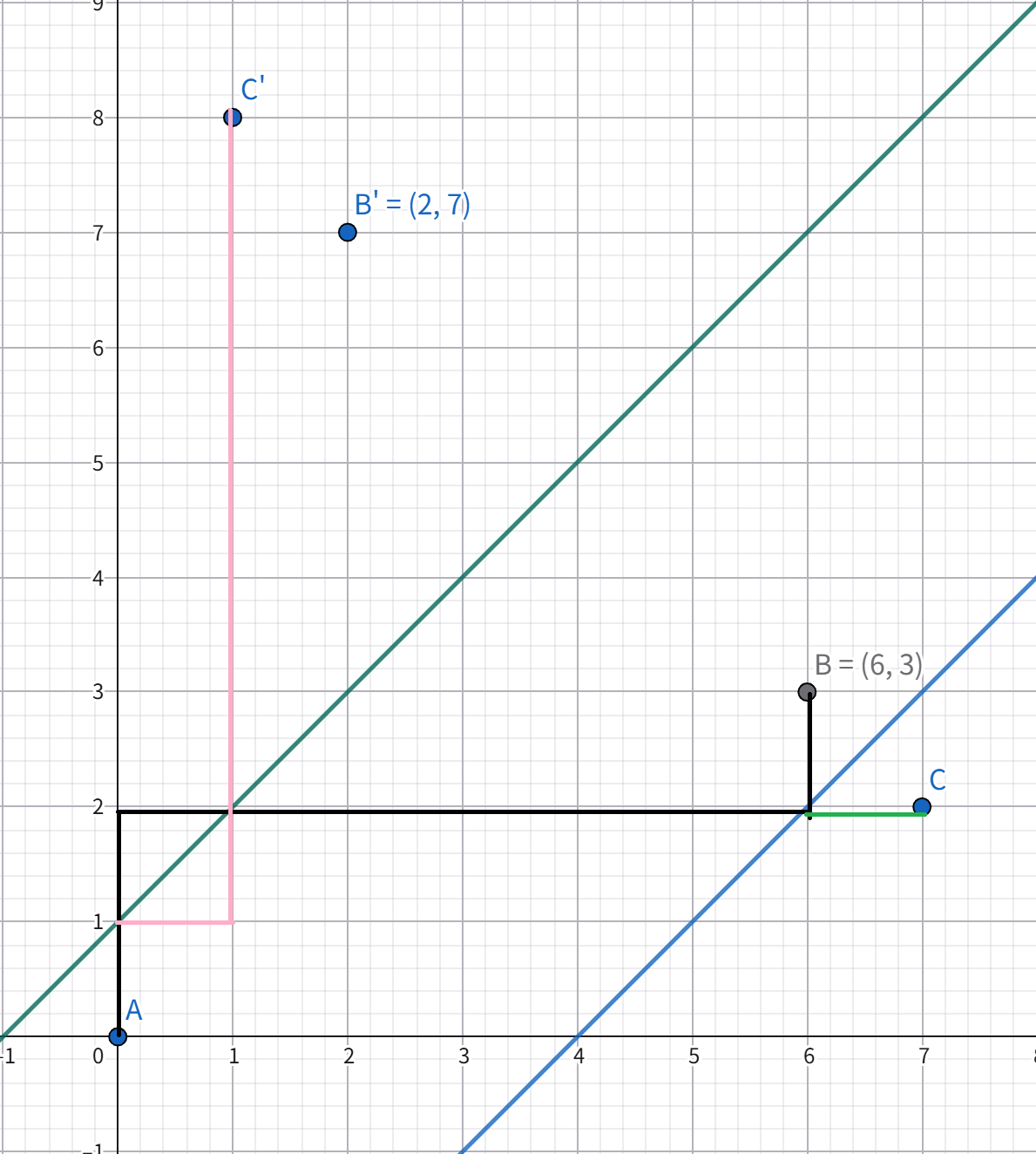
这是一个先经过 \(l_1\) 后经过 \(l_2\) 的路径,类似地,(但是注意要倒着来,可以解释为“生成”操作的逆)我们先将其对 \(l_2\) 对称(绿色),再对 \(l_1\) 对称(粉色),得到一个从原点到 \(C'\)(\(C'\) 为 \(C\) 关于 \(l_1\) 的对称点)的路径,这也是好算的。
那么可以推广出一个 \(f(s)\) 的算法,即我们倒序枚举 \(i\),将 \(B\) 关于 \(l_{s_i}\) 翻折。这样得到最后的点后用 \(\binom {x+y} x\) 即可算出。
Part 4
总结一下算法流程。
因为我们算 \(f(s)\) 要从后往前算,那么我们干脆直接从后往前来拆。
我们分两种情况,分别是 \(s\) 序列最后一位是 \(1\) 或 \(2\)。
对于最后一位是 \(1\) 的所有 \(s\):
-
我们将当前点按照 \(l_1\) 翻折,得到的点 \((x,y)\),将 \((x,y)\) 的贡献乘上系数 \(-1\) 加入答案。
-
我们再将其按照 \(l_2\) 翻折,得到的 \((x',y')\) 贡献,乘上系数 \(1\) 加入答案。
-
在 \((x,y)\) 不到第二、三、四象限的条件下重复以上步骤。
(系数是由 Part 2 的容斥式子中 \(|s|\) 决定的)
这样我们可以扫一遍算出所有最后一位是 \(1\) 的 \(s\) 的贡献。
那么对于最后一位是 \(2\) 的也类似,只是交换 \(l_1,l_2\) 的位置。
Part 5
分析一下复杂度,发现我们的复杂度由翻折的次数决定。
我们发现,每次翻折都至少使得 \(\min(x,y)\) 减少 \(1\),那么复杂度是 \(O(\min(x,y))\)。
