当前位置：首页 > news >正文

解码数据结构栈

news 2025/9/27 16:26:00

栈的概念与特性

栈是线性结构的特殊形式，其设计初衷是解决 “数据需按特定顺序存取” 的场景（如函数调用、括号匹配），核心遵循 “后进先出”（LIFO，Last In First Out）原则，是计算机领域中最基础的数据结构之一。

关键定义与术语

术语	定义
栈（Stack）	仅允许在一端进行数据插入（入栈）和删除（出栈）的线性表
栈底（Bottom）	栈的封闭端，数据一旦入栈后，只有栈顶元素全部出栈后才能被访问
栈顶（Top）	栈的开放端，所有入栈、出栈操作均在此端进行，栈顶元素始终是 “最新入栈” 的数据
空栈	不包含任何元素的栈，此时栈顶指针（或下标）指向栈底外侧（如顺序栈 Top=-1）

核心操作

栈的基本操作需满足 “仅操作栈顶” 的约束，所有操作的时间复杂度均为O(1)（遍历除外，O (n)），具体如下：

操作名称	功能描述	关键约束
初始化（Init）	创建空栈，并为栈的管理结构（如结构体）分配内存，初始化栈底、栈顶、容量等参数	确保内存分配成功（避免空指针）
入栈（Push）	将数据插入栈顶，更新栈顶指针（或下标）	入栈前需判满（仅顺序栈需判满）
出栈（Pop）	移除栈顶数据，返回该数据，更新栈顶指针（或下标）	出栈前需判空
判空（IsEmpty）	判断栈是否为空（如顺序栈 Top=-1，链式栈栈顶指针为 NULL）	无
判满（IsFull）	仅顺序栈需实现，判断栈顶是否达到数组容量上限（Top=Size-1）	链式栈无需判满（动态分配）
取栈顶（GetTop）	返回栈顶数据，但不删除该数据	需先判空
遍历（Print）	从栈底到栈顶输出所有元素	无
销毁（Destroy）	释放栈占用的内存（顺序栈释放数组 + 管理结构体，链式栈释放所有节点 + 栈顶指针）	避免内存泄漏

栈的两种实现方式

栈作为线性表，可基于数组（顺序栈） 或单链表（链式栈） 实现。

顺序栈

核心原理
- 用连续数组存储数据，数组下标 0 为栈底，栈顶随数据插入 / 删除动态移动（Top 初始化为 - 1，代表空栈）。
- 需用结构体管理关键参数：栈底地址（数组指针）、栈容量（数组大小）、栈顶下标（Top）。
定义

typedef int DataType_t;
// 2. 定义顺序栈管理结构体
typedef struct SequenceStack {DataType_t *Bottom;  // 栈底地址（指向数组首元素）unsigned int Size;   // 栈容量（数组最大存储元素个数）int Top;             // 栈顶下标（空栈时为-1，栈满时为Size-1）
} SeqStack_t;

初始化

SeqStack_t *SeqStack_Init(unsigned int size) {// 分配管理结构体内存SeqStack_t *Manager = (SeqStack_t *)malloc(sizeof(SeqStack_t));if (Manager == NULL) {printf("Memory allocation failed for Manager!\n");return NULL;}// 分配栈数组内存Manager->Bottom = (DataType_t *)malloc(size * sizeof(DataType_t));if (Manager->Bottom == NULL) {printf("Memory allocation failed for Stack Array!\n");free(Manager);  // 先释放管理结构体，避免内存泄漏return NULL;}// 初始化参数Manager->Size = size;Manager->Top = -1;  // 空栈标志return Manager;
}

判空

bool SeqStack_IsEmpty(SeqStack_t *Manager) {return Manager->Top == -1;
}

判满

bool SeqStack_IsFull(SeqStack_t *Manager) {return Manager->Top == Manager->Size - 1;
}

入栈

bool SeqStack_Push(SeqStack_t *Manager, DataType_t data) {// 先判满if (SeqStack_IsFull(Manager)) {printf("Stack is full! Push failed.\n");return false;}Manager->Top++;          // 栈顶上移Manager->Bottom[Manager->Top] = data;  // 存入数据return true;
}

出栈

DataType_t SeqStack_Pop(SeqStack_t *Manager) {// 先判空if (SeqStack_IsEmpty(Manager)) {printf("Stack is empty! Pop failed.\n");return 0;  // 此处0为默认值，实际可通过返回bool+输出参数优化}DataType_t topData = Manager->Bottom[Manager->Top];  // 保存栈顶数据Manager->Top--;  // 栈顶下移（逻辑删除，无需真删除数据）return topData;
}

取栈顶元素

DataType_t SeqStack_GetTop(SeqStack_t *Manager) {if (SeqStack_IsEmpty(Manager)) {printf("Stack is empty! GetTop failed.\n");return 0;}return Manager->Bottom[Manager->Top];
}

遍历栈(栈底到栈顶)

void SeqStack_Print(SeqStack_t *Manager) {if (SeqStack_IsEmpty(Manager)) {printf("Stack is empty!\n");return;}printf("Stack Elements (Bottom -> Top): ");for (int i = 0; i <= Manager->Top; i++) {printf("%d ", Manager->Bottom[i]);}printf("\n");
}

销毁

// 二级指针销毁函数 避免野指针
void SeqStack_Destroy(SeqStack_t **Manager) {// 先判断二级指针和目标指针是否有效if (Manager == NULL || *Manager == NULL) {return;  // 避免对空指针解引用}// 释放内部数组if ((*Manager)->Bottom != NULL) {free((*Manager)->Bottom);(*Manager)->Bottom = NULL;}// 释放管理结构体free(*Manager);*Manager = NULL;  // 关键：直接将外部指针置为NULL
}

注：

顺序栈的容量固定，若需动态扩容，可在判满后重新分配更大数组（如原容量 2 倍），拷贝原数据后释放旧数组。
入栈 / 出栈仅操作栈顶，时间复杂度 O (1)；遍历需遍历所有元素，时间复杂度 O (n)。

链式栈

核心原理
- 用单链表存储数据，链表头部作为栈顶（头插法入栈、头删法出栈，操作更高效），无需固定容量（动态分配节点）。
- 仅需一个栈顶指针（指向链表首节点），空栈时栈顶指针为 NULL（无需栈底指针，链表尾节点即为栈底）。
定义

typedef int DataType_t;
typedef struct LinkStackNode {DataType_t data;                // 节点数据struct LinkStackNode *next;     // 指向下一节点的指针
} LinkStackNode;

初始化

LinkStackNode *LinkStack_Init() {return NULL;  // 空栈标志：栈顶指针为NULL
}

判空

bool LinkStack_IsEmpty(LinkStackNode *top) {return top == NULL;
}

入栈

// 入栈（头插法：新节点作为新栈顶）
LinkStackNode *LinkStack_Push(LinkStackNode *top, DataType_t data) {// 创建新节点LinkStackNode *newNode = (LinkStackNode *)malloc(sizeof(LinkStackNode));if (newNode == NULL) {printf("Memory allocation failed for new node!\n");return top;  // 入栈失败，返回原栈顶}// 新节点指向原栈顶newNode->data = data;newNode->next = top;// 新节点成为新栈顶return newNode;
}

出栈

//  出栈（头删法：删除栈顶节点，返回新栈顶）
LinkStackNode *LinkStack_Pop(LinkStackNode *top, DataType_t *outData) {// 先判空if (LinkStack_IsEmpty(top)) {printf("Stack is empty! Pop failed.\n");*outData = 0;return top;}// 保存原栈顶节点和数据LinkStackNode *oldTop = top;*outData = oldTop->data;// 新栈顶为原栈顶的下一节点top = top->next;// 释放原栈顶节点free(oldTop);oldTop = NULL;return top;
}

取栈顶元素

bool LinkStack_GetTop(LinkStackNode *top, DataType_t *outData) {if (LinkStack_IsEmpty(top)) {printf("Stack is empty! GetTop failed.\n");return false;}*outData = top->data;return true;
}

遍历(从栈顶到栈底)

void LinkStack_Print(LinkStackNode *top) {if (LinkStack_IsEmpty(top)) {printf("Stack is empty!\n");return;}LinkStackNode *p = top;  // 辅助指针printf("Stack Elements (Top -> Bottom): ");while (p != NULL) {printf("%d ", p->data);p = p->next;}printf("\n");
}

销毁

LinkStackNode *LinkStack_Destroy(LinkStackNode *top) {LinkStackNode *p = top;while (p != NULL) {LinkStackNode *temp = p;  // 保存当前节点p = p->next;              // 移动到下一节点free(temp);               // 释放当前节点temp = NULL;}return NULL;  // 销毁后栈顶为NULL
}

顺序栈与链式栈的对比

对比维度	顺序栈（数组）	链式栈（单链表）
存储方式	连续内存空间（数组）	不连续内存空间（节点动态分配）
空间效率	可能浪费空间（数组容量固定，未用满）	无空间浪费（按需分配节点）
时间效率	入栈 / 出栈 O (1)，扩容 O (n)（可选）	入栈 / 出栈 O (1)（头插 / 头删）
判满需求	必须判满（数组容量固定）	无需判满（动态扩展）
实现复杂度	较简单（数组操作）	较复杂（节点指针管理，需避免内存泄漏）
适用场景	已知数据规模、需高效存取的场景	数据规模不确定、需灵活扩展的场景

栈的典型应用

应用 1：十进制转十六进制（处理 0 值）

核心逻辑
- 原理：十进制数反复除以 16，余数作为十六进制位（逆序排列，需用栈存储余数，最后出栈即正序）。
- 补充：若输入为 0，需单独处理（原 do-while 循环不执行，需手动入栈 '0'）。

代码

void SeqStack_Dec2Hex(SeqStack_t *Manager, unsigned int Data) {// 处理Data=0的情况（否则do-while不执行，栈为空）if (Data == 0) {SeqStack_Push(Manager, '0');} else {int remainder;do {remainder = Data % 16;// 余数映射：0-9→'0'-'9'，10-15→'A'-'F'if (remainder < 10) {SeqStack_Push(Manager, remainder + '0');} else {SeqStack_Push(Manager, remainder - 10 + 'A');}Data /= 16;} while (Data != 0);}// 出栈输出（栈中为逆序，出栈后为正序）printf("Hex Result: 0x");while (!SeqStack_IsEmpty(Manager)) {printf("%c", (char)SeqStack_Pop(Manager));}printf("\n");
}// 测试：输入0→0x0；输入255→0xFF；输入10→0xA

应用 2：有效括号判断（支持多类型括号）

核心逻辑
- 需求：判断字符串中()、[]、{}是否配对（左括号入栈，右括号与栈顶匹配，最后栈需为空）。
- 补充：原笔记仅处理()，此处扩展多类型括号，且增加 “右括号无匹配左括号”“左括号未闭合” 的判断。

代码

// 有效括号判断（支持()、[]、{}）
bool SeqStack_IsValidBracket(SeqStack_t *Manager, const char *str) {if (str == NULL) return false;  // 空字符串无效const char *p = str;while (*p != '\0') {// 左括号：入栈if (*p == '(' || *p == '[' || *p == '{') {SeqStack_Push(Manager, *p);}// 右括号：判断匹配else if (*p == ')' || *p == ']' || *p == '}') {// 若栈空，右括号无匹配左括号→无效if (SeqStack_IsEmpty(Manager)) {return false;}// 取出栈顶左括号，判断是否匹配char topBracket = (char)SeqStack_Pop(Manager);if ((*p == ')' && topBracket != '(') ||(*p == ']' && topBracket != '[') ||(*p == '}' && topBracket != '{')) {return false;  // 类型不匹配}}// 非括号字符：忽略（若需求为“仅括号”，可返回false）p++;}// 遍历结束后，栈需为空（所有左括号均闭合）return SeqStack_IsEmpty(Manager);
}// 测试："()[]{}"→true；"([)]"→false；"({})"→true；"("→false

其他应用场景

函数调用栈：C 语言中，函数调用时会创建 “栈帧”（存储返回地址、局部变量、寄存器值），函数执行完后栈帧出栈，回到调用处（遵循 LIFO）。
表达式求值：将中缀表达式（如3+4*2）转为后缀表达式（3 4 2 * +），用栈处理运算符优先级，再通过栈计算后缀表达式结果。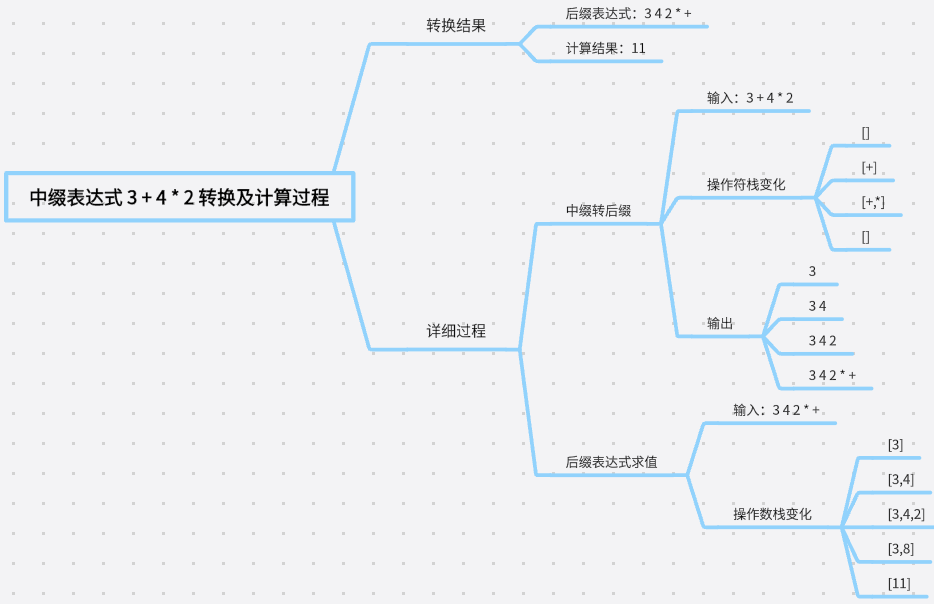

函数代码

// 中缀表达式转后缀表达式
void infixToPostfix(char* infix, char* postfix) {int i, j;Stack* stack = createStack(strlen(infix));for (i = 0, j = 0; infix[i]; ++i) {// 如果是操作数，直接添加到后缀表达式if (isdigit(infix[i]) || infix[i] == '.') {postfix[j++] = infix[i];}// 如果是左括号，入栈else if (infix[i] == '(') {pushOperator(stack, infix[i]);}// 如果是右括号，弹出所有运算符直到遇到左括号else if (infix[i] == ')') {while (!isEmpty(stack) && peekOperator(stack) != '(') {postfix[j++] = ' ';  // 用空格分隔不同的元素postfix[j++] = popOperator(stack);}popOperator(stack);  // 弹出左括号，不加入后缀表达式}// 如果是运算符else if (isOperator(infix[i])) {postfix[j++] = ' ';  // 用空格分隔不同的元素// 弹出所有优先级大于等于当前运算符的运算符while (!isEmpty(stack) && precedence(peekOperator(stack)) >= precedence(infix[i])) {postfix[j++] = popOperator(stack);postfix[j++] = ' ';}pushOperator(stack, infix[i]);}}// 弹出栈中剩余的所有运算符while (!isEmpty(stack)) {postfix[j++] = ' ';postfix[j++] = popOperator(stack);}postfix[j] = '\0';free(stack->operatorItems);free(stack->numberItems);free(stack);
}// 计算后缀表达式
double evaluatePostfix(char* postfix) {Stack* stack = createStack(strlen(postfix));double num = 0, decimal = 0, decimalPlace = 0;int i;for (i = 0; postfix[i]; ++i) {// 如果是数字或小数点，解析为数字if (isdigit(postfix[i]) || postfix[i] == '.') {if (postfix[i] == '.') {decimal = 1;decimalPlace = 1;continue;}if (decimal) {num += (postfix[i] - '0') / pow(10, decimalPlace);decimalPlace++;} else {num = num * 10 + (postfix[i] - '0');}}// 如果是空格且之前有数字，将数字入栈else if (postfix[i] == ' ' && (isdigit(postfix[i-1]) || postfix[i-1] == '.')) {pushNumber(stack, num);num = 0;decimal = 0;}// 如果是运算符，弹出两个数字进行运算else if (isOperator(postfix[i])) {double val1 = popNumber(stack);double val2 = popNumber(stack);double result;switch (postfix[i]) {case '+':result = val2 + val1;break;case '-':result = val2 - val1;break;case '*':result = val2 * val1;break;case '/':if (val1 == 0) {printf("错误：除数不能为零！\n");return NAN;}result = val2 / val1;break;case '^':result = pow(val2, val1);break;default:result = 0;}pushNumber(stack, result);}}double finalResult = popNumber(stack);free(stack->operatorItems);free(stack->numberItems);free(stack);return finalResult;
}