0. 前置知识
给定集合 \(S\) 和运算 \(\circ\),若 \(\circ\) 对 \(S\) 封闭,且有单位元(\(a \circ e = a\))、逆元(\(a \circ a^{-1} = e\))、结合律、交换律,则称 \(S\) 对 \(\circ\) 构成 Abelian 群。
一个大人遇到了一个小孩。
大人:你知道 \(7 + 5\) 等于多少吗?
小孩:不知道。
大人:那你知道 \(5 + 7\) 等于多少吗?
小孩:不知道。
大人:那你知道什么?
小孩:我知道 \(7 + 5 = 5 + 7\),因为 \(\Z\) 对 \(+\) 构成 Abelian 群。
1. 椭圆曲线(EC)
1.1 定义
我们定义满足 Weierstrass 方程(\(y^2 = x^3 + ax + b\))的点集为椭圆曲线。下面是 \(a = -2, b = 5\) 时的图像。
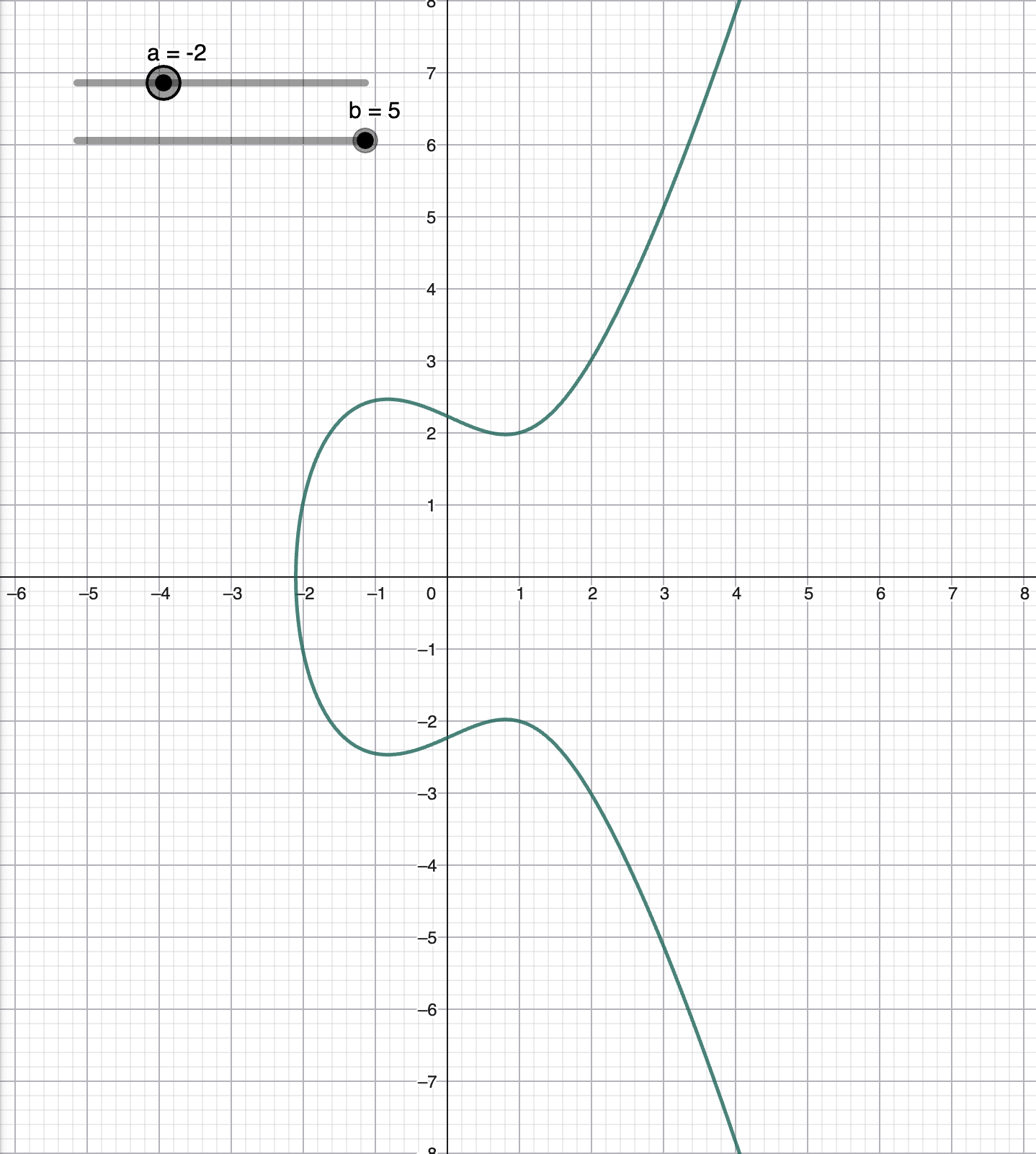
容易发现图像关于 \(x\) 轴对称。
计算机计算浮点数的效率不高,所以计算时一般使用同余形式:
其中 \(p\) 是一个大质数。
一般会额外定义一个无穷远点 \(\mathcal{O}\),规定 \(\mathcal{O}\) 也属于椭圆曲线。
注:此处的无穷远点需要从射影几何的角度去理解,但笔者不会射影几何。
早知道之前就学一下了。
1.2 点的加法
现有椭圆曲线 \(E : y^2 = x^3 + ax + b\),对于两点 \(P, Q \in E\) 定义:
- \(P \neq Q\) 时:设 \(PQ\) 交 \(E\) 于 \(R\),\(P + Q\) 为 \(R\) 关于 \(x\) 轴的对称点。
- \(P = Q\) 时:作 \(E\) 在 \(P\) 上的切线 \(l\),设 \(l\) 交 \(E\) 于 \(R\),\(P + Q\) 为 \(R\) 关于 \(x\) 轴的对称点。
- \(P\) 与 \(Q\) 关于 \(x\) 轴对称时:\(P + Q = \mathcal{O}\),\(Q = -P\)。
- \(P + \mathcal{O} = \mathcal{O} + P = P\)。
容易发现,\(P + Q \in E\),且 \(+\) 满足交换律。\((E, +)\) 构成 Abelian 群:
- 单位元:\(\mathcal{O}\)。
- 逆元:\(P\) 的逆元为 \(P\) 关于 \(x\) 轴的对称点。
- 结合律:证明需要射影几何知识,或暴算。
- 交换律:显然满足。
我们来进行一些计算。设 \(P = (x_1, y_1), Q = (x_2, y_2), R = P + Q = (x_3, y_3)\),我们考虑求出 \(x_3, y_3\)。下设 \(P \neq \mathcal{O}, Q \neq \mathcal{O}, R \neq \mathcal{O}\)。
经过计算可知,设:
则:
如果你考虑了可行性,会发现 \(P = Q\) 时切线可能不唯一,我们要避免这种情况的发生。那么考虑求出这种情况的充要条件。
从特殊到一般。发现切线不唯一有至少两种情况:尖点或相交。
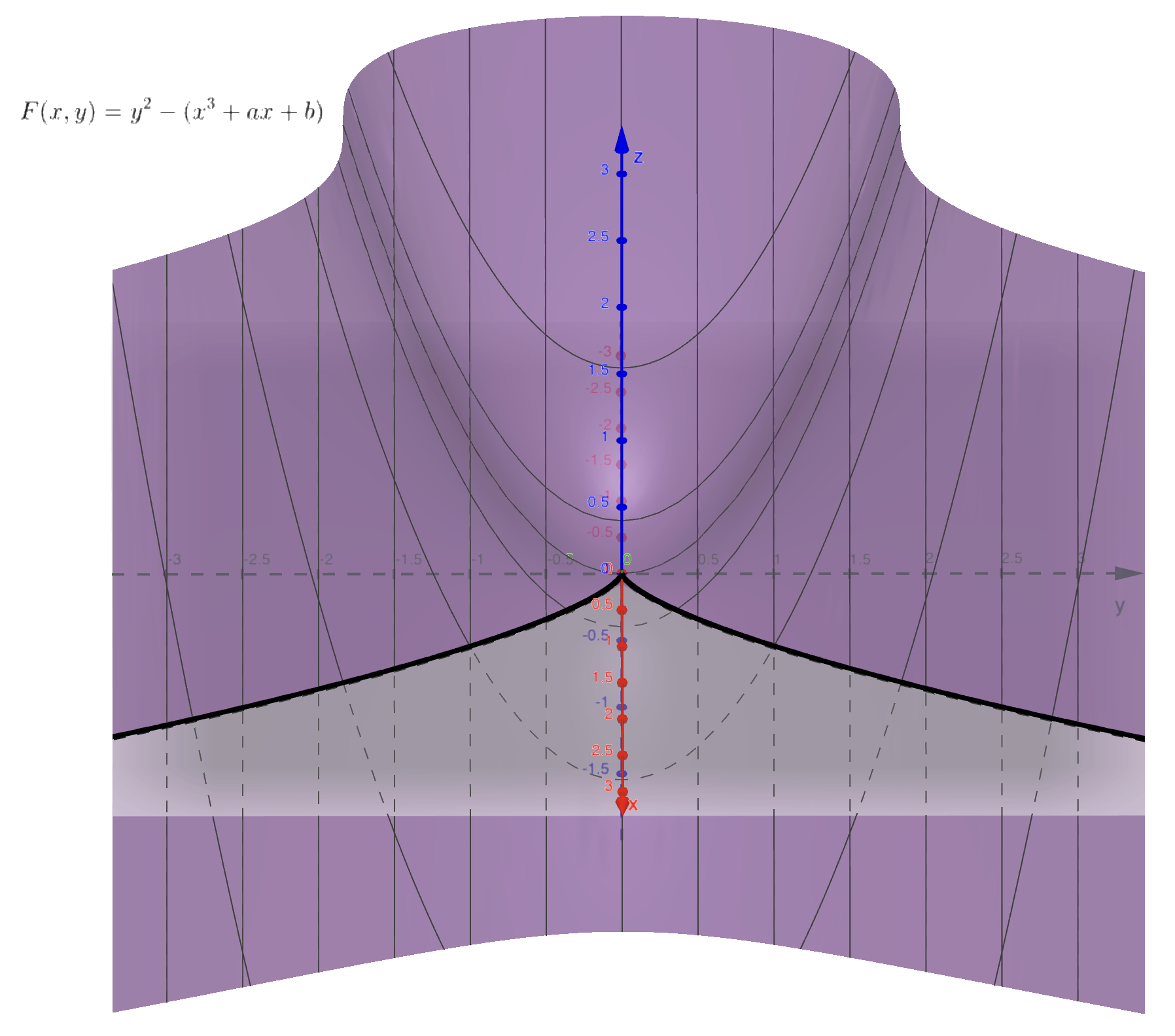

图中 \(F\) 与 \(z = 0\) 的交线为椭圆曲线。猜猜为什么要这样画图。
以尖点的情况举例,我们考虑 \(\dfrac{\partial F}{\partial x}\) 和 \(\dfrac{\partial F}{\partial y}\)。

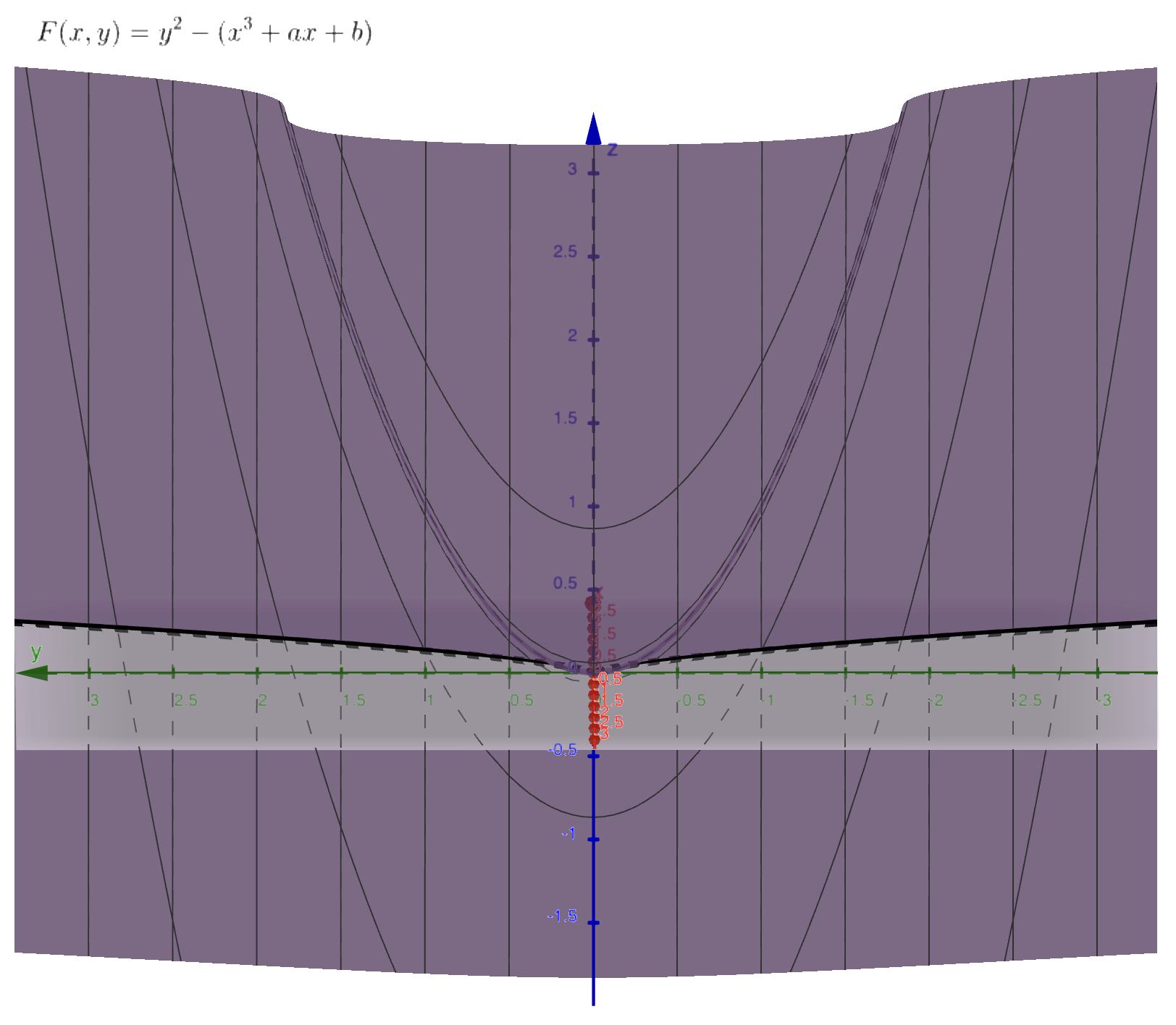
猜猜 \(a, b\) 的值。
观察到尖点满足 \(F = \dfrac{\partial F}{\partial x} = \dfrac{\partial F}{\partial y} = 0\)。可以证明,这是充要条件。但我不会证。
算出来 \(\dfrac{\partial F}{\partial x}\) 和 \(\dfrac{\partial F}{\partial y}\):
则 \(x = \dfrac{\sqrt{-3a}}{3}, y = 0\)。代入 \(E\):
两边平方得:
即:
所以这种情况发生的充要条件就是 \((1)\) 式。
1.3 点的数乘
现有椭圆曲线 \(E : y^2 = x^3 + ax + b\) 与点 \(P\),定义 \(kP = \underbrace{P + P + \cdots + P}_k\),其中 \(k \in \N\)。
如何快速计算 \(kP\)?考虑快速幂,因为:
所以可以 \(O(\log k)\) 递推计算。
发现当 \(kP = \mathcal{O}\) 时比较特殊。对于点 \(P\),定义 \(P\) 的阶为最小的正整数 \(k\) 满足 \(kP = \mathcal{O}\)。
2. 椭圆曲线离散对数问题(ECDLP)
题目:给定点 \(P, Q\),考虑求解 \(k\) 满足 \(Q = kP\)。
因为每次加法 \(x\) 坐标的指数都会乘 \(2\),所以这实际上是在求解离散对数问题。
不幸的是,离散对数问题仍不存在多项式时间的算法。常用的算法为 BSGS 算法,但时间复杂度为 \(O \left( \sqrt{m} \right)\),其中 \(m\) 为模数。一般情况下 \(m \ge 2^{128}\),所以 BSGS 算法运行时间是不现实的。基于这一点,人们设计出了许多加密算法,如 RSA。
3. Diffie-Hellman 算法
用途
一般被用于密钥协商。
流程
- Alice 和 Bob 使用同一个椭圆曲线 \(E\) 和基点 \(G\)(阶为大质数 \(q\))。
- Alice 随机生成私钥 \(d_A\),计算公钥 \(Q_A = d_A G\)。Bob 随机生成私钥 \(d_B\),计算公钥 \(Q_B = d_B G\)。
- Alice 向 Bob 发送 \(Q_A\),Bob 向 Alice 发送 \(Q_B\)。
- Alice 计算出共同密钥 \(S = d_A Q_B\),Bob 计算出共同密钥 \(S = d_B Q_A\)。
注意到 \(d_A Q_B = d_B Q_A = d_A d_B G\),所以两人获得了同一个密钥。
4. ElGamal 算法
用途
用于加密 / 解密消息。
流程
- Alice 和 Bob 使用同一个椭圆曲线 \(E\) 和基点 \(G\)(阶为大质数 \(q\))。
- Bob 随机生成私钥 \(d \in (1, q)\),并计算公钥 \(Q = dG\)。
加密
假设 Alice 要发送消息 \(M\) 给 Bob。
- 把 \(M\) 变换到 \(E\) 上,设变换后为 \(M'\)。
- 选择随机整数 \(k \in (1, q)\)。
- 计算 \((C_1, C_2) = (kG, M' + kQ)\)。
- 发送 \((C_1, C_2)\) 给 Bob。
解密
- 计算 \(M' = C_2 - kQ = C_2 - kdG = C_2 - dC_1\)。
- 通过 \(M'\) 变换回 \(M\)。
攻击方法
发现对于不同的 \(k\),计算 \(kQ\)(或其他数乘)的时间是不同的,所以理论上可以测量计算 \(kQ\) 的时间(或其他信息)来获知 \(k\)。CTF 对于上述攻击方法出了一道题,当然我是不会做的。
