完备归纳法需要画出真值表,这里省略,直接列出每一个检验的式子
(T2)\(X + 1 = 1\)
- 当\(X = 0\)时:\(0 + 1 = 1\)(成立)
- 当\(X = 1\)时:\(1 + 1 = 1\)(成立)
因此,\(X + 1 = 1\)得证。
(T2D)\(X \cdot 0 = 0\)
- 当\(X = 0\)时:\(0 \cdot 0 = 0\)(成立)
- 当\(X = 1\)时:\(1 \cdot 0 = 0\)(成立)
因此,\(X \cdot 0 = 0\)得证。
(T3)\(X + X = X\)
- 当\(X = 0\)时:\(0 + 0 = 0\)(成立)
- 当\(X = 1\)时:\(1 + 1 = 1\)(成立)
因此,\(X + X = X\)得证。
(T3D)\(X \cdot X = X\)
- 当\(X = 0\)时:\(0 \cdot 0 = 0\)(成立)
- 当\(X = 1\)时:\(1 \cdot 1 = 1\)(成立)
因此,\(X \cdot X = X\)得证。
(T4)\(\overline{\overline{X}} = X\)
- 当\(X = 0\)时:\(\overline{\overline{0}} = \overline{1} = 0\)(等于\(X = 0\))
- 当\(X = 1\)时:\(\overline{\overline{1}} = \overline{0} = 1\)(等于\(X = 1\))
因此,\(\overline{\overline{X}} = X\)得证。
(T5)\(X + \bar{X} = 1\)
- 当\(X = 0\)时:\(0 + \bar{0} = 0 + 1 = 1\)(成立)
- 当\(X = 1\)时:\(1 + \bar{1} = 1 + 0 = 1\)(成立)
因此,\(X + \bar{X} = 1\)得证。
(T5D)\(X \cdot \bar{X} = 0\)
- 当\(X = 0\)时:\(0 \cdot \bar{0} = 0 \cdot 1 = 0\)(成立)
- 当\(X = 1\)时:\(1 \cdot \bar{1} = 1 \cdot 0 = 0\)(成立)
因此,\(X \cdot \bar{X} = 0\)得证。
德·摩根定理指出,对于逻辑表达式\(A + B\)的反是\(\bar{A} \cdot \bar{B}\),对于\(A \cdot B\)的反是\(\bar{A} + \bar{B}\)
给定表达式\(X + Y \cdot Z\),其正确取反应为\(\bar{X} \cdot (\bar{Y} + \bar{Z})\),而非题目所称的\(X \cdot Y + Z\)
(5)
| W | X | Y | Z | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
(6)
| A | B | C | D | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
(1).
标准与-或:
首先,将每个最小项展开为变量的乘积形式:
- \(m_2 = \bar{A} B \bar{C}\)(二进制 010)
- \(m_4 = A \bar{B} \bar{C}\)(二进制 100)
- \(m_6 = A B \bar{C}\)(二进制 110)
- \(m_7 = A B C\)(二进制 111)
因此,\(F = \bar{A} B \bar{C} + A \bar{B} \bar{C} + A B \bar{C} + A B C\)
标准或-与:
确定 F=0 的最小项:总共 8 个最小项(0 到 7),给定的是 2、4、6、7,因此缺失的是 0、1、3、5。
这些对应最大项\(M_0, M_1, M_3, M_5\)。
将每个最大项展开为变量的加法形式:
- \(M_0\)(000):\(A + B + C\)
- \(M_1\)(001):\(A + B + \bar{C}\)
- \(M_3\)(011):\(A + \bar{B} + \bar{C}\)
- \(M_5\)(101):\(\bar{A} + B + \bar{C}\)
因此,\(F = (A + B + C)(A + B + \bar{C})(A + \bar{B} + \bar{C})(\bar{A} + B + \bar{C})\)
(6)
标准与-或:
首先,将表达式展开为最小项之和:
- \(A = A(\bar{B} \bar{C} + \bar{B} C + B \bar{C} + B C) = A \bar{B} \bar{C} + A \bar{B} C + A B \bar{C} + A B C\)(对应\(m_4, m_5, m_6, m_7\))
- \(\bar{A} B = \bar{A} B (\bar{C} + C) = \bar{A} B \bar{C} + \bar{A} B C\)(对应\(m_2, m_3\))
- \(B C = B C (A + \bar{A}) = A B C + \bar{A} B C\)(对应\(m_7, m_3\))
合并(重复项如\(m_3, m_7\)只取一次),得到最小项:2、3、4、5、6、7。
展开为:\(F = \bar{A} B \bar{C} + \bar{A} B C + A \bar{B} \bar{C} + A \bar{B} C + A B \bar{C} + A B C\)
标准或-与:
从展开的最小项确定 F=0 的位置:缺失 0、1(即 000 和 001)。
这些对应最大项\(M_0, M_1\):
- \(M_0\):\(A + B + C\)
- \(M_1\):\(A + B + \bar{C}\)
因此,\(F = (A + B + C)(A + B + \bar{C})\)
2输入与非门能够构成逻辑门的完备集,可以通过显示如何仅用 NAND 门构建 NOT、AND 和 OR 来证明
-
构建 NOT 门:
- 输入:A
- 电路:将 A 连接到 NAND 门的两个输入。
- 输出:A NAND A = NOT(A)
-
构建 AND 门:
- 输入:A, B
- 电路:先计算 A NAND B,然后将结果输入到一个 NOT 门(用 NAND 实现)。
- 但由于 NOT 是 (X NAND X),所以 AND(A, B) = NOT(A NAND B) = (A NAND B) NAND (A NAND B)
-
构建 OR 门:
- 输入:A, B
- 电路:OR(A, B) = NOT(NOT(A) AND NOT(B)),用德摩根定律。
- 用 NAND 实现:NOT(A) = A NAND A
NOT(B) = B NAND B
然后 NOT(A) AND NOT(B) = ( (A NAND A) NAND (B NAND B) ) NAND ( (A NAND A) NAND (B NAND B) )
最后 OR = NOT(上述结果) = 上述结果 NAND 自身
-
扩展到任意函数:
- 既然能构建 {AND, OR, NOT},就可以实现任何布尔函数(例如,通过最小项之和)。
- 对于多输入门:如 3 输入 NAND 可以用两个 2 输入 NAND 级联(先两个输入 NAND,结果与第三个输入 NAND)。
这个证明显示 NAND 是通用门,因此是完备的。
2输入异或门不能构成逻辑门的完备集
(2)
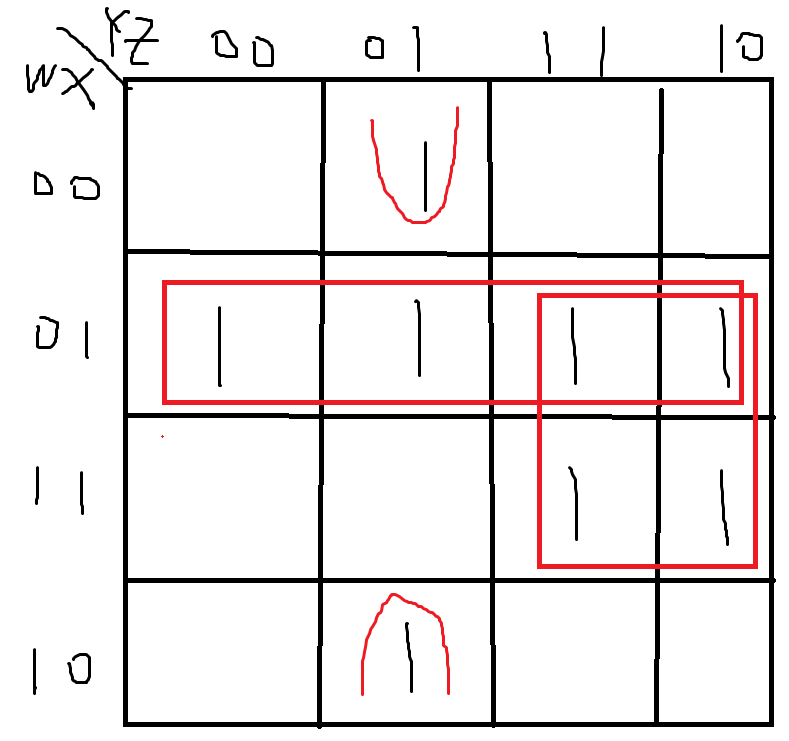
画出的卡诺图如上,于是可以得到答案为\(\bar{W} ⋅ X + X ⋅ Y + \bar{X} ⋅ \bar{Y} ⋅ Z\)
利用12题的技巧,转换为与非-与非表达式为[ (X NAND Y) NAND ( ~W NAND X ) NAND ( ~X NAND ~Y NAND Z ) ]
(5)
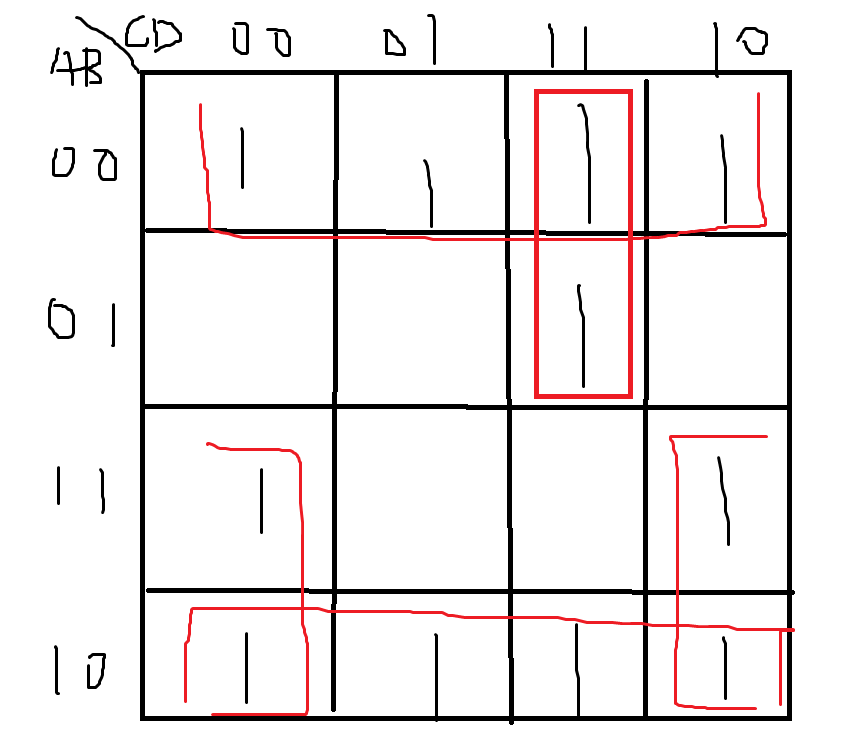
卡诺图如上,于是可以得到答案为\(\bar{B}+\bar{A}CD+A\bar{D}\)
转换为与非-与非表达式为\(\overline{ \overline{\bar{B} \cdot \bar{B}} \cdot \overline{\bar{A} \cdot C \cdot D} \cdot \overline{A \cdot \bar{D}} }\)
