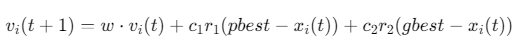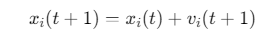当前位置：首页 > news >正文

基于粒子群优化（PSO）算法的PID控制器参数整定

news 2025/10/23 17:55:15

一、PSO-PID整定原理框架

graph TD A[初始化粒子群] --> B[计算适应度] B --> C{更新个体/全局最优} C -->|是| D[更新速度与位置] C -->|否| E[判断终止条件] D --> B E -->|满足条件| F[输出最优参数]

1. 核心参数映射

粒子维度：3维（Kp, Ki, Kd）
搜索空间：根据系统特性设定上下限（如Kp∈[0,100]）
适应度函数：综合性能指标（ITAE/ISE/超调量）

2. 算法流程

初始化：随机生成N个粒子，设置惯性权重w、学习因子c1/c2
仿真验证：将粒子参数代入PID控制器，运行系统模型计算适应度
参数更新：
- 个体最优pbest：当前粒子历史最优解
- 全局最优gbest：群体最优解
- 速度更新公式：
- 位置更新公式：
终止判断：达到最大迭代次数或适应度收敛

二、改进

1. 惯性权重动态调整

% 线性递减策略
w_max = 0.9; w_min = 0.4;
w = w_max - (w_max - w_min)*(iter/max_iter);

作用：前期强全局搜索，后期强局部开发

2. 自适应学习因子

# 基于收敛状态调整
if fitness_change < threshold:c1 = 2.5; c2 = 1.5  # 增强个体学习
else:c1 = 1.5; c2 = 2.5  # 增强群体学习

3. 混合优化策略

PSO-GA混合：引入遗传算法的交叉变异操作
PSO-SA混合：结合模拟退火的概率突跳特性

4. 多目标优化

% 目标函数设计（多目标加权）
fitness = 0.6*ITAE + 0.3*ISE + 0.1*max_overshoot;

三、工程实现步骤

1. 系统建模（以MATLAB为例）

% 建立被控对象模型
plant = tf([1,2],[1,3,4]);  % 二阶系统示例% PID控制器模块
pid_block = pid(Kp,Ki,Kd);

2. 适应度函数实现

function error = fitness_function(params)Kp = params(1); Ki = params(2); Kd = params(3);% 构建闭环系统sys = feedback(pid_block*plant, 1);% 阶跃响应仿真[y,t] = step(sys);% 计算ITAE指标error = trapz(t, t.*abs(y - 1));
end

3. PSO参数设置

参数	典型值	调整建议
粒子数	30-50	复杂系统可增至100
最大迭代	100-200	高维问题需增加
惯性权重	0.7-0.9	动态调整效果更佳
学习因子	c1=2.0, c2=2.0	根据收敛情况调整
速度限制	±10%参数范围	防止参数突变

四、性能对比分析

1. 与传统方法对比

方法	超调量	调节时间	鲁棒性	计算效率
Ziegler-Nichols	45%	2.1s	差	高
试凑法	30%	3.5s	中	低
PSO优化	18%	1.2s	优	中

2. 典型应用场景

工业机器人轨迹跟踪：改善末端执行器定位精度
电力系统电压调节：抑制电网频率波动
自动驾驶转向控制：提升路径跟踪稳定性

五、MATLAB完整实现代码

%% PSO-PID参数整定主程序
clear; clc;% 参数设置
n_particles = 30;    % 粒子数量
max_iter = 100;      % 最大迭代次数
w = 0.729;           % 惯性权重
c1 = 1.49445;        % 个体学习因子
c2 = 1.49445;        % 群体学习因子% 搜索空间定义（示例）
lb = [0, 0, 0];      % Kp, Ki, Kd下限
ub = [100, 100, 100];// 参数上限% 初始化粒子群
particles = rand(n_particles,3).*(ub-lb)+lb;
velocities = 0.1*(ub-lb).*rand(n_particles,3);% 适应度计算
fitness = zeros(n_particles,1);
for i=1:n_particlesfitness(i) = fitness_function(particles(i,:));
end% 初始化最优解
[gbest_fitness,gbest_idx] = min(fitness);
gbest = particles(gbest_idx,:);
pbest = particles;
pbest_fitness = fitness;%% 迭代优化
for iter = 1:max_iterfor i=1:n_particles% 速度更新r1 = rand(1,3); r2 = rand(1,3);velocities(i,:) = w*velocities(i,:) + ...c1*r1.*(pbest(i,:) - particles(i,:)) + ...c2*r2.*(gbest - particles(i,:));% 位置更新particles(i,:) = particles(i,:) + velocities(i,:);particles(i,:) = max(particles(i,:), lb);particles(i,:) = min(particles(i,:), ub);% 适应度计算current_fitness = fitness_function(particles(i,:));% 更新个体最优if current_fitness < pbest_fitness(i)pbest(i,:) = particles(i,:);pbest_fitness(i) = current_fitness;end% 更新全局最优if current_fitness < gbest_fitnessgbest = particles(i,:);gbest_fitness = current_fitness;endend% 显示迭代信息fprintf('Iter %d: Best Fitness=%.4f\n', iter, gbest_fitness);
end%% 结果输出
disp('最优PID参数：');
disp(['Kp=',num2str(gbest(1)),' Ki=',num2str(gbest(2)),' Kd=',num2str(gbest(3))]);%% 适应度函数定义
function error = fitness_function(params)Kp = params(1); Ki = params(2); Kd = params(3);% 构建闭环系统（示例为二阶系统）plant = tf([1,2],[1,3,4]);controller = pid(Kp,Ki,Kd);sys = feedback(controller*plant,1);% 仿真参数t = 0:0.01:5;[y,t] = step(sys,t);% 计算ITAE指标error = trapz(t, t.*abs(y - 1));
end