感觉这题真的不止黄(可能是我太菜了<(_ _)>
这道题会让我们联想到数位dp(其实没有多少关系(@_@)
这里还是借用的老师的思路
计算l-r之间有趣数字的个数,也就是0-r之间有趣数字的个数减去0-(l-1)之间有趣数字的个数
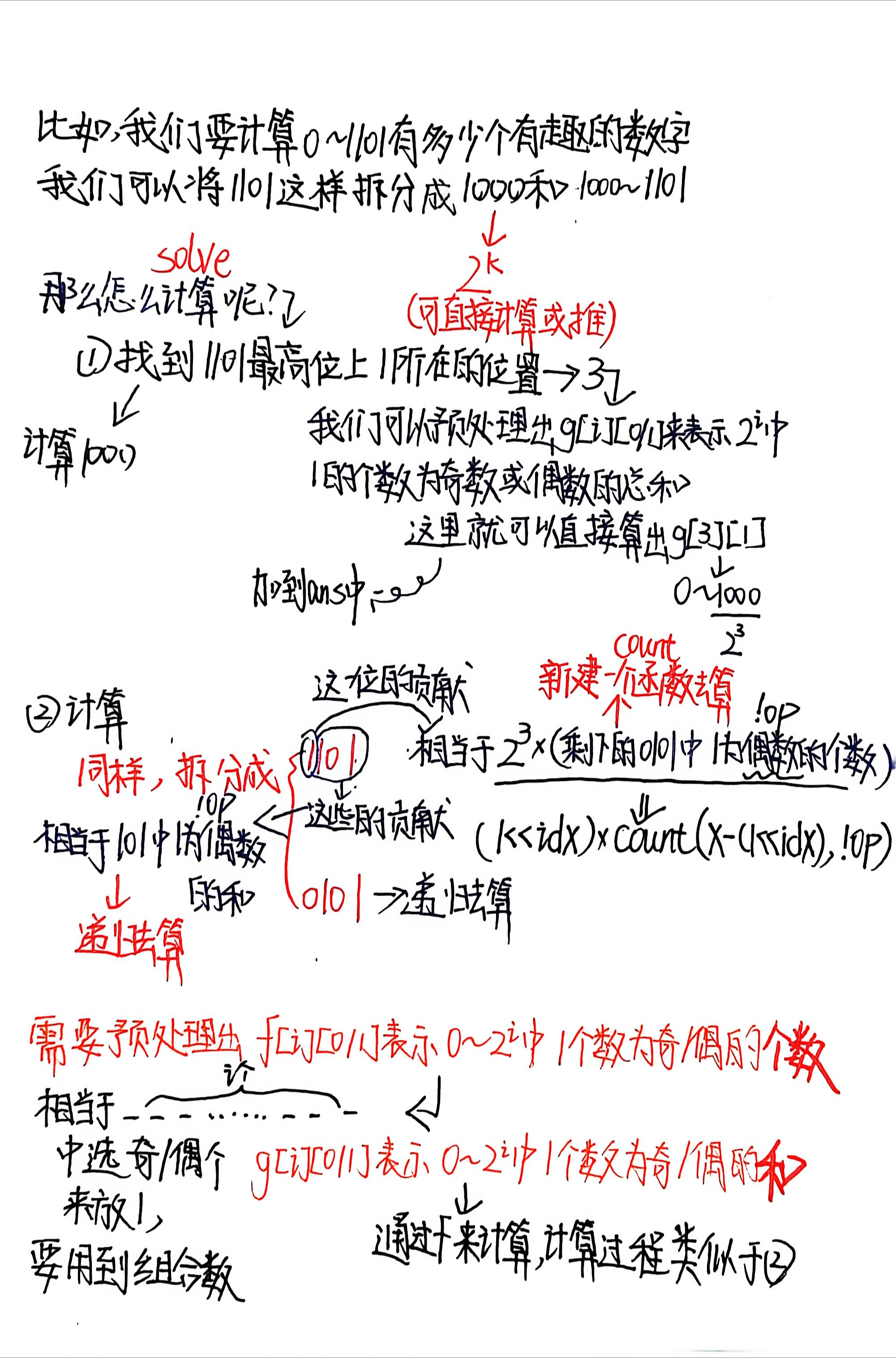
我们想想怎么计算从0~x之间一共有多少个有趣数字
另外 30% 的测试点,保证 l=1 并且 r=2^k −1,其中 k 是大于 1 的正整数。
题目中的这个有提示意义的数据告诉我们,2^k-1可以直接计算(或推出来), 这样我们就可以试着将数拆成类似于2^k-1的形式
like this
代码放上,如果有什么问题记得@我
https://www.luogu.com.cn/discuss/1165743
还有我关于这道题有些问题,希望大佬解答QWQ
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=31;
int l,r;
LL f[N][2],g[N][2],c[N][N];void init(){for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(j)c[i][j]=c[i-1][j-1]+c[i-1][j];else c[i][j]=1;f[i][j&1]+=c[i][j];}}for(int i=0;i<N;i++){g[i][0]=f[i-1][1]*(1<<(i-1))+g[i-1][0]+g[i-1][1];g[i][1]=f[i-1][0]*(1<<(i-1))+g[i-1][1]+g[i-1][0];}
}LL count(int x,int op){if(x==0){return f[x][op];}int idx=0;for(int i=30;i>=0;i--){if((x>>i)&1){idx=i;break;} } LL p=(1<<idx);return f[idx][op]+count(x-p,op^1);
}LL solve(int x,int op){
// cout<<x<<"\n";LL res=0;int idx=-1;for(int i=30;i>=0;i--){if((x>>i)&1){idx=i;break;} } if(idx==-1){return 0;}LL p=(1<<idx);res=g[idx][op]+p*count(x-p,op^1)+solve(x-p,op^1);return res;
}int main(){init();cin>>l>>r;cout<<solve(r,1)-solve(l-1,1);//1 奇数 0 偶数 return 0;
}

