学期2023-2024-1 学号20252332 《网络》第二周自学总结“密码学基础”
1.简单密码闲谈
2.密码学部分相关数学基础了解
3.国产密钥基本概念掌握
4.实验
简单密码闲谈
0.历史渊源,从原始天性狩猎,到古代岩画信息记录,再到古文字,比如楔形文字等等,如何对文字中的信息解密?现代人类无论何种文化,都有相当成熟的语言体系,对于古文字,古代文化,也许我们有一天能利用科技解密那些奇妙的符号。
1.隐写笔或许是当下一种有趣的文具,早在公元1世纪,古罗马人就利用大戟科植物风干后透明,加热后变棕色,发明隐写墨水。洋葱,柠檬水也可以制作隐写墨水。这些是成本较低的制作方法。其他现代化学方法多样,不再过多阐述。
2.斯巴达密码棒,达·芬奇密码筒,经典的物理密码设计,在一些影视或小说中会见到这些物件,一些有趣的风味。
3.古典密码,现代密码的前身:代换密码,置换密码,弗纳姆密码......一些基础解密训练中也许会用到这些数学原理进行解密,多应用于文本。
4.机械密码,ENIGMA密码机笔者第一次见是在《模仿游戏》电影中见到,数学基础未完全掌握,原理看不懂,但不影响欣赏电影的精彩。其他机械密码不过多阐述。
密码学部分相关数学基础
1.整数分解。任意一个大于1的自然数N,如果N不为素数,那么 N可以被唯一分解成有限个素数的乘积。RSA依赖于大整数分解。
2.模运算。用a mod n表示余数r。a≡r(mod n)。逆元。任意的x,存在y,使得x*y/x+y=1 mod n,x,y互为乘法逆元,加法逆元。(模指数运算略)
3.有限域。群,域,环,均是代数结构。 
3。欧几里得算法。求最大公因子:
- 设a、b是两个任意正整数,它们的最大公因子记为gcd(a,b),简记为(a ,b),则(a,b)=(b,a mod b)。
- 如(77,33)=(33,77 mod 33)=(33,11)=(11,0)=11。
求乘法逆元:举例求5在模17下的乘法逆元 - gcd(17.5):17=53+2,5=22+1,2=1*2+0
- 运用递推公式:初始值t0=0,t1=1,代入递推公式。0-31=-3,1-2(-3)=7
- 验证5*7≡1(mod 17),所以5,7互为乘法逆元。
4.CRT,跟gcd差不了多少,略
5.椭圆曲线,学的有限,略
6.公钥密码的安全性基于数学难题,比如: - RSA 基于大整数分解困难性(把一个极大的数分解成两个素数很难)
- ElGamal 基于离散对数困难性(反向计算指数很难)
- ECC 基于椭圆曲线离散对数困难性(更短的密钥就能达到和 RSA 同样的安全强度)
密码基本概念掌握
1. 核心概念
- 分组密码:按“块”加密数据(如AES),是文件、硬盘加密的基础。
- 公钥密码:用“公钥(加密)+私钥(解密)”配对,解决“密钥怎么安全传给对方”的问题(网安里的登录、支付都靠它)。
- 对称密码 1把钥匙(加密=解密),快;代表:AES(常用)、SM4(国密)用在文件/硬盘/WiFi加密
- 非对称密码(公钥密码) 2把钥匙(公钥加密、私钥解密),慢;代表:RSA(经典)、ECC(轻量)、SM2(国密)用在登录认证、支付签名
- 关键算法
AES 对称密码“顶流”,安全强度高,网安中几乎必用(替代老的DES)
RSA 非对称密码“入门款”,理解其“公钥传、私钥存”逻辑即可,不用深算数学
ECC 非对称密码“新主流”,密钥短、省资源,手机/物联网常用
国密算法(SM系列) 国内合规必学:SM4(对称)、SM2(非对称)、SM3(哈希);政务/金融项目要用到
2.核心逻辑
密码学的安全不是“绝对安全”,而是“基于数学难题的相对安全”(比如RSA靠大整数分解难,ECC靠椭圆曲线离散对数难)——这是网安里“攻防思维”的基础。
实验
实验要求:实践OpenSSL命令,至少会用sm2加密解密、签名验签,会用sm3计算字符串或文件的Hash值,会用sm4算法算法对字符串或者文件进行加密解密,提交实践过程文档,不少于10张截图。
参考(https://www.cnblogs.com/rocedu/p/14891816.html)#opensslgmssl-tassl
已完成,附录pdf【20252332国密sm234】
检查配件
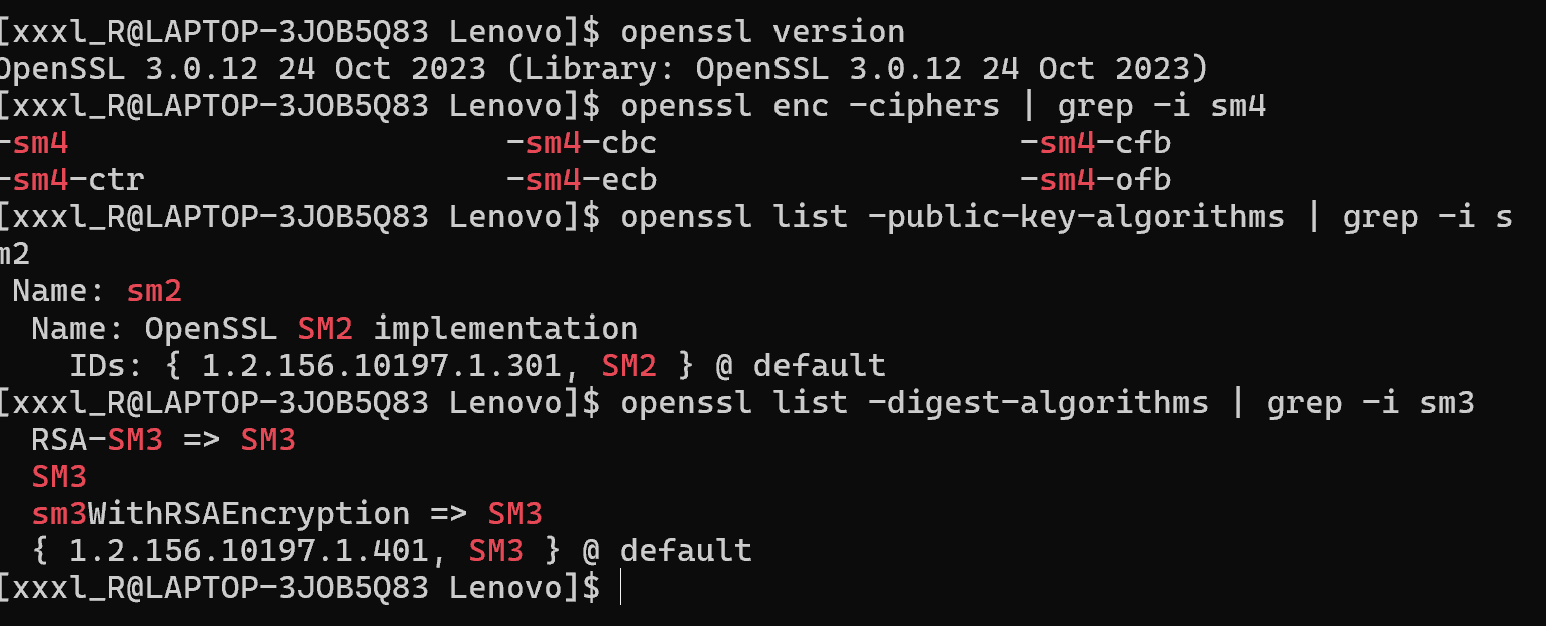
sm3文本文件哈希值,down->dowa哈希值不同

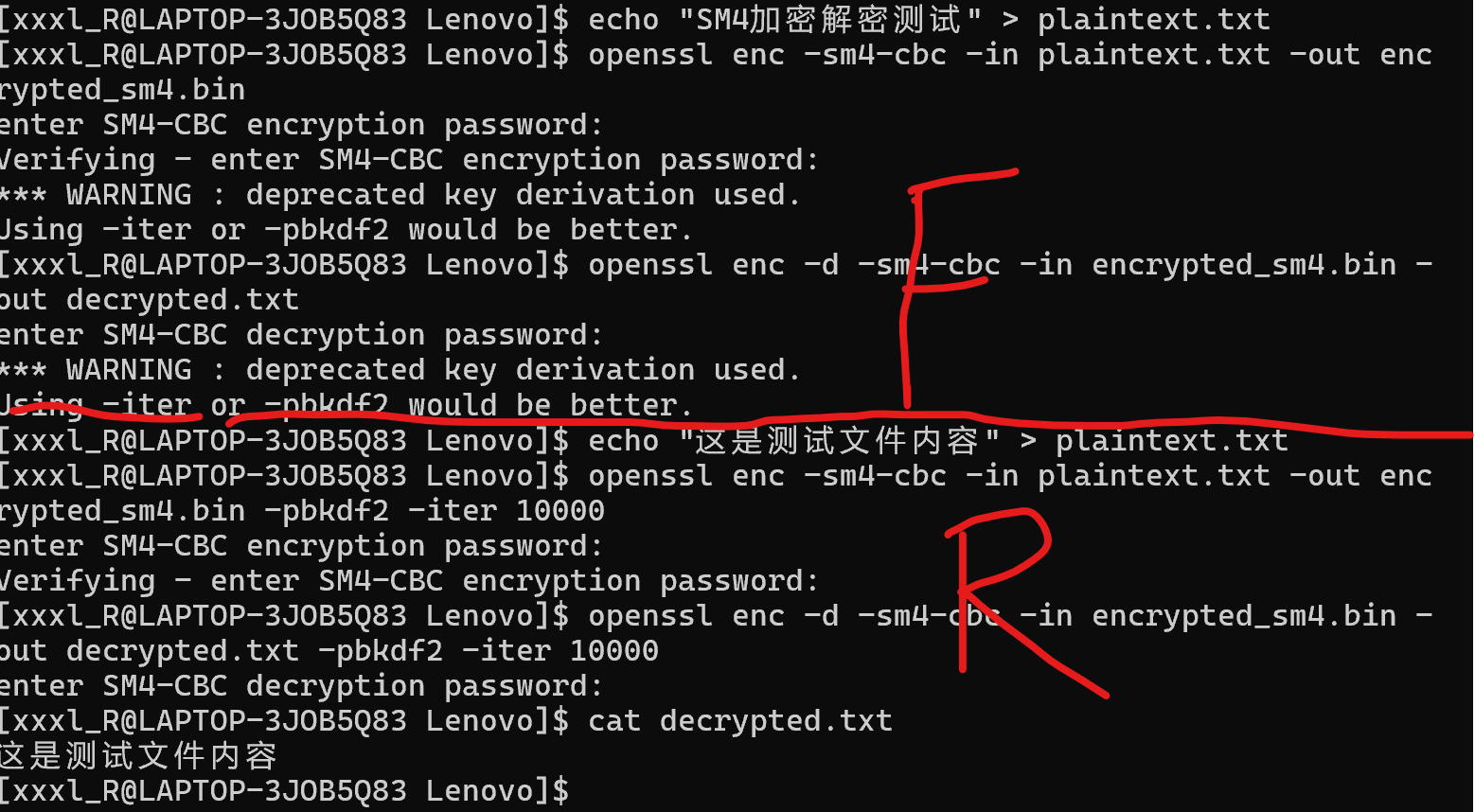
sm4测试中警告原密码过时了,采用-iter
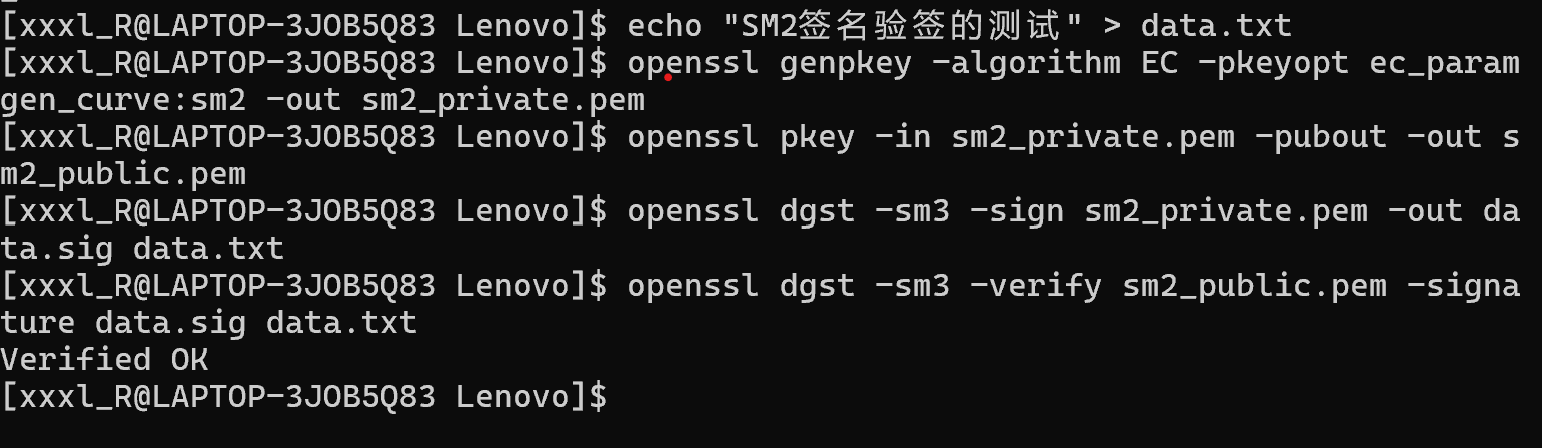
sm2数字签名

AI
无处不用,比如数学理解

感想
数学基础这些,感觉很适合高中的难题口味。想当年高中老师为了拿些高分,花费时间在难题上,琐碎的,就题而讲。笔者如同听天书,云里雾里,很焦虑,因为以当时笔者的水平,考试中根本就写不到那些题,花费时间但是没有多大成效。很羡慕那些能把答案完整写下来的同学,看来有本大学教材就够了(bushi)。现在也几乎是自学,现在缓存下来些时间,又有高效工具,很乐意去看看这些基础。
课本《网络空间安全导论(微课版)》
