luogu P8816 [CSP-J 2022] 上升点列 题解
tip:如果没有看过题,建议先点击标题中的链接看一眼题
题意简述
题目大意相信大家都能看懂(摸鱼),看懂了直接跳到思路部分即可。
如果你没有看懂题意,有下面两个题意选择:
注:以下是折叠框,请通过左边的小三角展开
1. 啰嗦而鬼畜版
这道题的题意实际上非常的简单易懂。就是在一个平面直角坐标系(如果你连这个都不知道就自行度娘)中,题中会给出神秘的互不相同 n 个整点(横纵坐标都为整数的点),此外可能是因为你获得了★全★新★的★力★量★,所以你可以自由添加 k 个整点。然后,我们把一个「好序列」定义为一个序列中每一个点的横纵坐标单调不减,即x_i=x_{i-1}+1或y_i=y_{i-1}+1,求你使用神秘的力量添加 k 个点之后能在这 n+k 个点中找出的最长的序列的长度2. 极速版
题意十分简单。题中会给出 n 个不同的在一个平面直角坐标系中的整点,并且给出你可以添加的整点数 k ,要求求出一个最长的序列的长度,其中所有的点横纵坐标单调不减,即满足x_i=x_{i-1}+1或y_i=y_{i-1}+1。思路
本题的思路也十分的简单哈,本人想了5min不到就出了(实际上写的时候还是出锅了)。
「显而易见」
显而易见,这道题求的是最长序列的长度,这是最优化问题,所以很容易想到 dp (如果不会 dp 的话出门右转oi-wiki搜动态规划即可),其次,结合题目名称“上升点列”,也不难看出,这道题的思路和LIS(最长上升子序列,不会出门右转……)有点相似。
「圆规正转」
我们言归正传,该讲这道题的具体思路了:
上 dp 四部曲!
- 状态:$dp_{i,j}$表示考虑前$i$个点,还剩$j$个可增加的点时的满足条件的最长点列长度(只考虑到以给出的某个整点,而非自己添加的整点为结尾)
- 答案:$max(dp_{i,j(1\le i\le n,0\le j\le k)}+j)$为什么要$+j$呢?因为现在还剩下$j$个点可以添加,所以肯定可以将它们全部加上来增加点列的长度
- 初值:$dp_{i,k(1\le i\le n)}=0$
- 转移:
曼哈顿前缀和数组的定义(建议看)
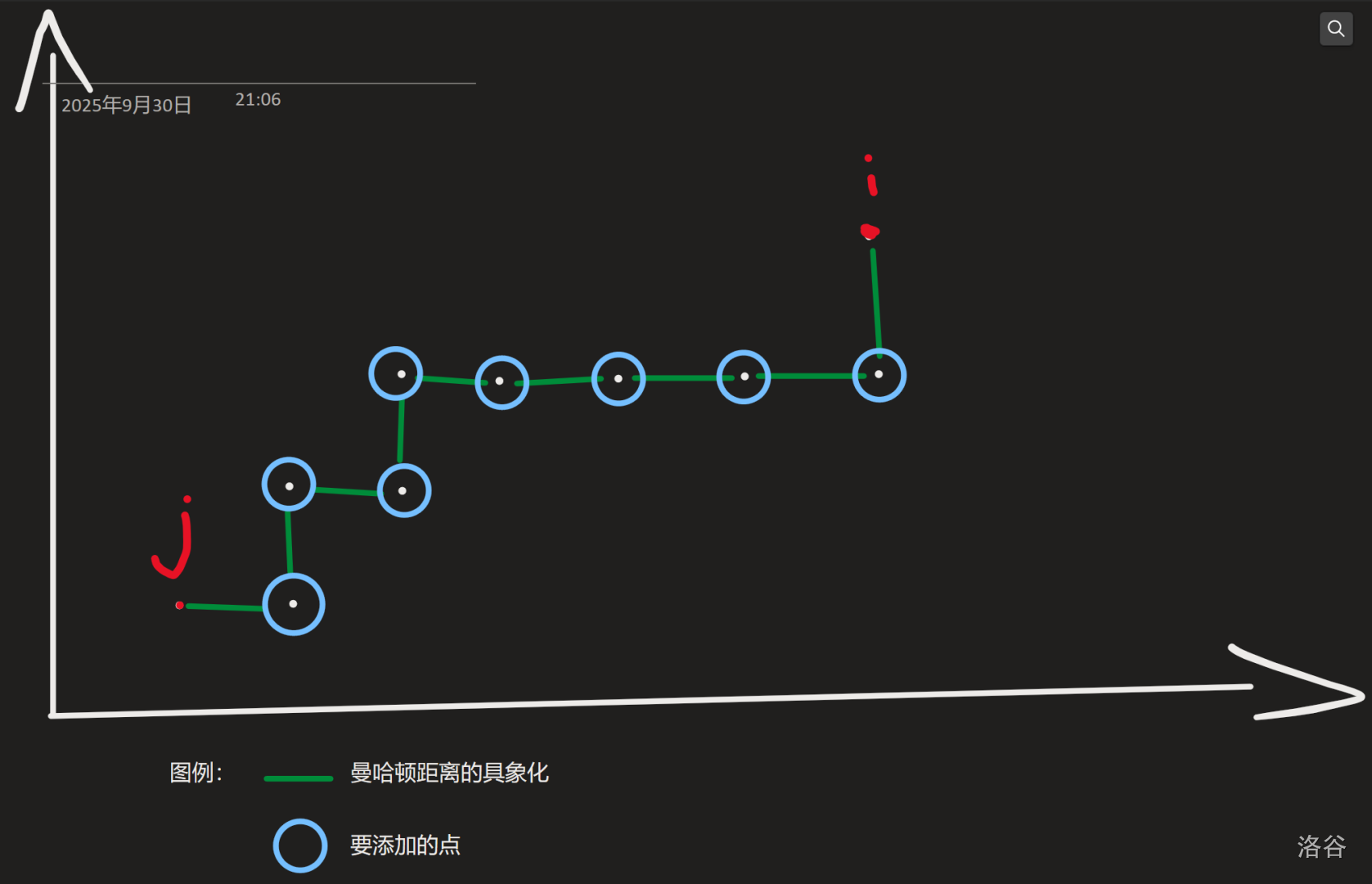
为了更为方便地求出任意两个点之间的曼哈顿距离(待会有用),我们要通过一个前缀和数组来优化区间求和(显然的) 以下是详细数组的定义: 如果我们将点 i 和 i-1 之间的曼哈顿距离记为 mht_i ,并将 mht 数组做一个前缀和,就会发现点 i 和 j (i>j)之间的曼哈顿距离为mht_i-mht_j。
如果不想看推出式子的过程的长篇大论,直接通过标签往下看即可。
>既然我换行了,说明转移稍微有一些难想。首先想到LIS是对于每一个点$i$,枚举它在序列中的上一个点$j$,然后由$j$推过来即可。所以不难想到这一道题也是如此。
>那么在预处理的时候先对这些点从低到高进行排序,$x$为第一关键字,$y$为第二关键字,这样可以使这些点稍微有一点顺序,但是还是需要特判$x$和$y$不符合条件的情况。
>这样的话,LIS中的那个“>”号的作用好像就被我们实现了啊?
>但是我们还得考虑一件十分重要的事情,那就是可以添加的那些点怎么处理。也就是说,我们如何计算从$j$到$i$需要的费用?(也就是需要添加多少个点?)
>我们不妨思考一下:首先,对于两个“相邻”的点i和j,即可以直接加入同一个序列的点,定义是这样的:满足$x_i=x_{j}+1$或$y_i=y_{j}+1$(这是题面中有说的,只不过小小的修改了一下)那我们就可以想到,两个整点的欧几里得距离为1其实跟它们两个的曼哈顿距离为1是没有区别的,而两个并不相邻的点想要构成递推的关系,要想办法将这两个点通过一些两两之间曼哈顿距离为1的点“连接”起来。
>那么要想让两个不相邻的整点$i$和$j$($i>j$)构成递推关系,需要增加$mht_i-mht_j-1$,也就是两点之间的曼哈顿距离-1个整点。
图解:
最终的状态转移方程
dp[i][q]=max(dp[i][q],dp[j][q+dis]+dis+1);
AC Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=505,K=105;
int n,k;
struct points{int x,y;
}pts[N];//存点
int mht[N];//曼哈顿前缀和
int dp[N][K];//dp数组bool cmp(points a,points b){if(a.x==b.x){return a.y<b.y;}return a.x<b.x;
}//compare函数,注意关键字signed main(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>pts[i].x>>pts[i].y;}sort(pts+1,pts+n+1,cmp);//排序for(int i=1;i<=n;i++){mht[i]=(pts[i].x-pts[i-1].x)+(pts[i].y-pts[i-1].y);mht[i]+=mht[i-1];}//预处理曼哈顿距离for(int i=1;i<=n;i++){dp[i][k]=1;//dp初值for(int q=0;q<=k;q++){for(int j=1;j<i;j++){if(pts[j].x>pts[i].x||pts[j].y>pts[i].y)continue;//特判不符合条件int dis=mht[i]-mht[j]-1;if(q+dis>k){continue;}//如果距离太远,转移不过来了就炸飞()dp[i][q]=max(dp[i][q],dp[j][q+dis]+dis+1);//转移}}}int ans=-1;for(int i=1;i<=n;i++){for(int j=0;j<=k;j++){ans=max(ans,dp[i][j]+j);//别忘了有+j}}//求最大值cout<<ans;//输出return 0;//华丽结束
}
The end
今天成功贡献了一个猎奇的题解!鄙人写的题解不是很好,望包涵。
