正睿二十连测
C
最后的 DP 比较神奇,花了至少 \(1h\) 才搞懂。
给定 \(n, k\),问有多少长度为 \(n\) 的排序能在至多 \(k\) 次 “双向冒泡排序” 后变得有序。

一个经典的套路:对于每个 \(x\),将 \(\le x\) 的数看成 \(0\),\(> x\) 的数看成 \(1\)。只要对于所有 \(x\) 都能在 \(k\) 次操作后变得有序即可。
来观察一下单向的冒泡排序:\(0 10011010 \rightarrow 000110101, 010011100 \rightarrow 000111001\),不难发现其实就是将第一个 \(1\) 挪到最后(手推)。所以依次双向冒泡排序就是将第一个 \(1\) 挪到最后,再将最后一个 \(0\) 挪到开头。
一个序列是有序的,当且仅当所有 \(0\) 都在 \(1\) 的前面。我们考虑对于从前往后第 \(i\) 个 \(1\),假设有 \(c_i\) 个 \(0\) 在他后面,那么经过 \(\min(i, c_i)\) 次双冒泡排序后所有的 \(0\) 都会跑到他前面。
因为 \(c_i\) 单调不升,所以条件转化为了对于所有 \(x\),\(c_{k + 1} \le k\)。(考试做到这里就不会了。)
实际上,这个条件还不够优秀,继续转化。因为一共有 \(x\) 个 \(0\),第 \(k + 1\) 个 \(1\) 后面最多 \(k\) 个 \(0\),所以前面至少有 \(x - k\) 个 \(0\)。即前 \(x\) 个数里面至多有 \(k\) 个 \(1\)。
接下来就是 DP 了。对于 \(x = n\),显然所有数都是 \(0\),考虑从 \(n\) 到 \(1\) 一个一个的把 \(i\) 插进来(把某个数变成 \(0\))。
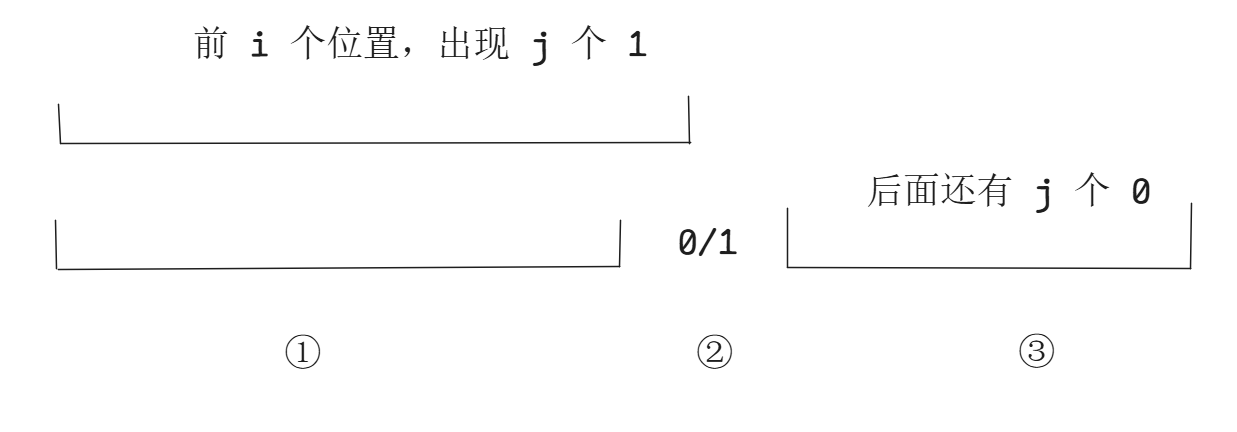
令 \(dp_{i, j}\) 表示插入了 \(i + 1 \sim n\),前 \(i\) 个位置中有 \(j\) 个 \(1\)。(\(i + 1 \sim n\) 的位置为 \(1\),其他的位置为 \(0\))。初始 \(dp_{n, 0} = 1\),答案为 \(dp_{0, 0}\)。
分第 \(i\) 个位置是 \(0/1\) 以及 \(i\) 插入到 \(1, 2, 3\) 哪个部分转移。(因为插入到 \(1\) 部分时不同的位置会有不同的转移,而且可能把两个数插到同一个位置。只能采取延后贡献得方式,具体插入到哪个先不管。)
- 若第 \(i\) 个位置为 \(0\),插入到 \(1\) 部分:\(dp_{i, j} \rightarrow dp_{i - 1, j + 1}\)。
- 若第 \(i\) 个位置为 \(0\),插入到 \(3\) 部分:\(dp_{i, j} \times j \rightarrow dp_{i - 1, j}\),从 \(3\) 部分选择一个 \(0\) 的位置。
- 若第 \(i\) 个位置为 \(0\),插入到 \(2\) 部分:\(dp_{i, j} \rightarrow dp_{i - 1, j}\)。
- 若第 \(i\) 个位置为 \(1\),要从 \(j\) 个数里挑一个填到 \(i\) 的位置。(延后贡献造成的)
- 插入到 \(1\) 部分:\(dp_{i, j} \times j \rightarrow dp_{i - 1, j}\)。
- 插入到 \(3\) 部分:\(dp_{i, j} \times j^2 \rightarrow dp_{i - 1, j - 1}\)。还有一个 \(j\) 和第二条一样。
时间复杂度 \(O(nk)\)。
实际代码只有二十几行。
本题要先想到对于将排列转化为 \(01\) 序列的常用技巧,将条件转化成可以 DP 的式子。然后 DP 时需要用到延后贡献的思想。
