感觉这个东西有点抽象啊,三道题下来也不是很懂的样子
前置知识
线段树(or树状数组),离散化
解决目标
矩形面积并,矩形周长并,二位数点覆盖等
矩形面积并
先看例题 矩形面积比
大意:给定n个矩形,求这n个矩形的并集覆盖的总面积
由于坐标值域一般极大,我们要考虑一种快速求面积交的方法,容易发现对于一个矩形并集的图像,我们可以将其分成若干个小矩形,对于每个小矩形,我们只需要知道他的长和宽就可以快速求出它的面积;
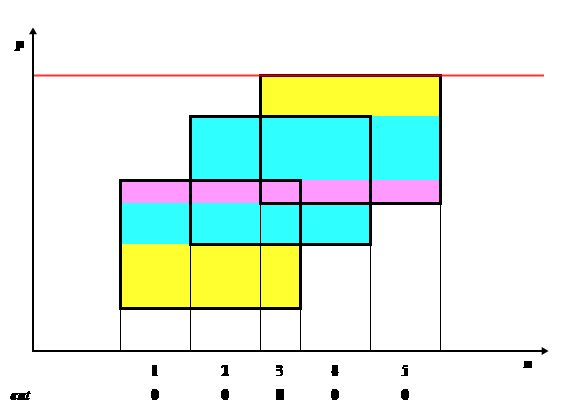
借用OIWIKI的图,我们记录每个初始矩形的上下两条边,以及其左右边界。从下往上扫描,若本次扫到下边界,就将其覆盖的左右区间内全部+1,反之则-1;
当然因为值域巨大,所以我们要先把左右边界离散化处理;因为两个相邻的左右边界内的操作是统一进行的,所以每两个相邻左右边界中的区间放到线段树上就是单位1的长度,这里为了方便存储,对于每条线段,我们都将它的右边界-1以方便操作
最终我们从下往上扫描每条线段并进行区间修改,统计时,只需要统计整棵线段树内值不为0的区间总长度(注意这里不是节点个数了,是放到图像上的实际区间长度)乘上距离上一个线段的纵向距离,就是本次的答案,最后累加即可;
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=2e5+10;
struct node{int x,l,r;int tag;
}line[MAXN<<1];
int n,tot,b[MAXN<<1],cnt,tr_b[MAXN<<1];
map<int,int> mp;
bool cmp(node a,node b){return (a.x!=b.x?a.x<b.x:a.tag>b.tag);
}
struct tree{int sum,l,r,tag;
}tr[MAXN<<4];
#define ls id<<1
#define rs id<<1|1
void build(int id,int l,int r){tr[id].l=l,tr[id].r=r;tr[id].sum=tr[id].tag=0;if(l==r) return ;int mid=l+r>>1;build(ls,l,mid);build(rs,mid+1,r);return ;
}
void pushup(int id){if(!tr[id].tag){tr[id].sum=tr[ls].sum+tr[rs].sum;return ;}tr[id].sum=tr_b[tr[id].r+1]-tr_b[tr[id].l];return ;
}
void add(int id,int l,int r,int val){if(tr[id].l>r||tr[id].r<l) return ;if(tr[id].l>=l&&tr[id].r<=r){tr[id].tag+=val;if(tr[id].tag) tr[id].sum=tr_b[tr[id].r+1]-tr_b[tr[id].l];else pushup(id);return ;}add(ls,l,r,val);add(rs,l,r,val);pushup(id);return ;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);cin>>n;for(int i=1,xf,yf,xs,ys;i<=n;i++){cin>>xf>>yf>>xs>>ys;line[++tot].x=xf;line[tot].l=yf,line[tot].r=ys;line[tot].tag=1;line[++tot].x=xs;line[tot].l=yf,line[tot].r=ys;line[tot].tag=-1;}n=tot,tot=0;for(int i=1;i<=n;i+=2){b[++tot]=line[i].l;b[++tot]=line[i].r;}sort(b+1,b+tot+1);for(int i=1;i<=tot;i++){if(!mp[b[i]]){mp[b[i]]=++cnt;tr_b[cnt]=b[i];}}for(int i=1;i<=n;i++){line[i].l=mp[line[i].l];line[i].r=mp[line[i].r];}sort(line+1,line+n+1,cmp);int ans=0;build(1,1,n);for(int i=1;i<=n;i++){
// cout<<tr[1].sum<<" "<<line[i].x<<" "<<line[i-1].x<<"\n";if(i!=1) ans+=tr[1].sum*(line[i].x-line[i-1].x);
// cout<<line[i].l<<" "<<line[i].r<<" "<<line[i].tag<<"\n"; add(1,line[i].l,line[i].r-1,line[i].tag);} cout<<ans;return 0;
}
矩阵周长并
例题:矩形周长并
相对于面积并,这道题可能还要简单一点。容易发现对于两条相邻的线段,增加的周长长度就是其差的绝对值,只需要横着扫一遍,竖着再扫一遍即可;
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=5e3+10,INF=1e4;
int n,trn,tot,b[MAXN<<2],tr_b[MAXN<<2],cnt;
int ans,lst_sum;
struct ng{int xf,yf,xs,ys;
}init[MAXN];
struct node{int x,tag,l,r;
}line[MAXN<<2];
bool cmp(node a,node b){return (a.x!=b.x?a.x<b.x:a.tag>b.tag);
}
map<int,int> mp;
struct tree{int l,r,sum,tag;//tag用来记录这段区间有没有被整体覆盖,如果被整体覆盖过直接求sum即可,否则从左右儿子获得信息
}tr[MAXN<<4];
#define ls id<<1
#define rs id<<1|1
void build(int id,int l,int r){tr[id].l=l,tr[id].r=r;tr[id].sum=tr[id].tag=0;if(l==r) return ;int mid=l+r>>1;build(ls,l,mid);build(rs,mid+1,r);return ;
}
void pushup(int id){if(!tr[id].tag){tr[id].sum=tr[ls].sum+tr[rs].sum;return ;}tr[id].sum=tr_b[tr[id].r+1]-tr_b[tr[id].l];return ;
}
void add(int id,int l,int r,int val){if(tr[id].l>r||tr[id].r<l) return ;if(l<=tr[id].l&&tr[id].r<=r){tr[id].tag+=val;if(tr[id].tag) tr[id].sum=tr_b[tr[id].r+1]-tr_b[tr[id].l];else pushup(id);return ;}
// int mid=tr[id].l+tr[id].r>>1;add(ls,l,r,val);add(rs,l,r,val);pushup(id);return ;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);cin>>n;trn=n;for(int i=1;i<=n;i++){cin>>init[i].xf>>init[i].yf>>init[i].xs>>init[i].ys;init[i].xf+=INF,init[i].xs+=INF,init[i].yf+=INF,init[i].ys+=INF;}for(int i=1;i<=n;i++){line[++tot].x=init[i].xf;line[tot].l=init[i].yf,line[tot].r=init[i].ys;line[tot].tag=1;line[++tot].x=init[i].xs;line[tot].l=init[i].yf,line[tot].r=init[i].ys;line[tot].tag=-1;}n=tot,tot=0;for(int i=1;i<=n;i+=2){b[++tot]=line[i].l;b[++tot]=line[i].r;}sort(b+1,b+tot+1);for(int i=1;i<=tot;i++){if(!mp[b[i]]){mp[b[i]]=++cnt;tr_b[cnt]=b[i];}}for(int i=1;i<=n;i++){line[i].l=mp[line[i].l];line[i].r=mp[line[i].r];}sort(line+1,line+n+1,cmp);build(1,1,n);for(int i=1;i<=n;i++){
// cout<<line[i].l<<" "<<line[i].r<<" ";add(1,line[i].l,line[i].r-1,line[i].tag);
// cout<<lst_sum<<" "<<tr[1].sum<<"\n";ans+=abs(tr[1].sum-lst_sum);lst_sum=tr[1].sum;}tot=0,n=trn,cnt=0;mp.clear();for(int i=1;i<=n;i++){line[++tot].x=init[i].yf;line[tot].l=init[i].xf,line[tot].r=init[i].xs;line[tot].tag=1;line[++tot].x=init[i].ys;line[tot].l=init[i].xf,line[tot].r=init[i].xs;line[tot].tag=-1;}n=tot,tot=0;for(int i=1;i<=n;i+=2){b[++tot]=line[i].l;b[++tot]=line[i].r;}sort(b+1,b+tot+1);for(int i=1;i<=tot;i++){if(!mp[b[i]]){mp[b[i]]=++cnt;tr_b[cnt]=b[i];}}for(int i=1;i<=n;i++){line[i].l=mp[line[i].l];line[i].r=mp[line[i].r];}sort(line+1,line+n+1,cmp);build(1,1,n);for(int i=1;i<=n;i++){
// cout<<line[i].l<<" "<<line[i].r<<" ";add(1,line[i].l,line[i].r-1,line[i].tag);
// cout<<lst_sum<<" "<<tr[1].sum<<"\n";ans+=abs(tr[1].sum-lst_sum);lst_sum=tr[1].sum;}cout<<ans;return 0;
}
其实选定一个方向后,每次更新答案时同时加上两条高的贡献可以单次扫描解决这道题,但主播太懒了不想写(不想动脑
二维数点覆盖
例题:窗口的星星
我们发现对于二维平面内的散点并不好计算,但是我们可以把每个点扩充成一个w*h的矩形(因为题目中说了边界不算,所以实际要给坐标-1),对于这个抽象矩形内的所有点附上权值;
我们容易发现,只要两个点扩充的矩形有交,就代表可以用一个窗口将两个点同时框住;
那么事情就非常好办了,我们仍然采用传统扫描线的方法,在每次区间修改后找出整棵线段树上的最大值,也就是相交矩形权值和最大的部分,求max即可;
代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+10;
int T,n,w,h,cnt,b[MAXN<<1],tr_b[MAXN<<1],tot;
map<int,int> mp;
struct node{int x,y,l;
}e[MAXN];
struct le{int x,l,r,vl;
}line[MAXN<<1];
bool cmp(le x,le y){return (x.x!=y.x?x.x<y.x:x.vl>y.vl);
}
struct tree{int l,r,maxn,tag;
}tr[MAXN<<2];
#define ls id<<1
#define rs id<<1|1
void build(int id,int l,int r){tr[id].l=l,tr[id].r=r,tr[id].maxn=tr[id].tag=0;if(l==r) return ;int mid=l+r>>1;build(ls,l,mid);build(rs,mid+1,r);return ;
}
void pushup(int id){tr[id].maxn=max(tr[ls].maxn,tr[rs].maxn);return ;
}
void pushdown(int id){if(tr[id].tag){tr[ls].maxn+=tr[id].tag;tr[rs].maxn+=tr[id].tag;tr[ls].tag+=tr[id].tag;tr[rs].tag+=tr[id].tag;tr[id].tag=0;}return ;
}
void add(int id,int l,int r,int val){if(tr[id].l>r||tr[id].r<l) return ;if(l<=tr[id].l&&tr[id].r<=r){tr[id].maxn+=val;tr[id].tag+=val;return ;}pushdown(id);int mid=tr[id].l+tr[id].r>>1;if(l<=mid) add(ls,l,r,val);if(r>mid) add(rs,l,r,val);pushup(id);return ;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);cin>>T;while(T--){cin>>n>>w>>h;if(w==1||h==1){cout<<"0\n";}for(int i=1;i<=n;i++){cin>>e[i].x>>e[i].y>>e[i].l;++cnt;line[cnt].x=e[i].x;line[cnt].l=e[i].y,line[cnt].r=e[i].y+h-1;line[cnt].vl=e[i].l;++cnt;line[cnt].x=e[i].x+w-1;line[cnt].l=e[i].y,line[cnt].r=e[i].y+h-1;line[cnt].vl=-1*e[i].l;}n=cnt,cnt=0;for(int i=1;i<=n;i+=2){b[++cnt]=line[i].l;b[++cnt]=line[i].r;}sort(b+1,b+n+1);for(int i=1;i<=cnt;i++){if(!mp[b[i]]){mp[b[i]]=++tot;tr_b[tot]=b[i];}}for(int i=1;i<=n;i++){line[i].l=mp[line[i].l];line[i].r=mp[line[i].r];}sort(line+1,line+n+1,cmp);build(1,1,tot);long long ans=0;for(int i=1;i<=n;i++){add(1,line[i].l,line[i].r,line[i].vl);ans=max(ans,tr[1].maxn);}cout<<ans<<"\n";mp.clear();cnt=tot=0;}return 0;
}
