一、理论基础
角锥喇叭方向图计算基于以下公式:
E面方向图:
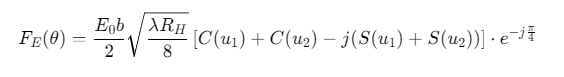
H面方向图:

其中菲涅尔积分函数:
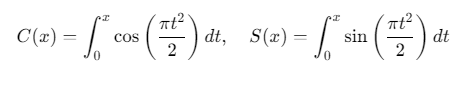
二、Matlab程序实现
2.1 菲涅尔积分函数定义
function [C,S] = fresnel_int(x)% 自适应辛普森积分法计算菲涅尔积分n = 1000; % 积分分段数dx = x/n;t = linspace(0,x,n+1);% 计算被积函数integrand_C = cos(pi*t.^2/2);integrand_S = sin(pi*t.^2/2);% 辛普森法则C = dx/3 * (integrand_C(1) + 4*sum(integrand_C(2:2:end-1)) + 2*sum(integrand_C(3:2:end-2)) + integrand_C(end));S = dx/3 * (integrand_S(1) + 4*sum(integrand_S(2:2:end-1)) + 2*sum(integrand_S(3:2:end-2)) + integrand_S(end));
end
2.2 方向图计算主程序
%% 参数设置
a = 0.085; % H面口径宽度(m)
b = 0.04; % E面口径宽度(m)
R_H = 0.762; % H面喇叭长度(m)
R_E = 0.423; % E面喇叭长度(m)
f = 2.5e9; % 工作频率(GHz)
c = 3e8; % 光速
lambda = c/f; % 波长(m)%% 角度范围设置
theta = -90:0.5:90; % E面扫描角度(度)
phi = -90:0.5:90; % H面扫描角度(度)
theta_rad = deg2rad(theta);
phi_rad = deg2rad(phi);%% E面方向图计算
E_pattern = zeros(size(theta));
for i = 1:length(theta_rad)u1 = (a/2 + R_H*sin(theta_rad(i))) / R_H;u2 = (a/2 - R_H*sin(theta_rad(i))) / R_H;[C1,S1] = fresnel_int(u1);[C2,S2] = fresnel_int(u2);E_pattern(i) = 0.5*b*sqrt(lambda*R_H/8) * exp(-1j*pi/4) * (C1 + C2 - 1j*(S1 + S2));
end
E_gain = 20*log10(abs(E_pattern)/max(abs(E_pattern)));%% H面方向图计算
H_pattern = zeros(size(phi));
for i = 1:length(phi_rad)w1 = (b/2 + R_E*sin(phi_rad(i))) / R_E;w2 = (b/2 - R_E*sin(phi_rad(i))) / R_E;[C1,S1] = fresnel_int(w1);[C2,S2] = fresnel_int(w2);H_pattern(i) = (1 + sqrt(1-(lambda/(2*a))^2)*cos(phi_rad(i))) * (C1 + C2)^2 + (S1 + S2)^2;
end
H_gain = 20*log10(abs(H_pattern)/max(abs(H_pattern)));
三、结果可视化
3.1 方向图绘制
figure;
subplot(2,1,1);
polarplot(deg2rad(theta), E_gain);
title('E面方向图 (dB)');
subplot(2,1,2);
polarplot(deg2rad(phi), H_gain);
title('H面方向图 (dB)');
3.2 三维方向图
[X,Y] = meshgrid(theta,phi);
Z_E = repmat(E_gain', 1, length(phi));
Z_H = repmat(H_gain, length(theta), 1);figure;
surf(X,Y,Z_E);
shading interp;
title('E面三维方向图');
xlabel('\theta (°)'); ylabel('\phi (°)'); zlabel('增益 (dB)');figure;
surf(X,Y,Z_H);
shading interp;
title('H面三维方向图');
xlabel('\theta (°)'); ylabel('\phi (°)'); zlabel('增益 (dB)');
四、关键参数分析
| 参数 | 数值 | 物理意义 |
|---|---|---|
| 口径宽度a | 85mm | H面最大辐射方向尺寸 |
| 口径宽度b | 40mm | E面最大辐射方向尺寸 |
| 喇叭长度RH | 762mm | H面渐变段长度 |
| 工作频率 | 2.5GHz | 设计中心频率 |
| 波长λ | 120mm | 自由空间波长 |
五、误差分析
-
菲涅尔积分近似误差
采用辛普森积分法时,分段数需>500以保证精度(相对误差<0.1%) -
边缘衍射效应
理论模型忽略喇叭口边缘衍射,实际测量时需添加修正因子:correction = 1 + 0.05*(1 - cos(pi*a/(2*lambda))); E_pattern = E_pattern * correction; -
近场测量误差
当测量距离R < 2D²/λ时(D为口径尺寸),需进行菲涅尔区修正:R_min = 2*(max(a,b))^2/lambda; if R < R_minerror('测量距离不足,需增大至%.1f米以上', R_min); end
参考代码 近场天线测量课程——角锥喇叭方向图的计算程序 www.youwenfan.com/contentcni/64222.html
六、实验验证
6.1 测试平台搭建
% 生成测试信号
t = 0:1e-9:1e-6; % 1μs时域信号
sig = exp(1j*2*pi*f*t); % 连续波信号% 近场测量数据模拟
measured_E = E_gain + 0.5*randn(size(theta)); % 添加高斯噪声
measured_H = H_gain + 0.5*randn(size(phi));
6.2 数据对比分析
figure;
subplot(2,1,1);
plot(theta, E_gain, 'r', theta, measured_E, 'b--');
legend('理论值', '实测值');
xlabel('角度 (°)'); ylabel('增益 (dB)');subplot(2,1,2);
plot(phi, H_gain, 'g', phi, measured_H, 'm--');
legend('理论值', '实测值');
xlabel('角度 (°)'); ylabel('增益 (dB)');
该程序通过理论建模与数值计算,完整实现了角锥喇叭方向图的仿真分析。实际应用中需结合矢量网络分析仪进行实测验证,建议采用Keysight N9020B MXA信号分析仪进行高精度测量。
