题解:B4410 [GESP202509 一级] 金字塔
题目传送门
题意
给定正整数 \(n\),求从 \(1\) 到 \(n\) 的立方和(\(\sum \limits _{i=1} ^{n} i^2\))
数据规模与约定
\(1 \le n \le 50\)
算法 tag
模拟(循环结构),数学
题解
做法1:直接枚举求和
很简单,写个 for 循环枚举 \(1\) 到 \(n\),把每个数的平方加入 \(ans\) 中即可。
Code
void Solve(void)
{int n;cin>>n;long long ans=0;for(int i=1;i<=n;i++)ans+=i*i;cout<<ans;
}
做法2:数学公式法
对于 \(1\) 到 \(n\) 的平方和,有一个公式可以直接套用:
\[\sum \limits _{i=1} ^{n} i^2 = \frac{n(n+1)(2n+1)}{6}
\]
公式推导(三角形法):
我们可以构造一个各个位置上数字之和为 \(\sum \limits _{i=1} ^{n} i^2\) 的三角形,如下:
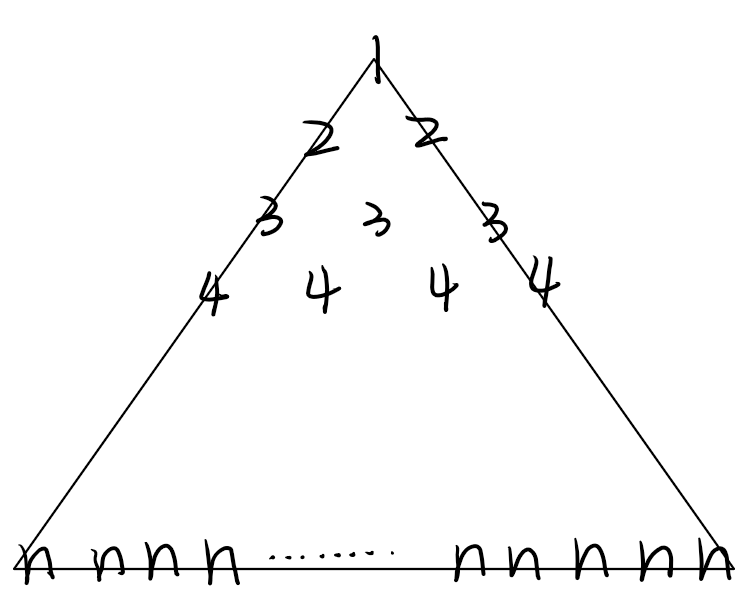
然后旋转两次后得到三个三角形(如下):
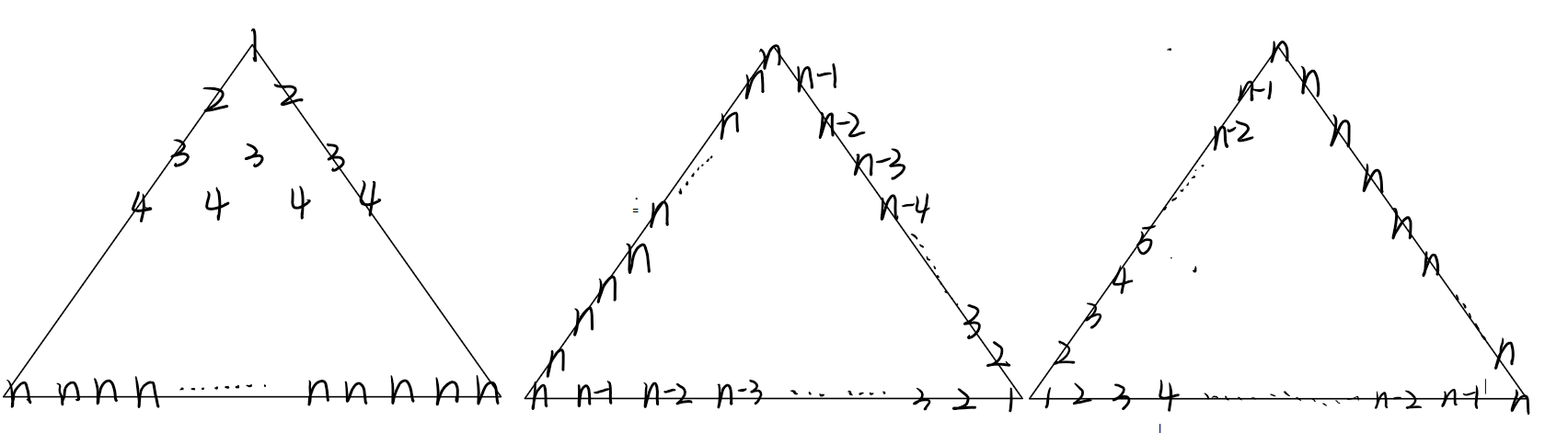
把每个位置上的数字加起来,得到:
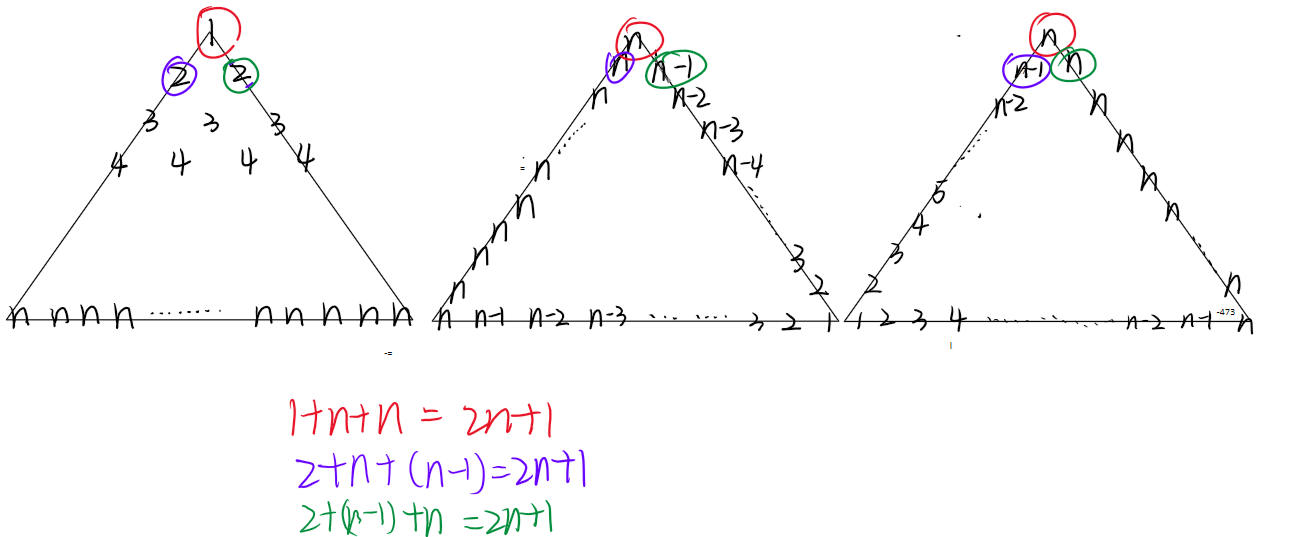
可以发现,三角形上的每一个位置上三个数的和是 \(2n+1\),一共有 \(1+2+3+4+\cdots +n=\frac{n(n+1)}{2}\) 个数字,总和就是 \((2n+1)\times\frac{n(n+1)}{2}=\frac{n(n+1)(2n+1)}{2}\),但是这是三个三角形的数字之和,我们只需要一个,所以需要把结果 \(\div 3\),得到的结果就是 \(\frac{n(n+1)(2n+1)}{2} \div 3 = \frac{n(n+1)(2n+1)}{6}\)。
所以,我们就证明出了 \(\sum \limits _{i=1} ^{n} i^2 = \frac{n(n+1)(2n+1)}{6}\)。
有了这个公式,代码就很简单啦。
Code
void Solve(void)
{int n;cin>>n;long long ans=(n*(n+1)*(2*n+1))/6;cout<<ans;
}
