Part 1 题目
题目: 点击这里快速下载
Part 2 考试重大时间线
8:00 开题,却发现题做过了(当然不是我做过),延迟十分钟。
8:10 再次开题,立刻开T1,认为就是一个简单的dijkstra,于是直接开写。
8:50 样例随便过,大样例TLE飞了,于是加了一个神秘的估价函数,时间复杂度不详,但大样利秒过,认为包没有问题的,没想到是大样例太水了。
9:20 读完题后,先写了一个Tarjan,又是熟悉的样例随便过,大样例**TLE**飞了,然后想其他解法。
9:50 仔细研究了大样例后,发现整张图只有两个强连通分量,只需要将不是连接同一个强连通分量便可以\(\color{green} Accepted\) 于是又是轻松过大样例,由于这道题用的时间有点长,就先看下一题。
10:30 终于看懂T3题面之后,先写了一个完全不用脑子的暴力,然后发现除了样例,啥都出不来,加了个记忆化,过了 \(\color{red} 20\) 分的点。
11:20 T4写了一个暴力,发现这次连样例都过不了了,于是直接输出大样例,骗了十分。
12:10 后来又转头回去看T2,终于发现了原来的办法除了能过大样例其他什么都过不了,最后关头写了一个跟TJ思路有几分相像的代码,也就比暴力分高几分。
Part 3 题目详解
T1
dijkstra 当然没有错,优化的主要是在一个节点停留时间的选择。
先说结论:
设t为 到这个节点+等待的时间。
设t'为 到下一个节点的时间。
得到:
设
则对这个函数求导得:
所以当\(f'(t)=0\)。
所以我们只需要每一次转移到:
(因为有可能不能到\(\sqrt b\))
#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e5+5;
int n,m;
int dis[N];
int vis[N];
struct node{int y,c,d;};
vector<node> v[N];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void Dij(){priority_queue<PII> Q;Q.push({0,1});while(!Q.empty()){int x=Q.top().second;int t=-Q.top().first;Q.pop();if(x==n){cout<<t;exit(0);}if(vis[x]) continue;vis[x]=1;for(node y: v[x]){int num=1e18;int nt=max(t,(int)sqrt(y.d));Q.push({-nt-y.c-(y.d/(nt+1)),y.y});}}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);freopen("road.in","r",stdin);freopen("road.out","w",stdout);cin>>n>>m;for(int i=1;i<=m;i++){int a,b,c,d;cin>>a>>b>>c>>d;v[a].push_back({b,c,d});v[b].push_back({a,c,d});}Dij();cout<<-1;return 0;
}
T2
这道题目我们可以分两种情况讨论:
- 这条边在一个强连通分量重
- 这条边连接着两个强连通分量
【情况一】
我们发现在这里可以简单的画出输出same和diff的情况
same: 对于边 (1,8)
diff: 对于边 (2,3)
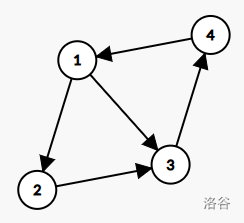
我们可以发现:
【出现same】对于边 (a,b) 若除了边 (a,b) 有 路径a-b 联通 则这条边没有影响
【出现diff】对于边 (a,b) 若除了边 (a,b) 所有其他 路径a-b 都不联通 则这条边有影响
【情况二】
same: 对于边 (6,7)
diff: 对于边 (6,2),(5,1)
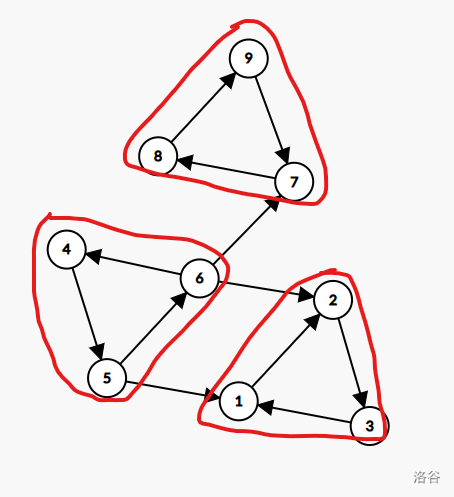
我们可以发现:
【出现same】对于边 (a,b) 若除了边 (a,b) 有 路径a-b 联通 则这条边有影响
【出现diff】对于边 (a,b) 若除了边 (a,b) 所有其他 路径a-b 都不联通 则这条边没有影响
总结:
由于【情况一】满足一定有 路径b-a,而【情况二】满足一定没有 路径b-a。
因而答案为: 若同时存在 a-b 和 b-a 或同时不存在,则为same。
于是完了\(\color{white} 吗?\)
本题重点!!!
因为不太好回避原本的边,因而把有关 路径a-b有 改为 路径a-b数量大于一(且路径不相同)。
因而从一个节点出发时,枚举走的第一个点,一次正序,一次倒叙,如果两次出发的点相同,则只有一条路径。
T3
推的实在是太好看了。
额······
T4
没啥好说的,但是交大样例竟然有十分。
Part 4 总结
| 题目 | 预期得分 | 实际得分 | 主要算法 | 失分原因 | 改进方法 |
|---|---|---|---|---|---|
| 不稳定的道路 | 100 | 21 | dijkstra+数学 | 由于大样例太水,完全没看出代码的问题 | 仔细算好时间复杂度 |
| 翻转有向图 | 24+ | 28 | 思维+dfs | 如果看预期的分的话,实际的分还高几分,但是可惜了,考场上一共写了三种做法,也是只有暴力得了分 | ··· |
| 在表格里造序列 | 20 | 20 | 数学+杜教筛 | 没推出式子 | ··· |
| zzzyyds | 0 | 10 | DP+组合数学 | 额。还多了十分(大样例) | ··· |
总分: 79
预期得分:144
