风力发电机输出功率模型综述 - 详解
摘要:在设计最优环境时,准确的建模是十分关键的。影响风机性能的主要因素是风速分布、轮毂高度以及所选风力机的功率输出曲线,故在进行风机建模时必须适当考虑这些因素。本文对风机输出功率建模的各种方法进行了详细的介绍。基于风能基本方程的建模方法使用时较繁琐,而且无法正确地复现实际风机的特性。基于假定功率曲线的建模方法虽然使用较为简单,但也缺乏准确性,不过当年平均风速较高时,表现出较为满意的响应。采用风机实际功率曲线建立特征方程的建模途径,当风机功率曲线光滑时,最小二乘法和三次样条插值法均能得到准确的结果,而对于功率曲线不太光滑的风机,采用基于最小二乘法的模型是最合适的。
关键词:风力发电机,数学建模,功率曲线,最小二乘法,三次样条插值,风速分布
1 引言
全球的经济与科技飞速发展,各行各业对能源的需求不断增加。各国都在积极寻求更高效、更清洁的可持续能源解决方案。在此社会环境下,我国提出双碳减排目标,构建新型电力系统提高能源利用效率[1]。截止 2024 年 6 月,我国新能源发电装机容量达到了 11.8 亿千瓦,其中光伏发电和风力发电分别为 4.7 亿千瓦和 7.1 亿千瓦,占总装机容量的 38.4%,新能源发电装机规模首次超过煤电[2]。
受各种环境因素的影响,风能的不稳定性,使得风力发电系统输出功率随气象条件的变化而不断变化,且存在间歇性。设计良好的能源系统具有成本效益与可靠性,而系统组成部分的精确建模是其优化的关键。显然,了解影响系统性能的所有因素是准确建模的先决条件。影响风力机功率输出的三个主要因素是:风速分布、轮毂塔高和功率输出曲线。本文首先讨论了这些因素对风力发电机性能的影响,并在次基础上,对风机输出功率建模的各种方法进行了详细的介绍[3]。
2 风能转换系统基础
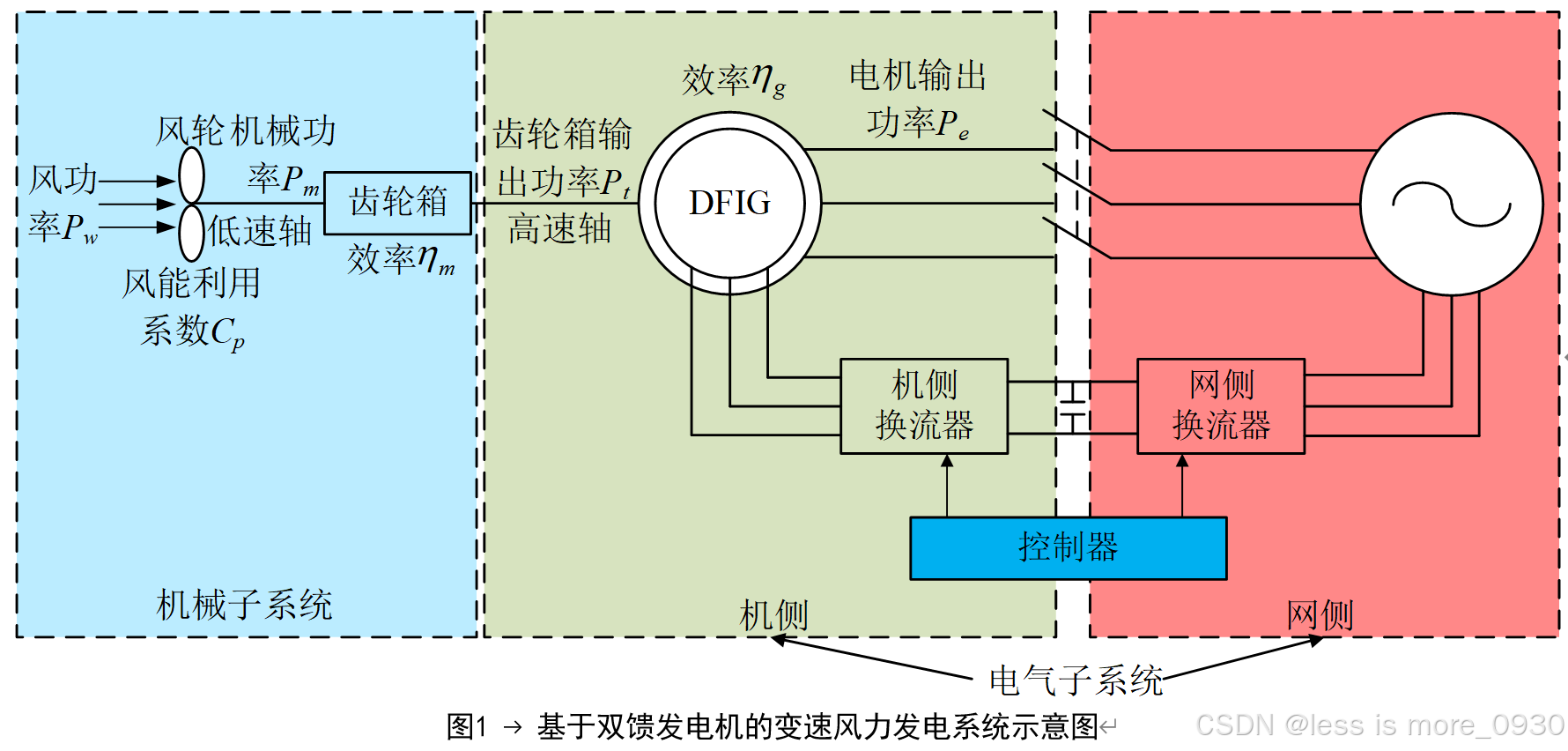
图1为基于双馈异步风力发电机的变速风力发电系统示意图,从其中可能提取出风能转换系统(Wind energy Conversion System,WECS)的基本功率级如图2所示[4]。

在垂直风速为v、空气密度为ρa的气流的横截面积A内,由风能功率方程可得瞬时风功率的表达式为[5-6]:

式中,Pw 为风功率;ρa为空气密度;A为横截面积;v为截面上的垂直风速。
该风功率通过风力机转化为机械功率Pm:
![]()
式中,Pm为风功率转化而来的机械功率;Cp为风能利用系数。
之后,将这种机械动力提供给机械传动系统(齿轮等),机械传动环境的输出,即Pt作为输入馈送给发电机:
![]()
式中,Pt为机械传动架构的输出功率;hm为机械传动环境的传输效率。
接着,得到发电机的输出功率为:
![]()
式中,Pe为风力发电机输出的电功率;hg为风力发电机的发电效率。
综上所示,整个风能转换系统的输出功率为:
![]()
式(5)中括号内的项表示风能转换系统的总效率(h0)。因此,输出功率的表达式又可写为:
![]()
3 影响风力机输出功率的因素
决定风力机功率输出的关键因素有三个:所选风力机安装地点的风速分布、轮毂高度以及所选风力机的功率输出曲线(由风能利用系数Cp、机械传动效率hm和发电机效率hg 决定)。
3.1 选定地点的风速分布
计算风力发电机输出所需的最关键内容。众所周知,风速随着分钟、小时、天、季节甚至年而变化;因此,为了准确地预测风力发电机的发电量,需要现场的风速分布情况。通过对世界上许多地点风速变化的长期研究发现,用威布尔概率分布函数就是由风能功率方程可知,风力发电机的输出功率正比于风速的三次方;因此,特定地点的风速f(v) 来描述风速的分布是最适合的[7-8]。
如果风速 v 的概率密度函数如式(7)所示,则其为威布尔分布。
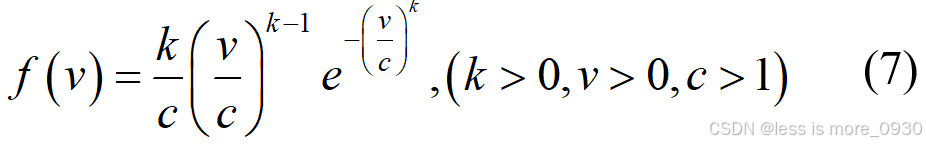
可以将风速v的概率密度函数乘以8760,以表示某一特定风速在一年中可能出现的时长。
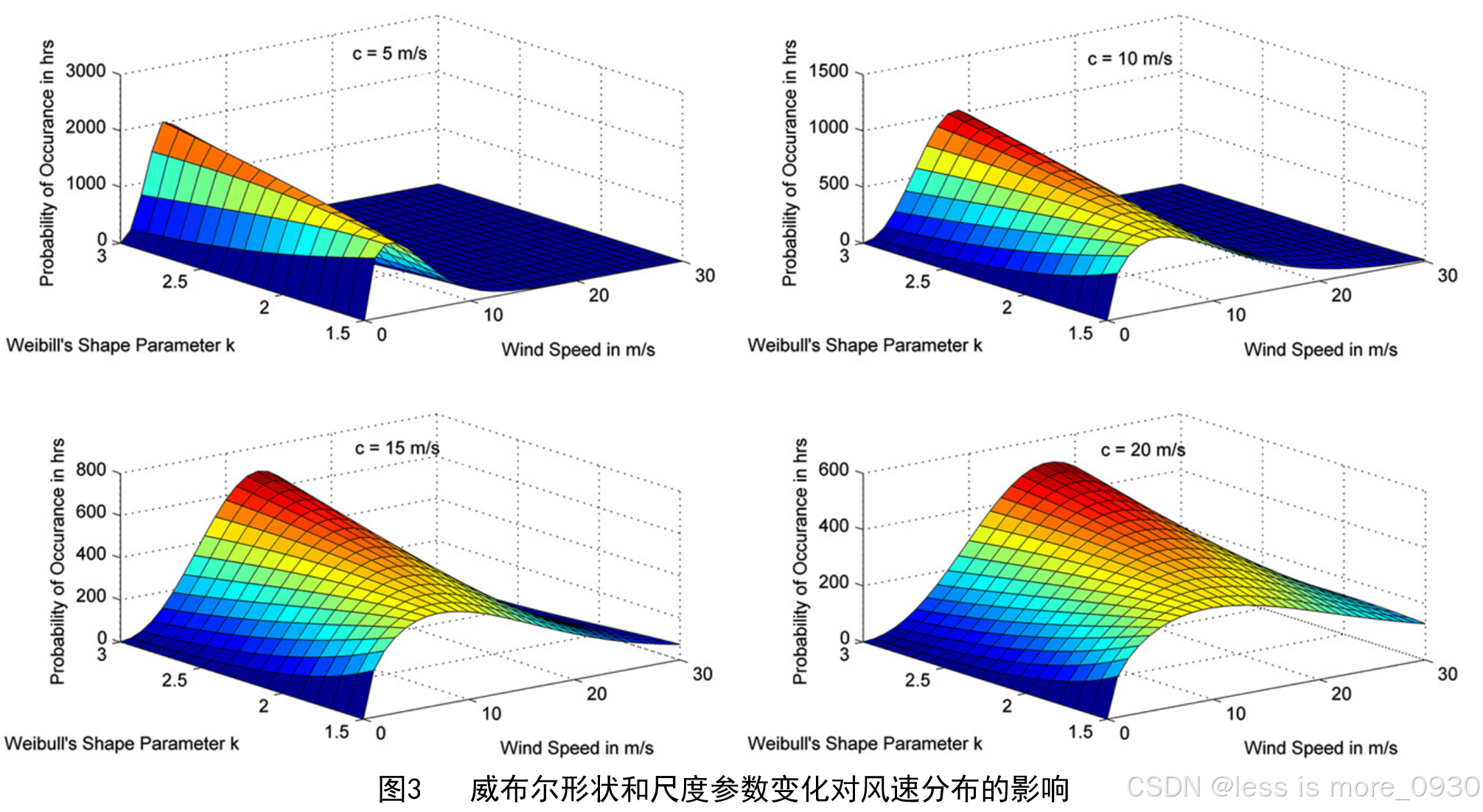
根据所选地点风廓线的不同,威布尔形状参数(k)和威布尔尺度参数(c)的值会发生变化。这些参数的变化对风速分布的影响如图3所示。从图中可以清楚地观察到,随着威布尔参数k 和 c 值的增加,风速分布向右移动,即向更高的风速移动, 意味着更高风速将持续更长的时间,使得能量输出更高[3]。
3.2 塔架高度和地形粗糙度对风能转换系统性能的影响
幂律[9-10],表达式为:就是在计算风功率时,选取的风速与高度有关。有许多复杂的公式被用来表示风速随高度的变化,但过于复杂,对一般的工程研究没有任何用处[4]。许多研究人员致力于寻找更简单的表达式,虽然它们在理论上可能不精确,但也会得到令人满意的结果。这些简单的表达式中最常见的

式中,v2 为换算得到的轮毂高度处的风速;v1 为风速计高度测得的风速;h2 为轮毂所处的高度;h1 为风速计所处的高度;a 为地面摩擦系数。
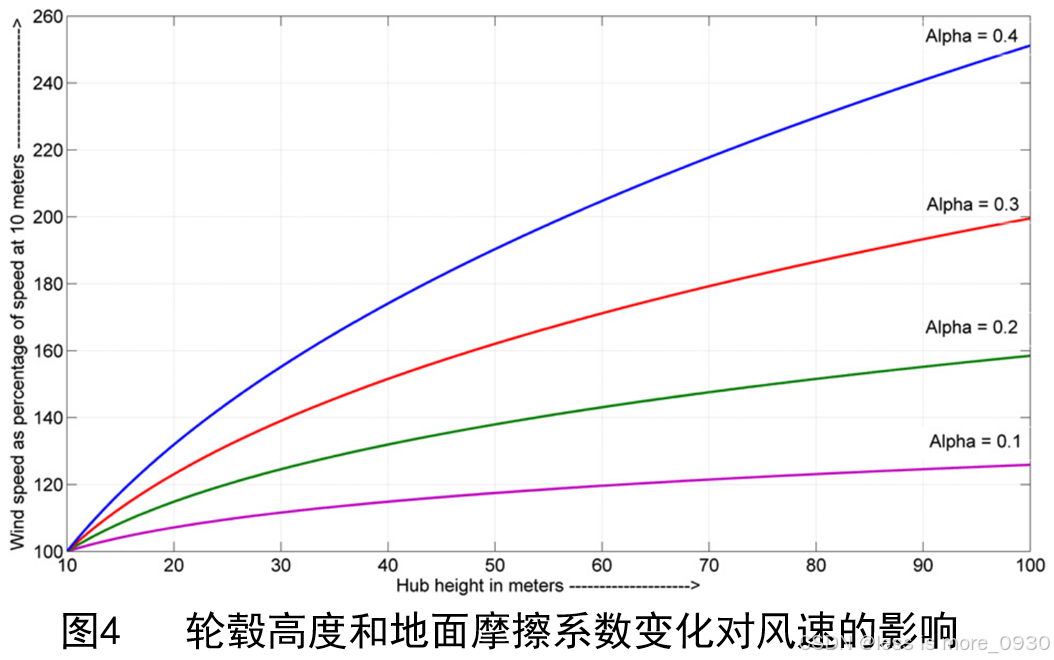
从式(8)中能发现,风速,即风机产生的输出能量,取决于风机所处的高度和地形的粗糙度。轮毂高度和地形粗糙度(以地面摩擦系数a 衡量)的影响如图4所示。从图4行看出,轮毂高度和地面摩擦系数对风速的影响较大。因此,为了使风机输出功率计算更加准确,必须将风速计高度测得的风速按式(8)换算为轮毂高度处的风速[3]。
3.3 风机功率曲线
给定风力发电机在特定风速下产生的电功率可以直接由制造商提供的风机功率曲线得到。由于风机的设计方式与额定值不同,使得风机的功率曲线形状不同。本质上,功率曲线由建造者进行认证,认证过程由“国际电工委员会”(IEC)建立。所谓的程序包括“同时测量”“风速”和“输出功率”,在“试验场”进行相当长时间的测量,目的是在不同的“大气条件”下收集信息,根据这些信息可以定义观察到的功率曲线。一般情况下,该曲线可通过“归一法”得到。风力机的理想功率曲线和特定的运行模式如图5所示[11]。
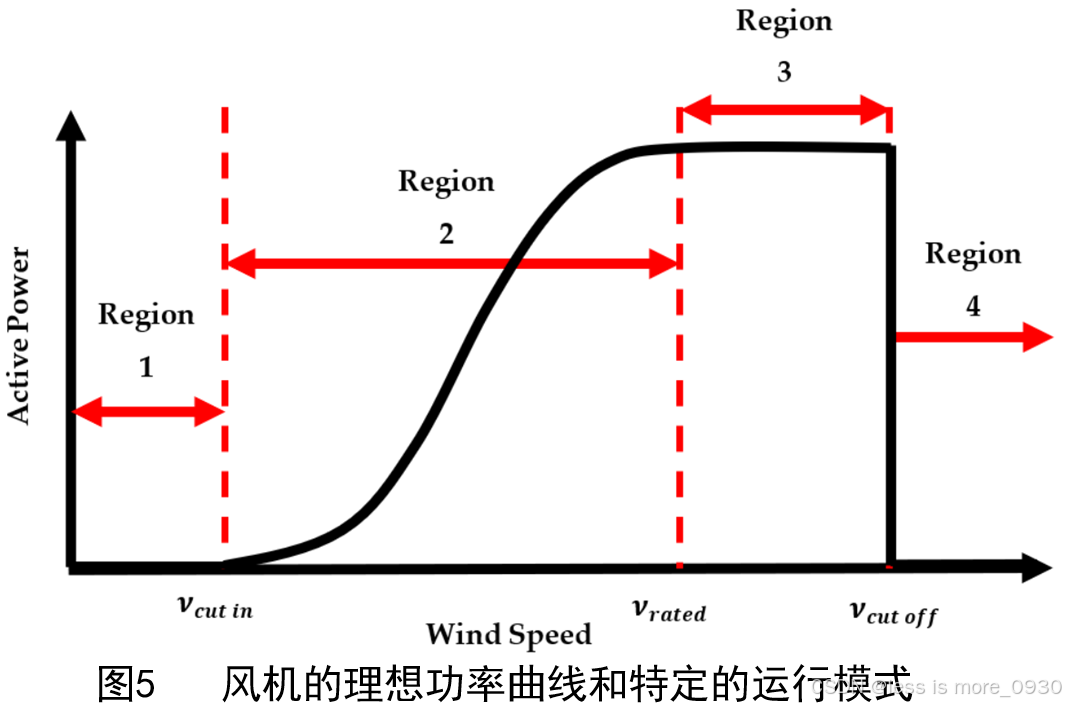
风力发电机输出功率模型首要包括风力发电机基础功率方程模型和风力发电机功率曲线模型,选择合适的风力发电机输出功率模型在发电平台的设计过程中至关重要[12]。
4 基本功率方程模型
式(1)即为由风能功率方程得到的风力发电机基本电功率方程,其中囊括密度ρa、风轮扫过的面积A、轮毂处风速v 三个参数。
风机风轮扫过的截面积A 为:
![]()
式中,D为风轮的直径。
风力发电机安装地的空气密度是影响风力发电机输出功率的一个重要因素,通常情况下,当无法获得风机安装地的大气压和空气温度时,就会采用恒定的空气密度来计算输出功率。当温度为15℃,大气压为 1013 兆帕时,采用恒定空气密度的计算方法是有效的。但空气密度一般与当地的大气压力、环境温度和海拔高度等因素有关,因此使用恒定值会在电力系统的设计中引入一个能源输入误差,导致系统的性能下降。修正后的空气密度ρa 的表达式为[13]:
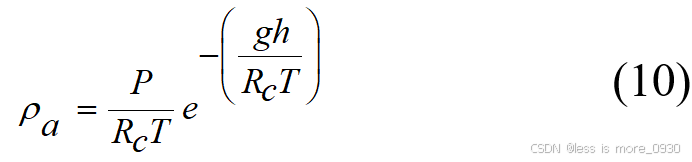
式中,P 为大气压力;Rc 为摩尔气体常量,287.05 J/(K·mol);T 为环境温度;g 为重力加速度;h 为海拔高度。
风能利用系数Cp 与桨距角 b 和叶尖速比 l 有关,其表达式为[14]:
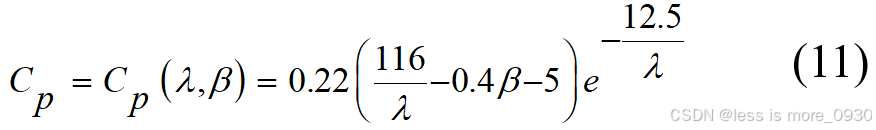
将风力发电机主要电功率方程中各参数的具体表达式代入,可得风力发电机输出功率为:
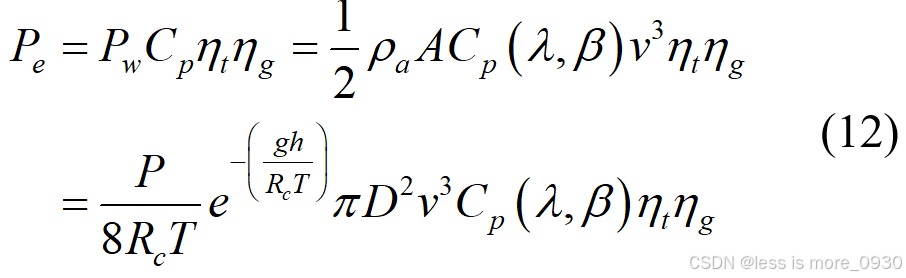
典型风力发电机的输出功率曲线如图5所示。典型的风力发电机输出功率模型核心考虑以下三个方面:(1)空气密度随天气的变化;(2)不同风速范围内的功率模型;(3)风能利用系数的变化。典型风力发电机的输出功率模型为[12]:
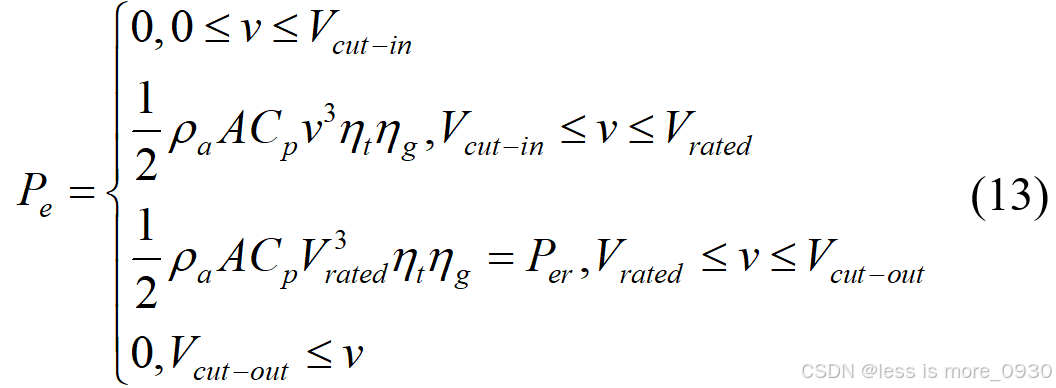
4.1 风力发电机功率曲线模型
通常使用风力发电机的功率曲线作为其功率模型,而功率曲线的获得主要有两种方法:(1)用假定的功率曲线模型;(2)用风力发电机制造商提供的实际功率曲线模型[3]。
4.1.1 假定的功率曲线模型
风力发电机的假定功率曲线模型主要包括线性模型、二次方模型、三次方模型、威布尔参数模型和指数模型等,这些模型均根据风机启动风速和额定风速两点处的风速和功率进行拟合得到。
(1)线性模型
Yang等人[15]和Abouzaher等人[16]提出了一种非常简单的风电机组性能预测模型。他们假设风速处于启动风速到额定风速这一阶段内,风力机的输出功率随风速的增加而线性增加,随后从额定风速到切除风速这一阶段内的输出功率保持不变。据此,提出了风力机功率输出模型为[3]:
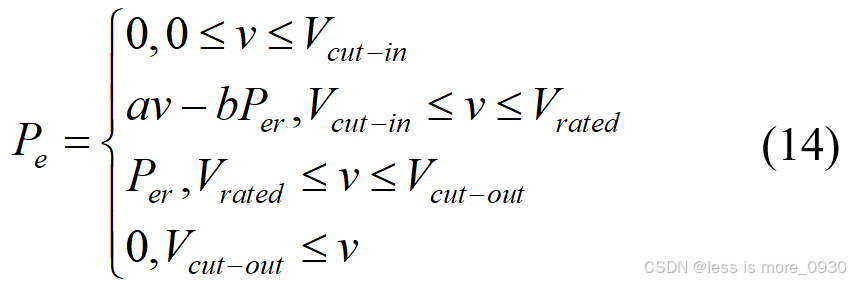
式中,系数 a 和 b 的表达式由风机启动风速和额定风速两点处的风速和功率利用两点式公式进行求解:
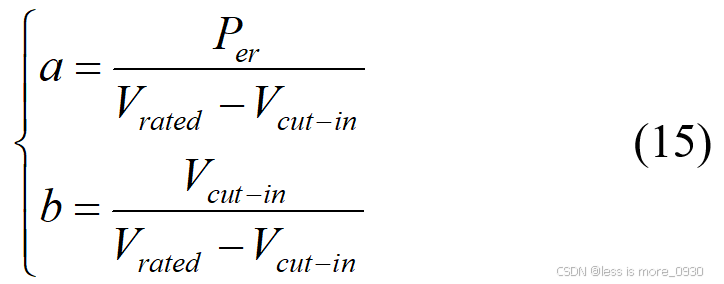
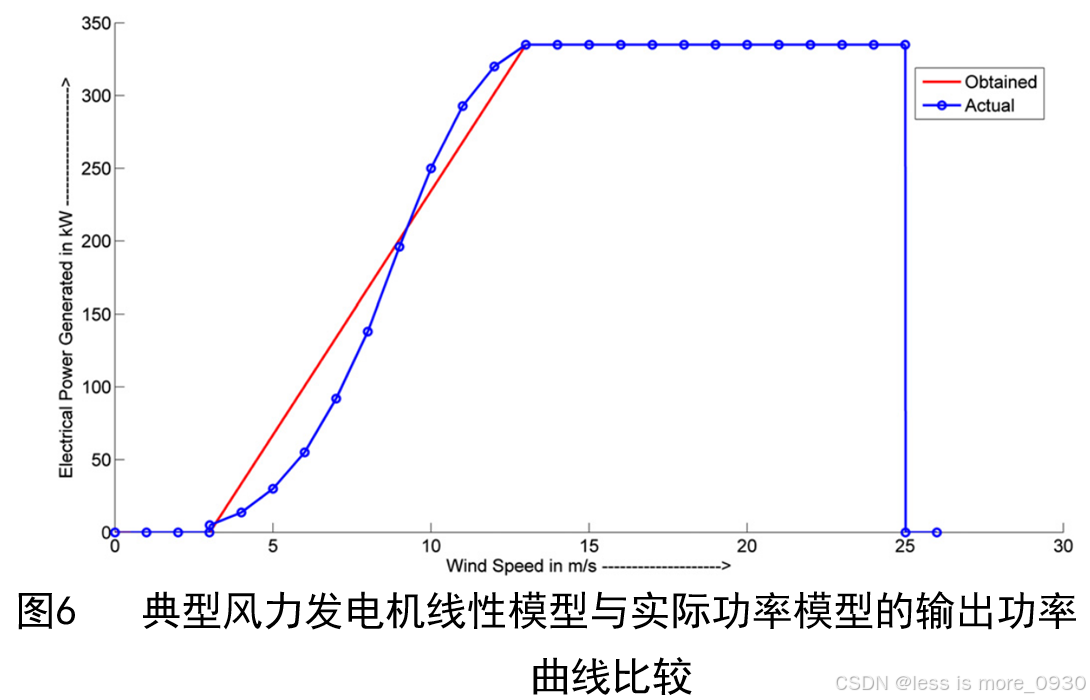
该风力发电机采用线性模型得到的输出功率曲线与实际输出功率曲线比较如图6所示,从图中可以看出线性模型得到的功率曲线存在一定的偏差,是一种近似的途径,得到的解不够精确,因此通常使用的较少[3]。
(2)二次方模型
典型风力发电机的输出功率采用二次方模型,其功率输出模型主要有两种,第一种二次功率模型为[12]:
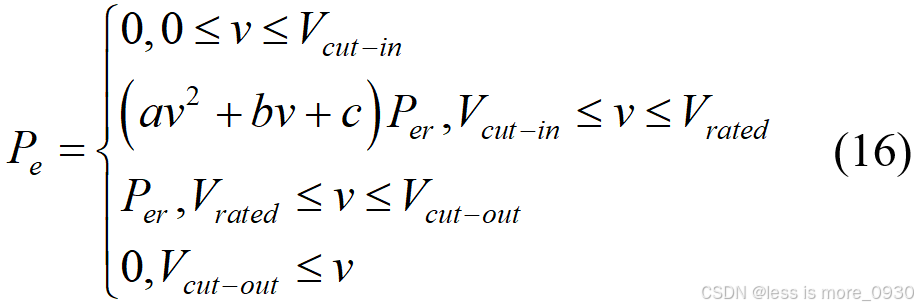
当 Vcut-in≤v≤Vrated时,二次功率方程的系数a、b和 c 由下式决定:
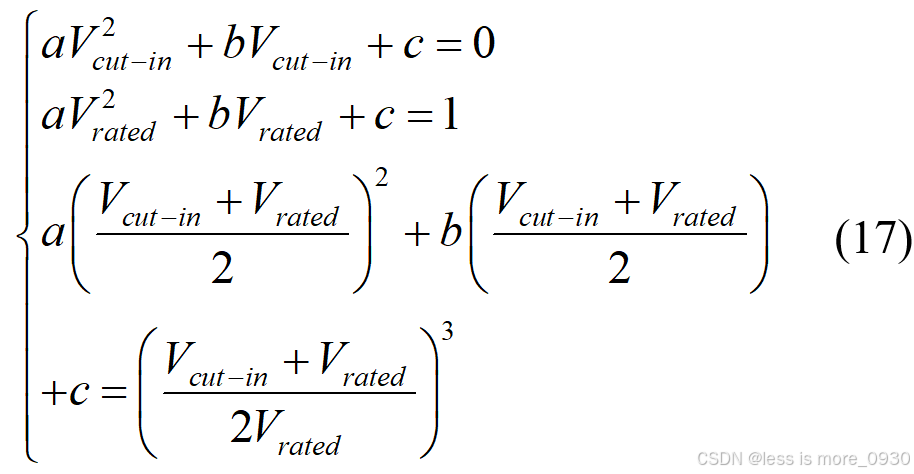
求解三个系数可得:
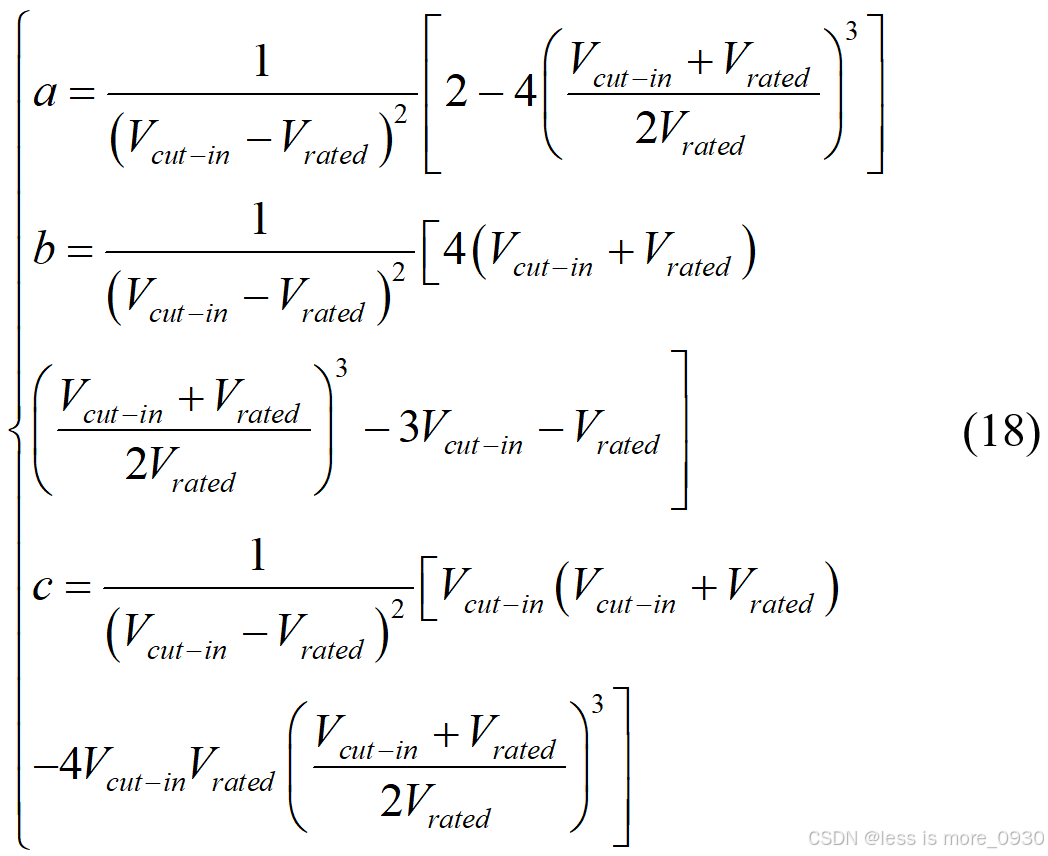
第二种二次功率模型为[12]:
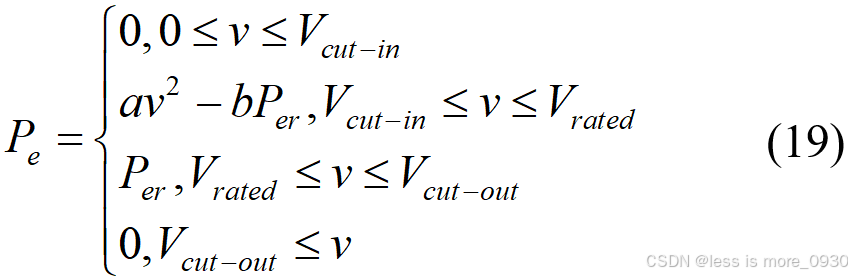
式中,系数 a 和 b 的表达式由风机启动风速和额定风速两点处的风速和功率代入Vcut-in≤v≤Vrated时的公式进行求解:
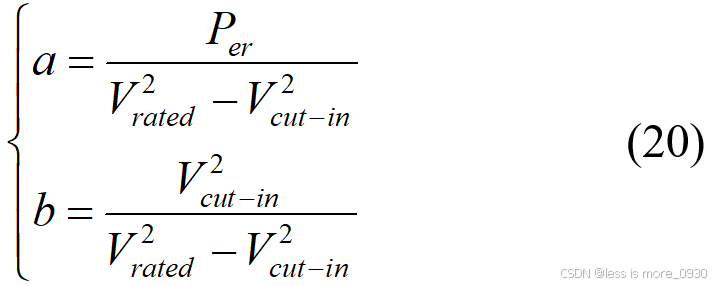
在实际应用中仍无法较好的表征风力发电机实际输出功率,因此采用的也较少。就是二次方模型相比于线性模型,其对呀风力发电机输出功率拟合的效果有所提升,但
(3)三次方模型
风力发电机的输出功率也可以采用三次方模型进行拟合,其功率输出模型主要有两种。第一种三次方模型由Deshmukh等[17]和Chedidd等[18]提出,其功率计算表达式为:
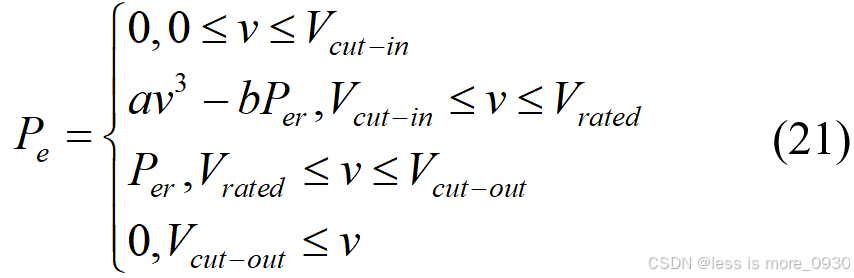
式中,系数 a 和 b 的表达式由风机启动风速和额定风速两点处的风速和功率代入Vcut-in≤v≤Vrated时的公式进行求解:
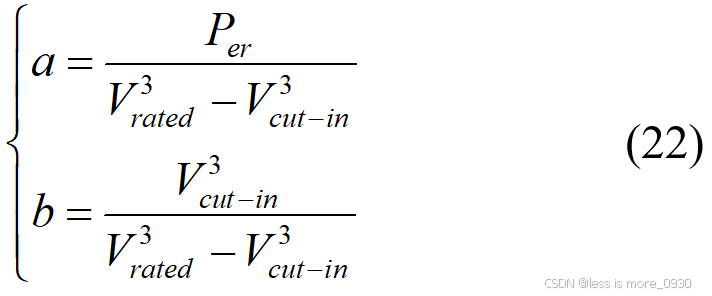
第二种三次方功率模型为[12]:
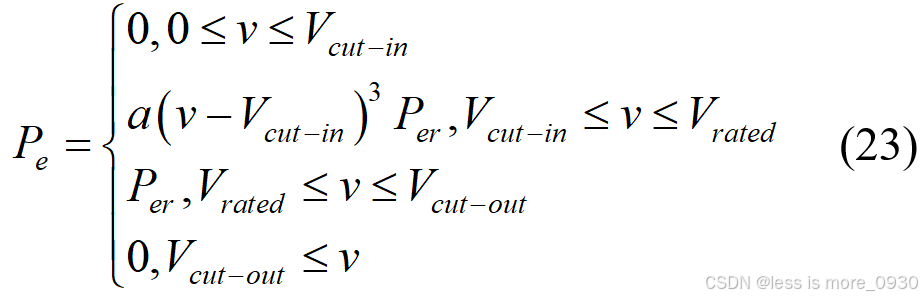
式中,系数 a 和 b 的表达式由风机启动风速和额定风速两点处的风速和功率代入Vcut-in≤v≤Vrated时的公式进行求解:
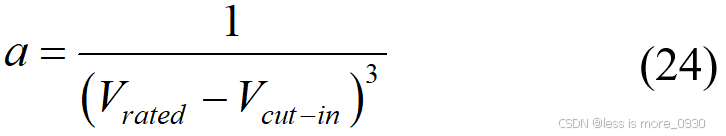
(4)威布尔参数模型
风力发电机的输出功率采用威布尔参数模型,其功率输出模型为[3]:
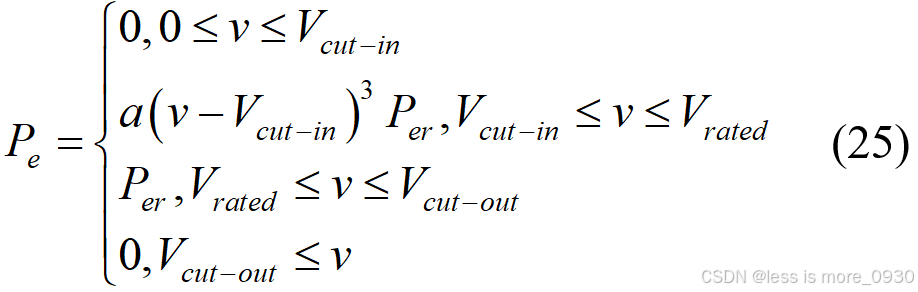
式中,系数 a 和 b 的表达式由风机启动风速和额定风速两点处的风速和功率代入Vcut-in≤v≤Vrated时的公式进行求解:
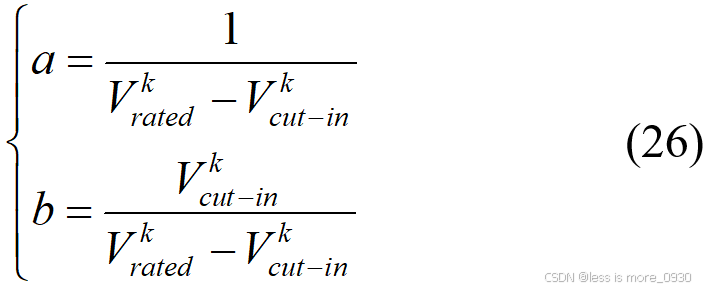
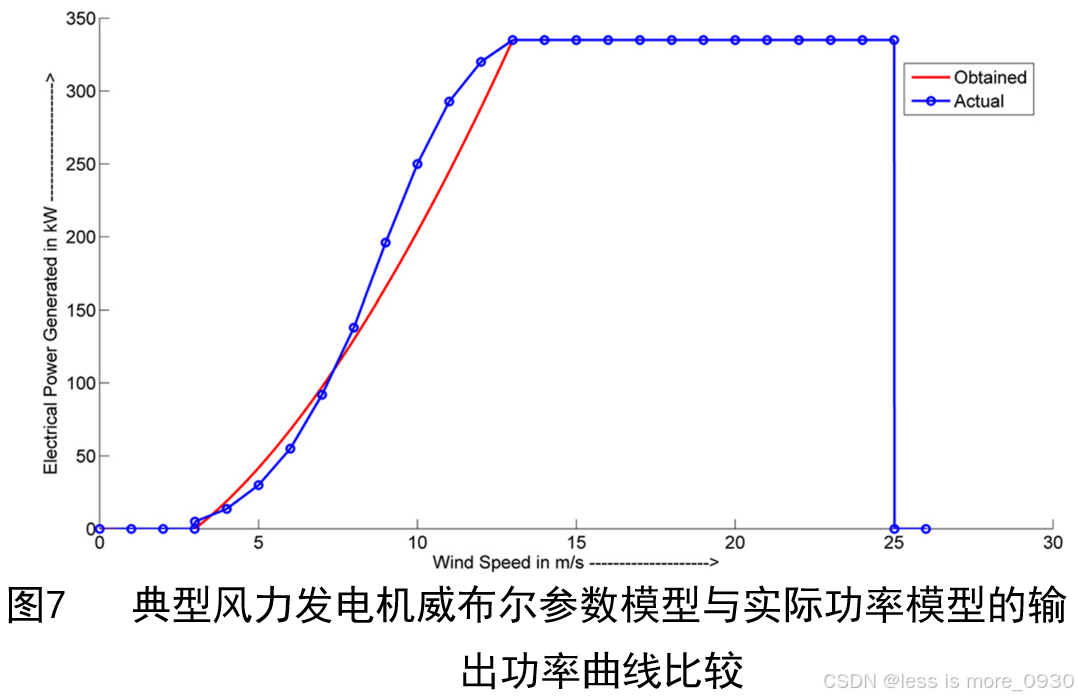
从图6和图7许可看出基于假定功率曲线的模型都是一些简化的模型,具有一定的可靠性,但是这些模型并没有准确的表示真实功率情况,依然存在一些误差。
4.1.2 实际的功率曲线模型
风力发电机的实际功率曲线模型能够凭借最小二乘法和三次样条插值技术等办法得到。
(1)最小二乘法
Ai等[19]利用最小二乘法拟合风力机的实际功率曲线,建立了风力机的特性方程。为了保证较好的拟合精度,至少启用了3个二次表达式。据此,提出了以下基于最小二乘法的方程来预测风力机的输出功率:
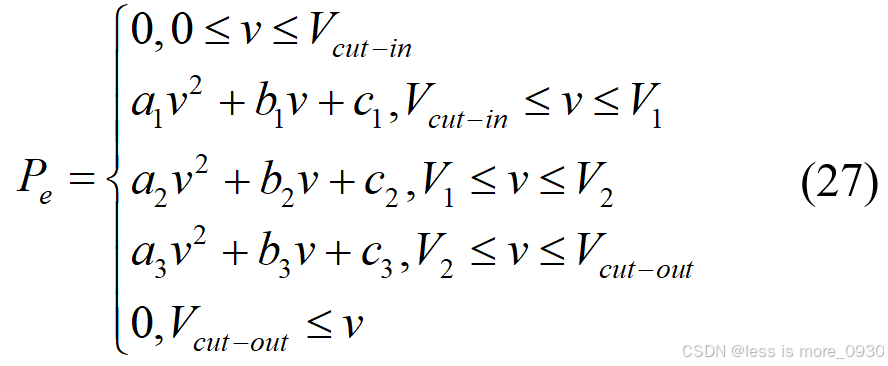
其中 ai、bi、ci(i=1,2,3)为二次方程的系数。
通过基于上述方法,能够得到描述所选风力发电机的方程。由艾纳康公司生产的模型号为 E-33 的风机,其基于最小二乘法的拟合功率曲线为[3]:
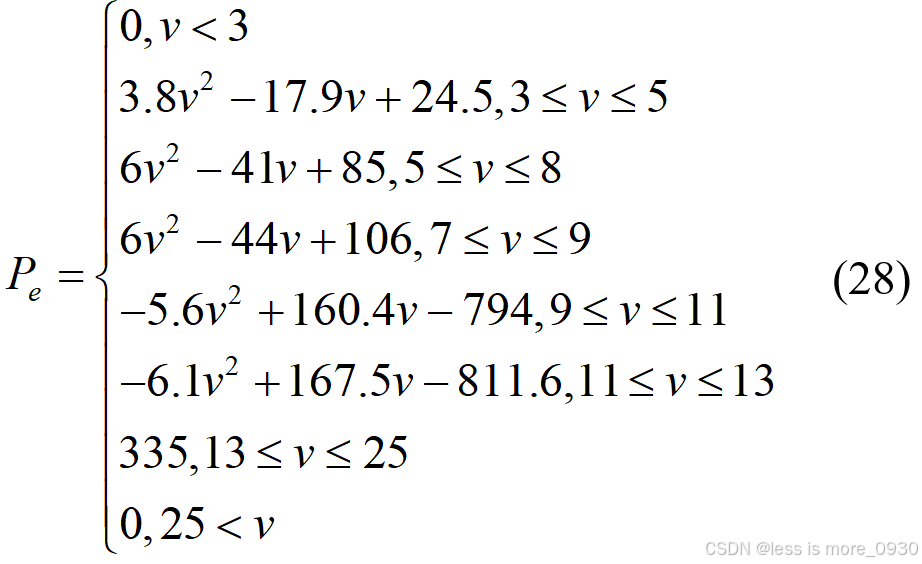
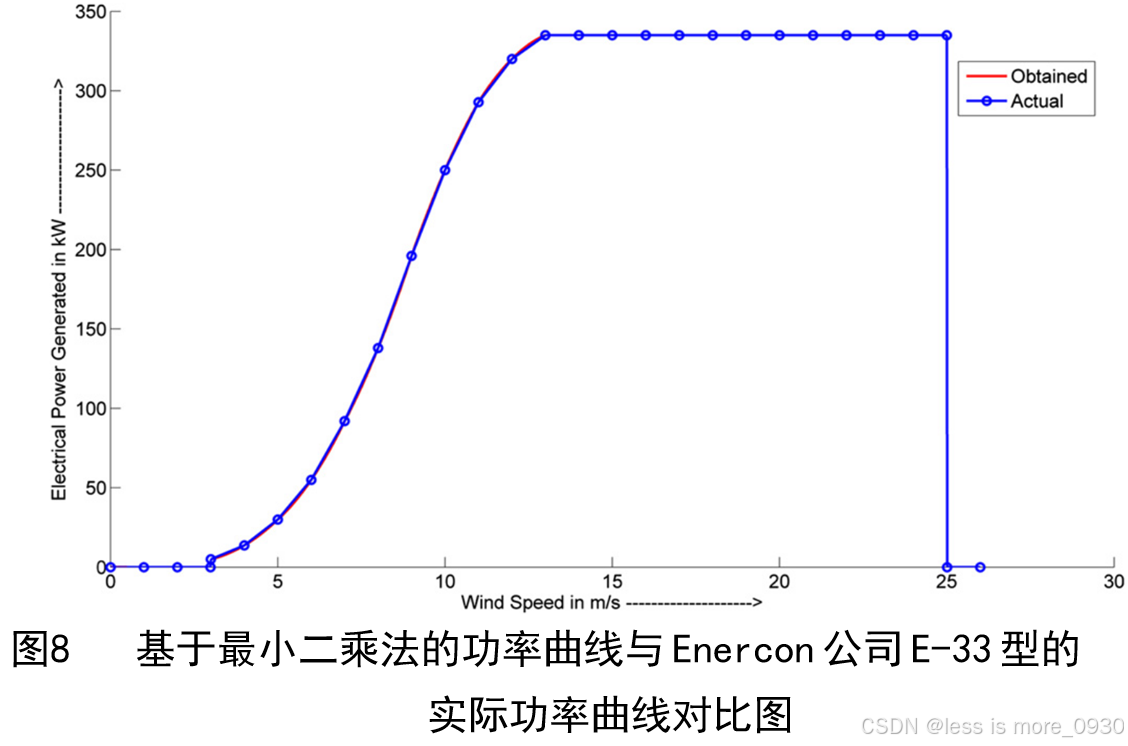
通过拟合功率曲线与厂家给予的功率曲线对比如图8所示。能够观察到,这两条功率曲线完全吻合。
(2)三次样条插值
三次样条插值是分段三次多项式插值,它在整个插值区间具有一阶和二阶导数,使曲线具有较好的光滑程度和插值精度,它具有转折自如的灵活性和计算的稳定性。Diafd等[10]和Hocaoglu[20]采用三次样条插值法对厂家提供的数据值进行拟合,计算出风力机的输出功率。据此,风电机组功率曲线拟合方程可表示为:
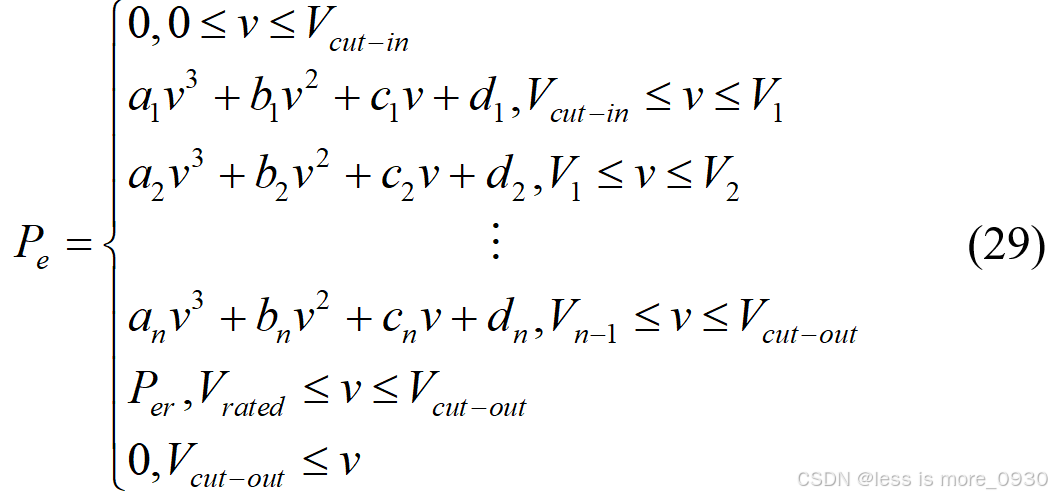
式中,n 为 n+1 个风速值与功率对应的三次样条插值函数的个数;ai、bi、ci、di (i=1,2,3,…,n)等为三次样条插值函数的多项式系数,取决于所选风力机的功率曲线。
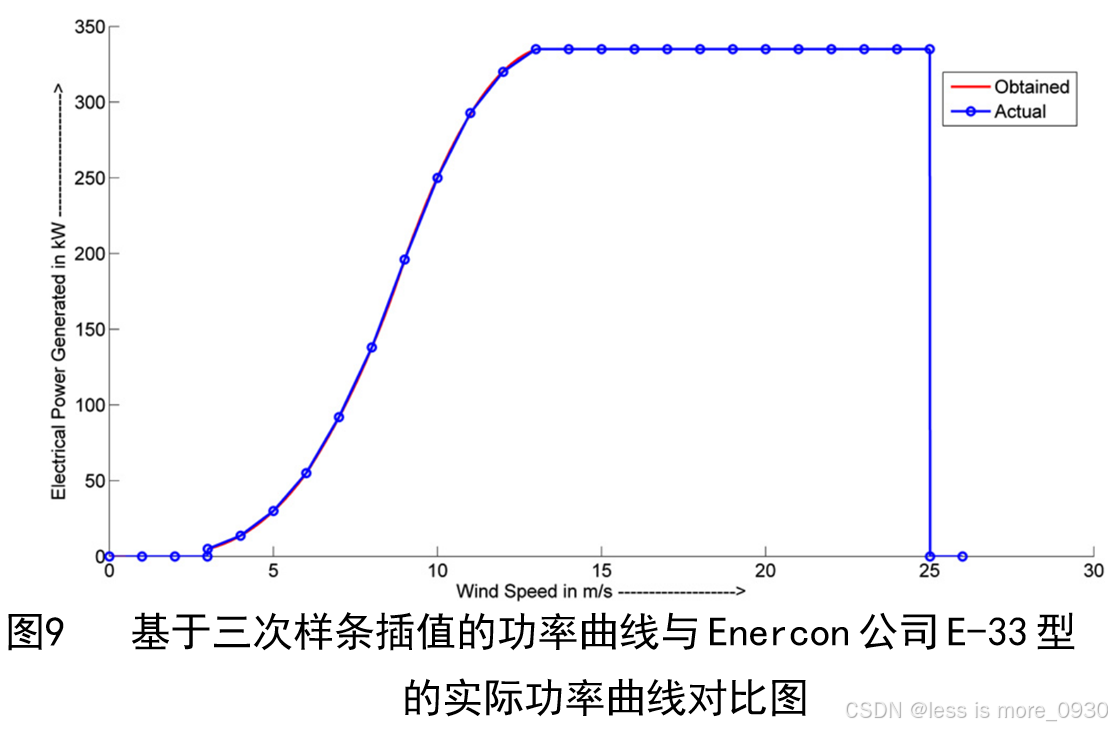
基于上述技巧,可以得到描述所选风力发电机的方程。模型号为 E-33 的风机由 Enercon Ltd 生产,其拟合功率曲线为:
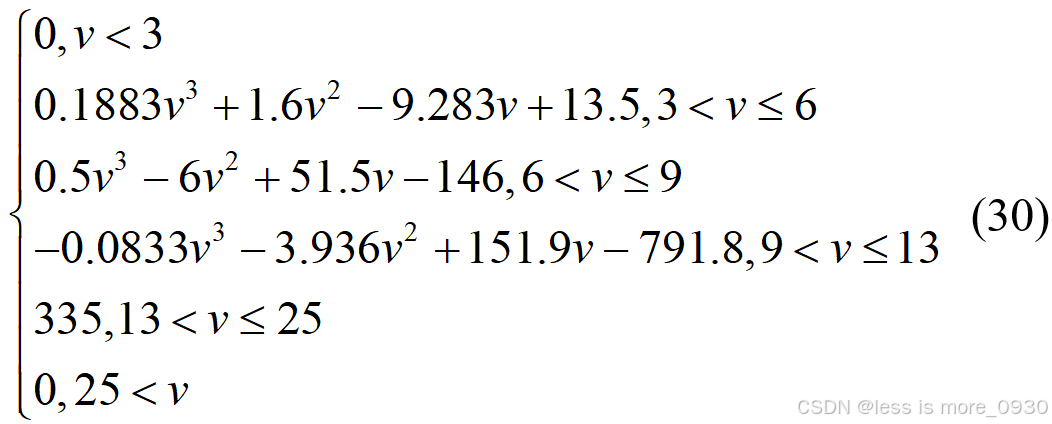
拟合功率曲线与厂家提供的功率曲线对比如图9所示。可以观察到,这两条功率曲线完全吻合[3]。
5 结论
风力发电机的输出功率模型包括两大类:(1)基本功率方程模型和(2)功率曲线模型。其中,风力发电机功率曲线模型又包括两种:(1)假定的功率曲线模型和(2)实际的功率曲线模型。从拟合的结果不难看出,假定的功率曲线模型是经过简化的模型,就算具有一定的可靠性,但这些模型并没有准确的表示风力发电机的真实功率情况,而风力发电机的实际功率曲线模型能够真实可靠的反应其功率大小,对于风力发电环境或风光混合发电系统的优化设计提供理论指导。
参考文献
- 高培淇.考虑风铝联合参与框架频率控制研究[D].昆明理工大学, 2023.
- 人民日报. 新能源发电装机规模首超煤电 并网太阳能发电装机容量达7.1亿千瓦[EB/OL].https://www.gov.cn/yaowen/liebiao/202407/content_6964172.htm.
- THAPAR V, AGNIHOTRI G, SETHI V K. Critical analysis of methods for mathematical modelling of wind turbines [J]. Renewable Energy, 2011, 36(11): 3166-3177.
- Johnson GL. Wind energy systems. Electronic Edition. Manhattan KS; 2001.
- Shanta AS, Hanitsch R. Evaluation of wind energy potential and electricity generation on the coast of Mediterranean see in Egypt. Renew Energy 2006; 31:1183e202.
- Bagiorgas HS, Assimakopoulos MN, Theoharopoulos D, Matthopoulos D, Mihalakakou GK. Electricity generation using wind energy conversion systems in the area of Western Greece. Energy Convers Manage 2007;48:1640e55.
- Patel MR. Wind and solar power systems e design, analysis, and operation. 2nd ed. New York: CRC Press; 2006.
- Lu L, Yang H, Burnett J. Investigation on wind power potential on Hong Kong Islands e an analysis of wind power and wind turbine characteristics. Renew Energy 2002;27:1e12.
- Wang C, Nehrir MH. Power management of a stand alone wind/ photovoltaic/fuel cell energy system. IEEE Trans Energy Convers 2008;23(3):957e67.
- Diaf S, Diaf B, Belhamel M, Haddadi M, Louche A. A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 2007;35:5708e18.
- Bilendo Francisco, Meyer Angela, et al. Applications and Modeling Techniques of Wind Turbine Power Curve for Wind Farms—A Review. Energies (Basel) 16.1 (2023): 180.
- 李冲,郑源,朱大胜,等.风力发电机输出功率模型研究[J].水力发电,2014,40(08):123-125+128.
- OLAOFE Z O, FOLLY K A. Wind energy analysis based on turbine and developed site power curves: A case -study of Darling City [J]. Renewable Energy, 2013, 53: 306-318.
- 杨培宏,胡庆林,付盼,等.考虑风能利用系数的风电场等值建模[J].中国科技论文,2016,11(23):2711-2715.
- Hongxing Y, Wei Z, Chengzhi L. Optimal design and techno-economic analysis of a hybrid solarewind power generation system. Appl Energy 2009;86: 163e9.
- Abouzahr I, Ramakumar R. An approach to access the performance of utility - interactive wind electric conversion systems. IEEE Trans Energy Convers 1991; 6(4): 627e38.
- Deshmukh MK, Deshmukh SS. Modelling of hybrid renewable systems. Renew Sustain Energy Rev 2008; 12(1): 235e49.
- Chedid R, Akiki H, Rahman S. A decision support technique for the design of hybrid solarewind power systems. IEEE Trans Energy Convers 1998; 13(1): 76e83.
- Ai B, Yang H, Shen H, Liao X. Computer-aided design of PV/wind hybrid system. Renew Energy 2003; 28: 1491e512.
- Hocaoglu FO, Gerek ON, Kurban M. A novel hybrid (wind-photovoltaic) system sizing procedure. Solar Energy 2009;83:2019e28.
