威尔逊定理: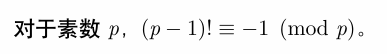
首先,对于 \(p = 2\),显然成立。
若 \(p \not= 2\),我们考虑一个 \(x\) 在模 \(p\) 意义下的逆元若是他自己,则 \(x^2\equiv 1(\text{mod}\ p)\)。
\(x\equiv 1\) 或 \(p - 1(\text{mod}\ p)\)。
而且已知,若 \(a_i \in \{2, \dots, p - 2\}\) 不相同,则 \(a_i^{-1}\in \{2, \dots, p - 2\}\) 也不相同。
并且,因为 \(p\) 为奇数,所以集合 \(\{2\dots,p - 2\}\) 的大小为 \(p - 2 - 2 + 1 = p - 3\),为偶数。
因此,我们可以让 \(2\dots, p - 2\) 两两配对,构成几组互逆的元素。
因此 \((p - 1)! \equiv 1\cdot (2\cdot 3\dots (p - 2)) \cdot (p - 1) \equiv 1\times 1\times (-1) \equiv -1(\text{mod}\ p)\)
