前置知识:倍增
其实倍增就是二进制拆分,因为有的数可能很大,我们按照2的幂次去查询,就能用 \(log_2n\) 的时间复杂度求解
ST 表
创建
ST 表运用的是倍增思想,我们可以用 \(O(nlogn)\) 的时间创建一个二维表,根据倍增思想就可以实现 \(O(1)\) 的区间最值查询(RMQ 查询)
我们这样定义:
定义 \(dp[i,j]\) 表示 \([i,i+2^j-1]\) 区间的最值,易得这个区间的长度为 $ 2^j$ ,那么根据倍增,这个区间可以分成两个长度为 $ 2^{j-1} $ 的区间,使用递推求解,递推式如下(max 可换成 min):
\[dp[i,j]=\max(dp[i,j-1],dp[i+2^{j-1},j-1])
\]
那么我们可以得出模板代码:
void init_st(){int k=log2(n);for(int i=1;i<=n;i++){dp[i][0]=a[i];}for(int j=1;j<=k;j++){for(int i=1;i<=n-(1<<j)+1;i++){dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);}}
}
这里先枚举 \(k\) 是因为我们需要通过 \(k\) 来确定枚举的右区间,不然范围就会超过 \(n\)。
查询
我们要查询的是一个 \([l,r]\) 区间,我们可以这样理解一下:
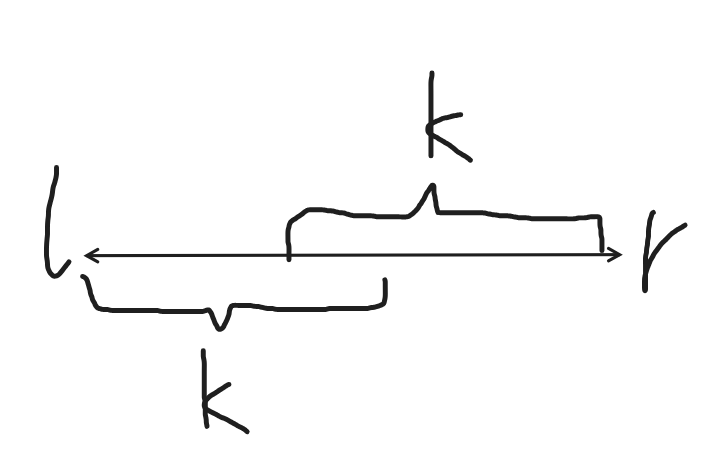
我们只要找到一个最大的不超过 \(l,r\) 长度的 2 的幂次 \(k\),就能用建好的 ST 表计算答案。
而根据对数的定义:
\[\log_2n=a \to 2^a=n
\]
所以,我们有($ [l,r]$ 表示 \(l,r\) 这个区间的长度):
\[\log_2[l,r]=k\to 2^k=[l,r]
\]
所以 \(k\) 的答案是\(\log_2 r-l+1\),其中 \(r-l+1\) 求的是区间 \([l,r]\) 的长度。
那么就能够得出查询的公式:
\[k=\log_2r-l+1\\
ans=\max(dp[l][k],dp[r-2^k+1][k])
\]
所以代码就很好写:
int k=__lg(y-x+1);
cout<<max(dp[x][k],dp[y-(1<<k)+1][k])<<endl;
总结
ST 表是基于倍增思想完成的一种支持 RMQ问题(静态区间最值问题查询)的数据结构
ST 表能够实现 \(O(n\log n)\) 建表
尝试独自完成洛谷 P3865 【模板】ST 表 & RMQ 问题
