DP优化
P2224 [HNOI2001] 产品加工
首先是暴力DP,社fi,j1,j2,第i个物品,A机器j1事件,B机器j2事件,然后直接转移就行了,但是n^3的状态,孬
考虑降维,bool的内容可以改为数值,社fij表示第i个任务,A机器做了j时间B机器的最小时间,可以转移了

空间炸就滚动数组,但是时间会炸。
但是我们发现状态是递增的,可以将枚举上界改为记录上界,小于下界的都可以不用管了,每次上界最多更新就是max(t1,t3)
CF1870E Another MEX Problem
给你一个序列 a,让你选出一些不交的子串,使得它们的 MEX 的异或和最大。
有一个套路是异或记录可行性,而不是最优化,题解说的。
社fij表示上一个右端点位置小于i时,答案是否可以是j,直接枚举转移点转移即可,但是MEX不好算,复杂度是n^3的,要O(n)转移
但是我们发现有效的转移点区间极少,可以记录这些有效转移点,只从它们转移

P3188 [HNOI2007] 梦幻岛宝珠
就是那种一道橙题使劲加数据范围然后甩你几个性质让你做的。
考虑从大到小枚举b
设 fi,j 为 选了j∗2^i 重量的最大价值, 实际上 2^i 以下的重量被忽略了。
考虑转移,同为 2^i 重量的物品间可以相互转移: 当前是第x个数:
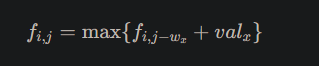

类似一个背包套背包。
luogu模拟赛
T1
直接map维护出现次数和偏移即可
T2
首先分讨,发现钦定了一个节点为A1之后,后面的的点必须选与他同深度的,浅了显然不合法,深了你永远取不到交集。
预处理mxdepi表示i子树最大深度。
发现选的所有点mxdepi最小值一定是mxdepA1,最大值不限。
然后就是一个排列数了,随便你怎么计数就行
T3
树套树二分3log(bushi)
考虑线段树,维护ji表示点i的最小可达右端点,修改就是重置一个区间的最小可达右端点。
然后维护查询,考虑查询x,t,可选右端点就是max(y, j_i),代价就是p_{max(y,j_i)} - p_i。
分类讨论
若 j_i < y,代价为 p_y - p_i,该类的最优是 p_y - max(p_i)(在满足 j_i<y 的 i 中取 p_i 的最大值)。
若 j_i >= y,代价为 p_{j_i} - p_i,该类的最优是在满足 j_i>=y 的 i 中取 min(p_{j_i} - p_i)
我们直接维护maxji minji maxpi min(ji - pi),类似于吉斯基的东西,保证checkmin,checkmax均摊复杂度是log。
具体地,区间修改时,类型 1 事件 [x,y] 会把区间内的 j_i 更新为 max(j_i, y+1)(因为所有 (i, j) 且 x<=i<j<=y 被删掉)
对于查询,分讨后代价直接取能取到的右面最小值计算即可。

