3.\(AC\)自动机
前言
兴许是字典树上的树上的 \(kmp\) ? \(O(n \times |C|)\) \(C\) 是字符集的大小,跑起来回比 \(O(n)\) 慢, 但是 \(|C|\) 的部分常熟小就是了.
介绍
\(kmp\) 与字典树结合产物.\(kmp\) 只能处理单个模式串或者文本串, 而 \(AC\) 自动机可以处理多个模式串, \(AC\) 自动机的 \(fail\) 指针(失配指针)可以理解成在字典树上找一个前缀使得其能与当前状态匹配最长的后缀.如果我们只插入一条模式串,不难发现这就是 \(kmp\) 跳 \(border\) 的过程.
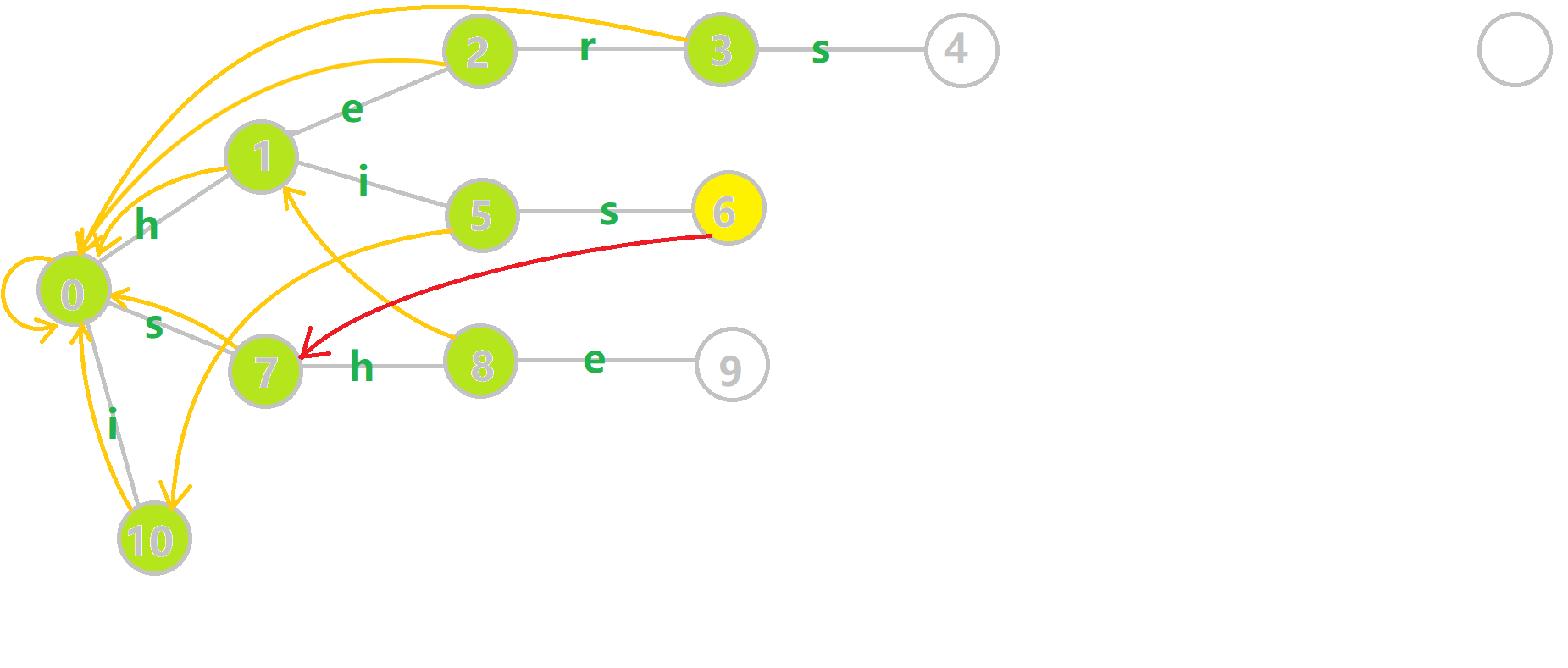
图片来自 \(oi\) \(wiki\)
实现
\(fail\) 指针构建
约定
- 首先考虑只有一个模式串的情况,这个 \(fail\) 指针不能指向自己.
- 对于一个没有被修改过的用于指向子节点的指针可以看做指向 \(Null\) 节点, 根节点是 \(1\) 号节点.
- \(Null\) 节点约定为 \(0\) 号节点
构建
- 考虑广搜构建
- 当前节点编号为 \(i\) 的子节点的 \(fail\) 指针应该指向当前节点的 \(fail\) 指针指向的节点的编号为 \(i\) 的子节点的 \(fail\) 指针,有几种情况,为了方便我们将当前节点编号为 \(i\) 的子节点的叫做 \(to\), 当前节点的 \(fail\) 指针指向的节点的编号为 \(i\) 的子节点的 \(fail\) 指针叫做 \(nxtfail\)
-
两个子节点都存在,只要 \(to\) 的 \(fail\) 赋值为 \(nxtfail\) 就可以了
-
\(nxtfail\) 不存在, 此时 \(nxtfail\) 指向 \(Null\) 节点,而 \(Null\) 的子节点的指针又指向 \(Null\),我们只需让 \(Null\) 的子节点的指向 \(root\) 节点就可以, 正确性显然,相当于失配后又从根节点开始
-
\(to\) 不存在直接将 \(to\) 赋值为 \(nxtfail\) 就可以了相当于跳 \(fail\)
-
对于 \(1,2\) 情况的 \(to\) 应该入队, \(3\) 情况由于节点不存在不应当入队
-
(推荐左值引用的写法)
-
- 不难发现 \(fail\) 指针会构成一棵树,因为 \(fail\) 指针指向的节点的深度一定更低.
【模板】AC 自动机
一个多模式串匹配单个文本串,考虑一个朴素的方法, 我们在字典树上"插入"文本串, 如果下一个节点空了就跳 \(fail\) , 由于我们已经处理了使得所有空的子节点都指向了 \(fail\), 插入时按照正常的方法插入就好了.对于 \(s\) 经过得每个节点 \(cnt++\), 代表一个方案数.考虑只有一个模式串时,不难发现上面的过程相当于 \(kmp\) ,最后的节点的方案数就是我们所要的方案数.多个模式串时由于某个的模式串可能包含其他模式串, 这时我们将 \(fail\) 的入度为零的节点的方案数向上加, 然后更新 \(fail\) 的入度.不难发现上述方法就是个拓扑.询问某个模式串的出现的个数,访问其在字典树上最后一个节点的 \(cnt\) 即可.
#include<bits/stdc++.h>
#define rep(i, l, r) for(ll i=(l);i<=(r);i++)
using namespace std;
typedef long long ll;const ll N = 2e5 + 10, M = 2e6 + 10;
ll n, m;
namespace AC {ll root, node_cnt;struct node {ll son[26], fail, ru, ans, bl;inline ll& operator[](ll x) { return son[x]; }}tr[N];ll Map[N], bl_cnt;inline ll newnode(){return ++node_cnt;}inline ll newbl(){return ++bl_cnt;}inline void init(){node_cnt = 0, root = newnode();}inline void ins(const char *s, const ll id) {ll len = strlen(s + 1);ll x = root;for (ll i = 1; i <= len; i++) {ll son = s[i] - 'a';if (tr[x][son] == 0)tr[x][son] = newnode();x = tr[x][son];}if (tr[x].bl == 0) tr[x].bl = newbl();Map[id] = tr[x].bl;}inline void build_Fail() {queue<ll> q;for (ll i = 0; i < 26; i++) tr[0][i] = root;q.emplace(root);while (!q.empty()) {ll x = q.front();q.pop();for (ll i = 0 ; i < 26; i++) {ll &to = tr[x][i];ll nxtfail = tr[tr[x].fail][i];if (to) {tr[to].fail = nxtfail;tr[nxtfail].ru++;q.emplace(to);}else to = nxtfail;}}}inline void query(const char *s) {ll len = strlen(s + 1);ll x = root;for (ll i = 1; i <= len; i++) {x = tr[x][s[i] - 'a'];tr[x].ans++;}}ll ans[N];inline void topu() {queue<ll> q;for (ll i = 1; i <= node_cnt; i++) if (tr[i].ru == 0) q.emplace(i);while (!q.empty()) {ll x = q.front(), fail = tr[x].fail;q.pop();ans[tr[x].bl] = tr[x].ans;tr[fail].ans += tr[x].ans;if (--tr[fail].ru == 0) q.emplace(fail);}}inline void Answer() {for (ll i = 1; i <= n ; i++) {cout << ans[Map[i]] << endl;}}
}
char s[M];
bool Memory_end;int main() {AC::init();scanf("%lld", &n);rep(i, 1, n) {scanf("%s", s + 1);AC::ins(s, i);}AC::build_Fail();scanf("%s", s + 1);AC::query(s);AC::topu();AC::Answer();return 0;
}
