此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第二周,在2.1之前的的基础补充。
本周的课程以逻辑回归为例详细介绍了神经网络的运行,传播等过程,其中涉及大量机器学习的基础知识和部分数学原理,如没有一定的相关基础,理解会较为困难。
因为,笔记并不直接复述视频原理,而是从基础开始,尽可能地创造一个较为丝滑的理解过程。
1.回归
1.1什么是回归?
首先依旧摆一个定义:
回归(Regression)是统计学和机器学习中的一种方法,用于建立自变量(输入特征)与因变量(输出目标)之间的关系。回归的目的是通过分析数据,找出输入与输出之间的函数关系,并且根据这个关系来预测连续型的输出值,回归模型的主要目标是预测连续变量。
简单来说,回归就是通过数据得到输入输出间的关系,再根据这个关系为输入预测连续型的输出。
之前在第一周中提到的用数据预测房价,就是回归问题。
之所以一直在强调输出的连续型,是为了和另一类问题:分类问题作区分,我们会在之后再展开,总之,回归问题得到的最终结果一定是一个连续的数值,如价格,身高,重量等,而非一类标签,如是或否等。
1.2 怎么回归?
我们现在知道了回归实现的效果,那如何实现回归呢?即输入输出的关系怎么得到的?
简单来说,就是通过输入输出得到拟合函数:
拟合函数可以是线性函数,多项式函数,分段函数等等,我们先忽略语境举一个最简单的例子:
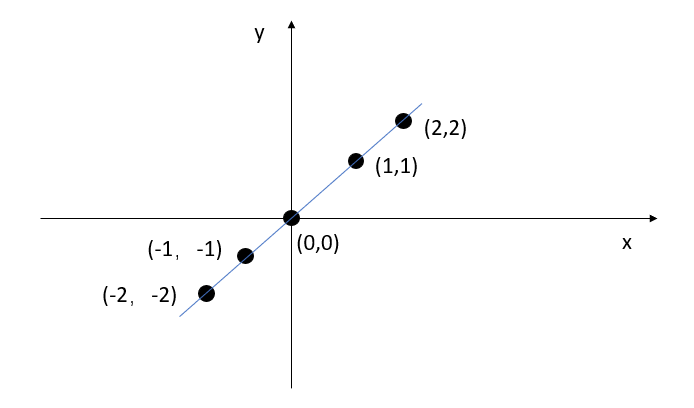
如图所示,假设我们的数据即为图中点,我们观察数据,直接得到拟合关系:
我们通过把输入代入拟合函数,即可预测其他输入的输出:输入5,输出5;输入1.2得到1.2.
1.3 线性回归
线性回归可以说是最简单的回归算法,刚刚的 \(y=x\) 就是最简单的线性回归,线性回归得到的拟合函数图像一定是一条直线。
线性回归的通式如下:
其中,在数学上,\(w\) 被称为斜率,\(b\) 被称为截距。
但在机器学习与神经网络的背景下,二者通常有更切实的称呼。
- \(w\)(权重): 对输入特征的加权系数,表示输入在网络中的重要性。
- \(b\) (偏置):模型的“起始点”或“偏移量,作用是调整每个神经元的输出。
了解了基础的概念后,我们说回刚刚的例子:
假设在该题的语境下,所以的数据都完美满足了\(y=x\) 这一拟合函数,实现了绝对精准的预测。
那就是说,我们只用线性回归就实现了对该问题的完美解,但可惜的是,当我们引进现实的情境后,这几乎是不可能做到的。
我们回顾一下最开始的房价预测的例子:
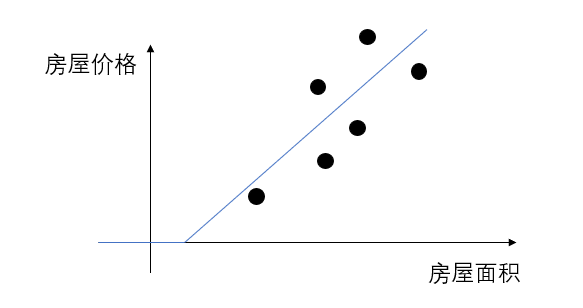
当时我们通过给神经网络的隐藏层增加ReLU激活函数来解决了房屋价格和面积的都不可能为负的情况,可现在再观察,我们发现图里的分段线性拟合函数最多只能预测到一个大致的范围。
结合现实我们也知道,影响房屋价格的因素复杂的,我们不能用线性回归来精准的预测房屋价格,这便需要更复杂的回归算法,如其他机器学习算法或者神经网络。
而评价一个算法的好坏,首先便要看该算法在要解决问题的数据上的表现。
这便涉及到了更具体的评价指标,我们在之后遇到后再展开。
通过本篇,可以解了关于回归的一些基本知识,而知道了这些基础后,便可以比较通畅的学习2.1及之后的内容。
