\(\mathbf{Part. 1}\)
从右往左考虑肯定没啥前途,我们考虑从上往下扫行。对于每一行,它上面的元素肯定都是单调递增的,又知道元素的值域在 \(0\) 到 \(m\),而一行总共有 \(m\) 个数,因此每行可以被表示为 \(0\) 到 \(m\) 失去一个数后按顺序排好。因此,我们可以用一个 \(0 \leq x \leq m\) 的数来表示一行。
我们设 \(f_{i, j}\) 表示前 \(i\) 行,第 \(i\) 行失去了 \(j\) 的方案数。那么,考虑相邻两行如何转移。
首先,假设我们要从 \(i - 1\) 向 \(i\) 转移,而 \(i - 1\) 失去的是 \(x\)。分两部分:
- 对于第 \(i - 1\) 行的 \(x + 1\) 到 \(m\),转移到 \(i\) 行后肯定是 \(x + 2\) 到 \(m\)
- 对于 \(0\) 到 \(x - 1\),我们可以让消失的数从 \(0\) 取到 \((x + 2) - 1 = x + 1\)
上面结合具体实例理解。
假设 \(i\) 失去了 \(x\),\(i - 1\) 失去了 \(y\),有 \(x \leq y - 1\),因此 \(f_{i, j} = \sum_{k = 1}^{j + 1} f_{i - 1, k} = f_{i, j - 1} + f_{i - 1, j + 1}\)。
这里将求和转化为两个数相加十分关键。
\(\mathbf{Part. 2}\)
我们观察这个 DP 式子,画出转移的图:
可以看到,有两种移动方式:向右或者向左上。不妨将这个东西转化为我们更熟悉的网格图,向右和向上。如图。
紫色是处理 \(f_{i, 0} = f_{i - 1, 0}\) 时的特殊转移。
那么,这个 DP 的式子实际上就等价于只经过图中的这些点和边,从 \((0, 0)\) 到 \((n + 1, m)\) 的方案数。
而这些边点的限制就相当于我们只能向右 / 向上走,不经过两边的斜率为 \(1\) 的斜线。
对于做括号序列比较多的同学来说,这个就比较经典了。
\(\mathbf{Part. 3}\)
我们考虑反射容斥。
如上图,我们假设左边的斜线为 \(A\),右边的为 \(B\),那么先容斥, 答案转化为 \(\text{ANS} - \text{先碰到到 A 的路径个数} - \text{先碰到到 B 的路径个数}\)。显然,先到 \(A\) 和先到 \(B\) 的两个问题是对称的,所以我们只考虑 \(A\)。
如上图,我们取出来这条路径第一次碰到 \(A\) 的点,将这个点之后的整条路经翻转到 \(P'\),并观察 \(O \to P\) 先到 \(A\) 的路径和 \(O \to P'\) 的路径。实际上,这两个集合可以构成双射,证明显然。
因此,我们只需要计算 \(O \to P'\) 的路径数即可。
问题似乎解决了……吗?
\(\mathbf{Part. 4}\)
我们来想为什么这样会算错。
如上图,我们有一条经过 \(A, B\) 的路径,但在被 \(A\) 翻折一次,被 \(B\) 翻着一次后,被减了两次。
其实,\(\mathbf{Part. 3}\) 中我们计算的路径个数,只是经过 \(A\) 的路径个数,而不是先碰到 \(A\) 的路径个数。所以,我们还要加上那些被重复计算的方案,比如分别经过 \(A, B\) 和 \(B, A\) 的路径。
因此,我们定义 \(f(t)\),其中 \(f(\texttt{AB})\) 就表示分别经过 \(A, B\) 的路径个数,\(f(\texttt{BAB})\) 就表示分别经过 \(B,A,B\) 的路径个数。只要能算出来 \(f\),答案就是 \(\text{ANS} - f(\texttt{A}) - f(\texttt{B}) + f(\texttt{AB}) + f(\texttt{BA}) - \cdots\)。
\(\mathbf{Part. 5}\)
我们以 \(f(\texttt{AB})\) 和下图的这个路径为例,考虑如何计算 \(f\)。
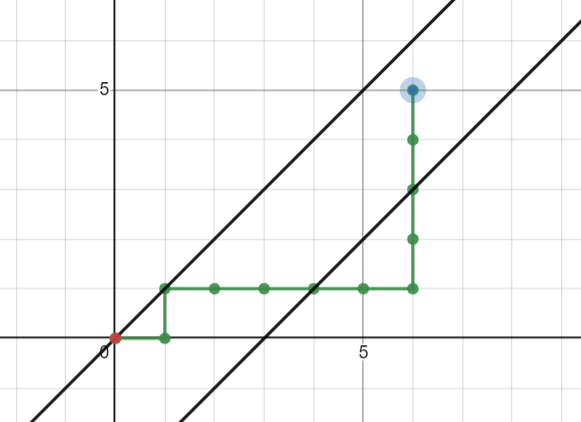
这是初始的路径,设上面的对角线是 \(A\),下面的是 \(B\)。我们先将这个路径与 \(A\) 做一遍 \(\mathbf{Part. 3}\) 的翻转(同时,把 \(B\) 也对称过去),然后再将新的路径对新的 \(B\) 做一遍翻转。如下:
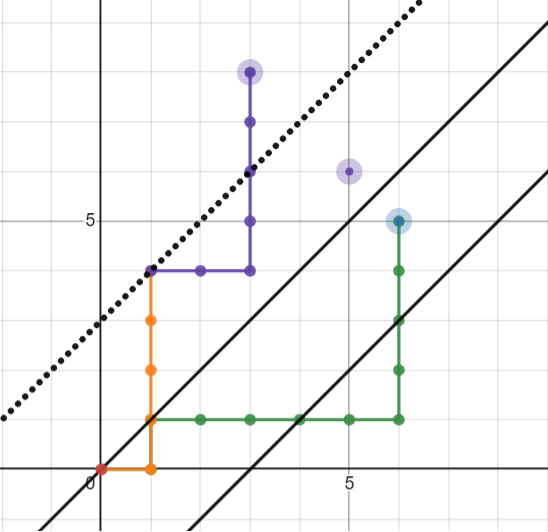
设终点为 \(P\)。第一次关于 \(y=x+b\) 对称,第二次关于 \(y=x+2b−c\)(也就是 \(y = x + b\) 关于 \(y = x + c\) 对称的结果)对称。相信看到这里你已经知道大概怎么做了。
我们考虑更朴素的情况,设 \(F(S)\) 条路径对应的字符串是 \(S\):
- 按顺序遍历字符。
- 如果是 \(A\):\(P\) 和 \(y=x+c\) 都关于 \(y=x+b\) 对称。
- 如果是 \(B\):\(P\) 和 \(y=x+b\) 都关于 \(y=x+c\) 对称。
- 最后得到的 \(P\) 到 \((0,0)\) 的路径数就是 \(F(S)\)。
- 如果 \(P\) 的横坐标或纵坐标小于 \(0\),就舍去。
现在,结合 \(\mathbf{Part. 4}\) 的答案式,我们就可以解出ci'y't
