CSP-S2024 T1 决斗
很水,建议直接秒,看完后面的题回来秒也可以,赛时应该在10min内A掉。给后面的题留下充足时间。
预期得分:100pts
题意
\(n\)个人,每个人有一个攻击力和防御力\(r_i\) ,每个人可以打败防御力小于自身攻击力的人,问最后最少剩下几个人。
分析
水题一个,直接排个序看小于自己的数有多少就行了,和自己的数量比大小,\(ans\)初始为\(n\),每次减去\(min\)就可以了。code
CSP-S2024 T2 超速检测
套路比较典,如果足够熟练并且码力比较好,实现足够清新,大概可以在\(40\to60\min\)过掉。对这种贪心很熟练也许20min就可以?
首先位置重合的测速仪显然是没用的,将所有测速仪存入set。
第一问,求出每辆车的超速区间,看看区间内有无测速仪即可,可以利用set实现。
第二问,如果一个区间完全包含了另外某个区间,那么这个区间就是没用的,把它踢了。然后将所有区间按左端点递增为第一关键字,右端点递增为第二关键字排序,从前往后枚举区间,每次贪心地取区间内最靠右的测速仪留下,然后再从它测不到的最靠左的区间开始进行下一步枚举。
复杂度单\(\log\),实现细节比较多。
int T;
int n, m;
ll L, V;
ll d[N], v[N], a[N], p[N];
ll minr[N];
set<ll>s;
struct node{ll l, r;bool friend operator < (node a, node b){if(a.l != b.l) return a.l < b.l;return a.r < b.r;}
}ok[N], okk[N];bool ok_(node a, node b){if(a.l != b.l) return a.l < b.l;return a.r > b.r;
}void work(){s.clear();n = read(), m = read(), L = readll(), V = readll();for(int i = 1; i <= n; i++) d[i] = readll(), v[i] = readll(), a[i] = readll();for(int i = 1; i <= m; i++) p[i] = read(), s.ins(p[i]);s.ins(1000000000);int tt = 0;//第一问for(int i = 1; i <= n; i++){if(v[i] <= V && a[i] <= 0) continue;if(v[i] > V){if(a[i] >= 0){int x = *s.lower_bound(d[i]);if(x != 1000000000) ok[++tt] = {d[i], L};} else {ll r = d[i] + (v[i] * v[i] - V * V) / (2 * abs(a[i]));if((v[i] * v[i] - V * V) % (2 * abs(a[i])) == 0) r--;r = min(r, L);int x = *s.lower_bound(d[i]);if(x <= r) ok[++tt] = {d[i], r};}} else {ll lv = 2ll * abs(a[i]) * (L - d[i]) + v[i] * v[i];if(lv <= 1ll * V * V) continue;ll r = d[i] + (V * V - v[i] * v[i]) / (2 * abs(a[i]));r++;int x = *s.lower_bound(r);if(x != 1000000000) ok[++tt] = {r, L};}}cout << tt << ' ';if(tt == 0) return cout << m << '\n', void();//第二问sort(ok + 1, ok + tt + 1, ok_);//一点细节for(int i = 1; i <= tt; i++) okk[i] = ok[i];minr[tt] = ok[tt].r;for(int i = tt - 1; i; i--) minr[i] = min(minr[i + 1], ok[i].r);int ttt = tt;tt = 0;for(int i = 1; i <= ttt; i++){if(minr[i + 1] <= ok[i].r && i < ttt) continue;//踢掉没用的ok[++tt] = okk[i];}sort(ok + 1, ok + tt + 1);int j = 1, sum = 0;for(int i = 1; i <= tt; ){int l = ok[i].l, r = ok[i].r;int x = *(--s.upper_bound(r));//贪心sum++;for(; j <= tt; j++){if(ok[j].l > x) break;}if(j > tt) break;i = j;}cout << m - sum << '\n';
}signed main(){T = read();while(T--) work();return 0;
}
CSP-S2024 T3 染色
可以在\(10\to20\min\)左右拿到\(50pts\),我认为正解需要一定思考,可能会花比较长时间找性质、设状态,如果你状态足够好,可能需要\(1h\)。
\(n^2\)是随便做的,我的做法是设\(dp_{i,j,0/1}\)表示考虑前\(i\)个位置,最后的相同颜色连续段长为\(j\)且颜色为\(0/1\)
的答案,转移是容易的。
for(int i = 1; i <= n; i++){for(int j = 1; j <= i - 1; j++){dp[i][1][0] = max(dp[i][1][0], dp[i - 1][j][1] + a[i] * (a[i] == a[i - 1 - j]));dp[i][1][1] = max(dp[i][1][1], dp[i - 1][j][0] + a[i] * (a[i] == a[i - 1 - j])); }for(int j = 2; j <= i; j++){dp[i][j][0] = dp[i - 1][j - 1][0] + a[i] * (a[i] == a[i - 1]);dp[i][j][1] = dp[i - 1][j - 1][1] + a[i] * (a[i] == a[i - 1]);}}
想要优化需要再找一下性质。一个位置要是没有贡献,直接从上一个位置转移即可;要是有贡献,就是和上一个与它值相同的位置的颜色相同,且中间全都是另一种颜色。
这告诉我们,我们只关心颜色的关系,不关心颜色是什么。于是可以直接设\(dp_i\)表示到\(i\)位置的答案,对于一段相同颜色的贡献,可以预处理前缀和,这样转移就做到了\(O(1)\),于是总体可以线性。
实现上有一点细节。
for(int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i] * (a[i - 1] == a[i]);
for(int i = 1; i <= n; i++){dp[i] = dp[i - 1];//这一步必须先做,因为可能有??AA??这样if(las[a[i]] == 0){las[a[i]] = i;continue;}dp[i] = max(dp[i - 1], dp[las[a[i]] + 1] + a[i] + s[i] - s[las[a[i]] + 1]);las[a[i]] = i;
}
CSP-S2024 T4 擂台游戏
题意
一共进行\(k\)轮比赛
每轮的第\(G\)场有一个标签,表示擂主是编号小的还是大的那个
擂主的获胜条件为能力值大于等于当前的轮数
求最后所有可能的胜者的编号之和
每场比赛人数必须为\(2\)的次幂,不足的可以补过来任意能力值的人
一共报名了\(n\)个人,给定\(m\)个\(c\) ,求只有前\(c\)个人报名时的最终答案
分析
不难发现这实际上是一个满二叉树
特殊性质A
8pts
发现如果\(c\)本身就是\(2\)的幂次,那么所有人的能力值我都是知道的,对于这一整场的最终胜者也是知道的,那么对于一个\(c\)也就只有一个\(ans\) ,这一部分是好做的,直接模拟即可。code
16pts
注意到,如果所给的\(c\)是\(2\)的幂次,由于\(n\)只有\(1e5\),所以大部分\(c\)都是重复的,需要算的\(c\)很少,开一个桶存一下即可。code
正解
这个特殊性质告诉了我们不少信息,算是启发正解的第一步,那么接下来就要考虑如何一步步推出正解
\(O(Tmn\log n)\)
受到特殊性质A的启发,我们发现对于能力值已知的选手,他们之间进行的比赛结果是固定的,这个可以预处理出来;对于能力值未知的选手,他们之间的比赛结果不重要,因为这种情况下谁都可以赢,所以谁都可以赢,这点也可以预处理出来。
那么现在较为复杂的部分就是左边是能力值已知的,右边是能力值未知的。
考虑进行分类讨论:
1.当能力值已知的选手是擂主时,这个可以直接判断,如果能力值大于等于当前轮次,那么另一个选手就寄了,否则自己就寄了。
2.当能力值未知的选手是擂主时,我既可以使自己赢也可以使另一个人赢,怎么办呢?
这时不妨先想一想我们最后该如何统计答案,由于我已经预处理好了每一轮每一场谁会赢,那我枚举每个点往上跳,如果我输了那我就不会对答案产生贡献,如果我一路跳到根节点,那我就可以计入答案里。
那么对于第二种情况解决方案也就出来了。
如果擂主能力值未知,我直接让另一个人赢就好了,那如果我到最后也有机会赢怎么办?
对于这种情况是很难处理的,但是不妨转换一下视角,现在对于那些能力值已知的选手,我已经可以判断其会不会赢,只剩下那些能力值未知的选手了,由于一路上我把他们都删了,所以除非有能力的小于当前轮次,不然能力值未知的一定不会赢。
我们来分析一下那些能力值未知的人都是怎么输的,一种是别人当擂主赢了,我就输了,那么这种情况我就一定不会赢,另一种是我是擂主,但是我故意输了,那么这种情况我其实还有机会赢,直到与我对战的这个人是因为作为非擂主输掉后我才会真正的输,否则如果与我对战的这个一路赢下去了,我也可以跟着一块赢。
那么我只需要在未知的人必输的点上打一个\(tag\),那么我就可以判断这个未知点是否可以赢,只要一路上都没有\(tag\),那么我就有机会赢。
那么考虑一下这个复杂度,预处理时访问了树上的所有点,是\(O(n)\)的,枚举每个点往上跳最多\(\log n\)次,一共\(m\)组询问,\(T\)组测试点,所以总复杂度为\(O(Tmn\log n)\),预期过掉\(n \le 5000\)那档分。
虽然理论如此,不过这档分本质上还是一个模拟,而且这个模拟也是异常困难,导致照着\(40pt\)s写了很久只能得\(32pts\),很难评,真的实在不想再调了。这里还是先给上这个不完整代码吧。code
\(O(T(m+n\log n))\)
由于上档分的细节特别多,而且复杂度也不优,所以考虑对其进行优化。
注意到一个问题,如果我对每个\(c\)去看每个\(i\)是否能成为答案是非常不优秀的,如果我们可以对每个\(i\)看看我可以对哪些\(c\)产生贡献,那么这个复杂度一下子就下来了,那么,我们该如何实现呢?
其实我们早就应该注意到了一件事,对于一个左子树,无论我的\(c\)多小,我原来会赢的现在依然会赢。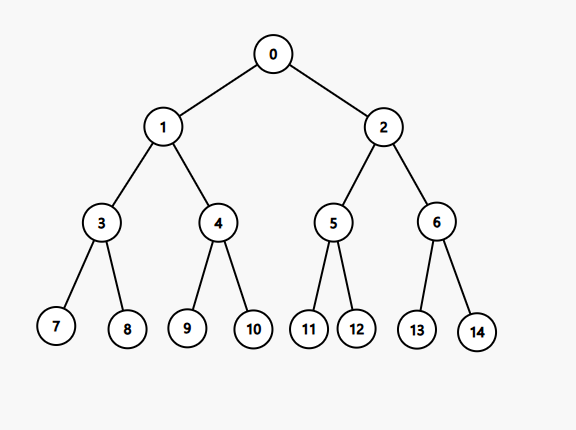
举个例子吧,比如在节点\(1\),\(8\)号赢了,那么当\(c=4\)时,显然我记录的\(1\)号点的胜者就是\(8\),而当我的\(c\)不断减小,会变的只有已知变为未知,由于我未知的自动认输,所以\(9\),\(10\)变不变不影响我\(8\)会不会赢,而如果\(8\)也未知了那我就更能赢了。所以对于已知选手我是可以对很多个\(c\)一起做贡献的。
那么还是和上面一样的问题,未知选手该怎么办?其实上面的已知选手已经作了铺垫,还是刚才的例子,这次我们考虑当\(c=3\)时\(10\)号点的情况,只要\(9\)不是必赢那么我的\(10\)就能赢,而当\(c\)不断减小时\(10\)号依然能赢,所以对于每个未知选手都会有一个最大的\(c\),使得当\(c_i\le c\)时,该未知选手会对答案产生贡献。因此未知选手也会对很多\(c\)一起做贡献。
那么此时我们就可以重新设计状态了。上一部分我们用\(f[x]\)表示\(x\)号点的胜者,规则为未知选手让已知选手,最后用\(tag\)来计算未知选手的情况,这样的话对于每个\(c_i\)我们都需要从头来算,实在太慢了。而我们刚才已经分析过了,已知和未知都可以对许多\(c_i\)作出贡献。首先还是先看已知选手,根据刚才的分析,随着\(c_i\) 的减小,我原来的获胜者现在也一定可以获胜。
所以不妨设f[x]表示:当\(c_i==n\)时,节点x的获胜者,那么此时我的f就会对多个\(c_i\)产生贡献,这时的f就和上面的规则大不相同了,上面我们优先让未知选手赢,但现在全是已知的了,只有最后一次合并才会遇到未知的,所以我就按照正常的比赛规则,将未知选手能力值设为正无穷,那么直到最后一次合并之前我的状态都是很对的,并且这样的话对于每一个左子树我都能很轻易的找到胜者,那么这些贡献算起来也很容易(应该早就看出来并不是所有的比赛都会直到到达\(0\)号点才会结束吧?)。
那么再来考虑未知选手,我们也是根据对未知选手的分析,设g[x]表示:若使x号节点有未知选手获胜,我的\(c_i\)最大是多少。那么当\(c_i \le g[x]\)时,我的未知选手就可以对答案产生贡献,并且当\(c_i > g[x]\)时,我的未知选手是一定不会赢的,这点在上面已经提到了,那么这时候也可以根据g来等效实现上一档分里未知选手认输的情况,因为我的\(c_i \le g[x]\)只是表示存在未知选手可以获胜,并不代表此时他一定获胜。此外,g数组也可以作为一些已知选手的可能获胜的限制,因为当\(c_i>g[x]\)时,已知选手的胜负是固定的,就不存在多种情况了,这时候就需要用到\(f\)而不是\(g\)了(伏笔)。
那么现在只剩计算答案的环节了。这个做法还是需要模拟每个点往上跳的,所以还是有一个\(\log\)的,每次跳的时候,维护一个\(maxn\),表示点i可以赢的最大\(c_i\)值,对于未知选手显然就是\(g\)数组,对于已知选手,如果是擂主会很好计算,否则需要和兄弟的\(g\)取\(min\)(伏笔回收)。实际上所有的答案应该都是在一个左子树(其父节点所在子树也必须是左子树,也就是上图的\(0,1,3,7\)号节点,后续都用加粗表示)的根节点上,这点刚才也提过了,所以枚举每个点往上跳的时候,只要跳到一个左子树上,我就可以对一个区间做出贡献,而对于已知选手\(i\),需要将这个区间与\([i,n]\)取交,对于未知选手,需要和\([1,i)\)取交,这是为了避免重复计算的情况,并且最后还要对\([1,maxn]\)取交,这是其可以获胜的条件。那么一个点的贡献是一个区间,可用差分优化。那么至此,这道黑题你就有了\(84pts\)。(虽然这档分没写,不过听起来非常有道理对吧)
好了现在写完了,给出code
\(O(T(n+m))\)
终于到最后一步了,这也太困难了吧。不过没关系,上一档分是最难理解的,这一档还是挺容易的。
由于我们从下往上跳,复杂度会多带一个\(\log\),那么如何优化呢?
其实很简单,我们刚才统计答案是每个点都要跳,导致会有的点重复经过,那么如果我从上往下跳不就可以了吗?
对,没错,这样就做完了,这样的复杂度是\(O(n)\)的,存储的fg以及最后的差分都是一样的,复杂度从\(O(T(n\log n+m))\)变成了\(O(T(n+m))\),于是乎,这道黑题就被你秒掉了。
不过为什么是\(O(n)\)的呢?因为每次我只在左子树上进行区间加,做到不重不漏的计算每个叶子的贡献,所以访问的节点是不会重复的,每个点只会遍历一次。当然,用数学方法也是很好证明的,注意到第\(R\)层的左子树只会访问\(2^R\)个点,一共有\(k\)层,所以总共只会访问\(\sum_{R=0}^{k}2^R=n\)个点,所以复杂度是\(O(n)\)的。
最后code
(看完题面之后,整个比赛过程像不像线段树,听说利用线段树也可以优化掉这个log,我就不写了,大家应该都会bushi)
建议确保前面AK了再过来拼高分,虽然分比特殊性质和暴力多了很多,但实际性价比并不高。首先题意很复杂,输入输出还是异或之后的,很难调,有思路了也十分困难。不过这个特殊性质A还是相对好写的吧,16分还是可以一写的。如果思维很强码力也很强也要一个多小时吧……
预期得分:至少可以有这16分吧,有时间的话40分也可以拼一拼。后面的分……
