251019 NOIP 模拟赛 T2 | dp 及其优化、调整法最优解性质、数形结合

OJ 传送门

原题: QOJ 5500

题意

有 \(n\) 个屋子排成一列，每个屋子里一个人，每个屋子可以开酒吧。

每个人会去自己左右两侧最近的（分别）酒吧消费。

一个方案的价值为 \(\sum _ {酒吧} 来这个酒吧的人数 \times p_i\)，其中 \(p_i\) 给定，求最大价值。

思路

显然是一个 dp？

转移顺序应该是什么 \(dp_j \rightarrow dp_i\)。

\(dp_i\) 表示只考虑前 \(i\) 个人和酒吧，强制 \(i\) 位置开酒吧，此时的最大价值。

\[dp_i \leftarrow dp_j + (i - j) \times (p_i + p_j) \]

接下来是优化：

你发现这既不能斜率优化（两个既包含 \(i\) 又包含 \(j\)），也不决策单调（打表发现）。
然后平凡的 dp 就倒闭了，接下来的优化思路其实是脱离 dp 本身的，只有这个 dp 式有用。

优化思路 1

你是人类而非奶龙。

你注意到如果把 \((i, p_i)\) 画在坐标轴上，那么 \((i - j) \times (p_i + p_j)\) 就是一个梯形面积（不管系数）。

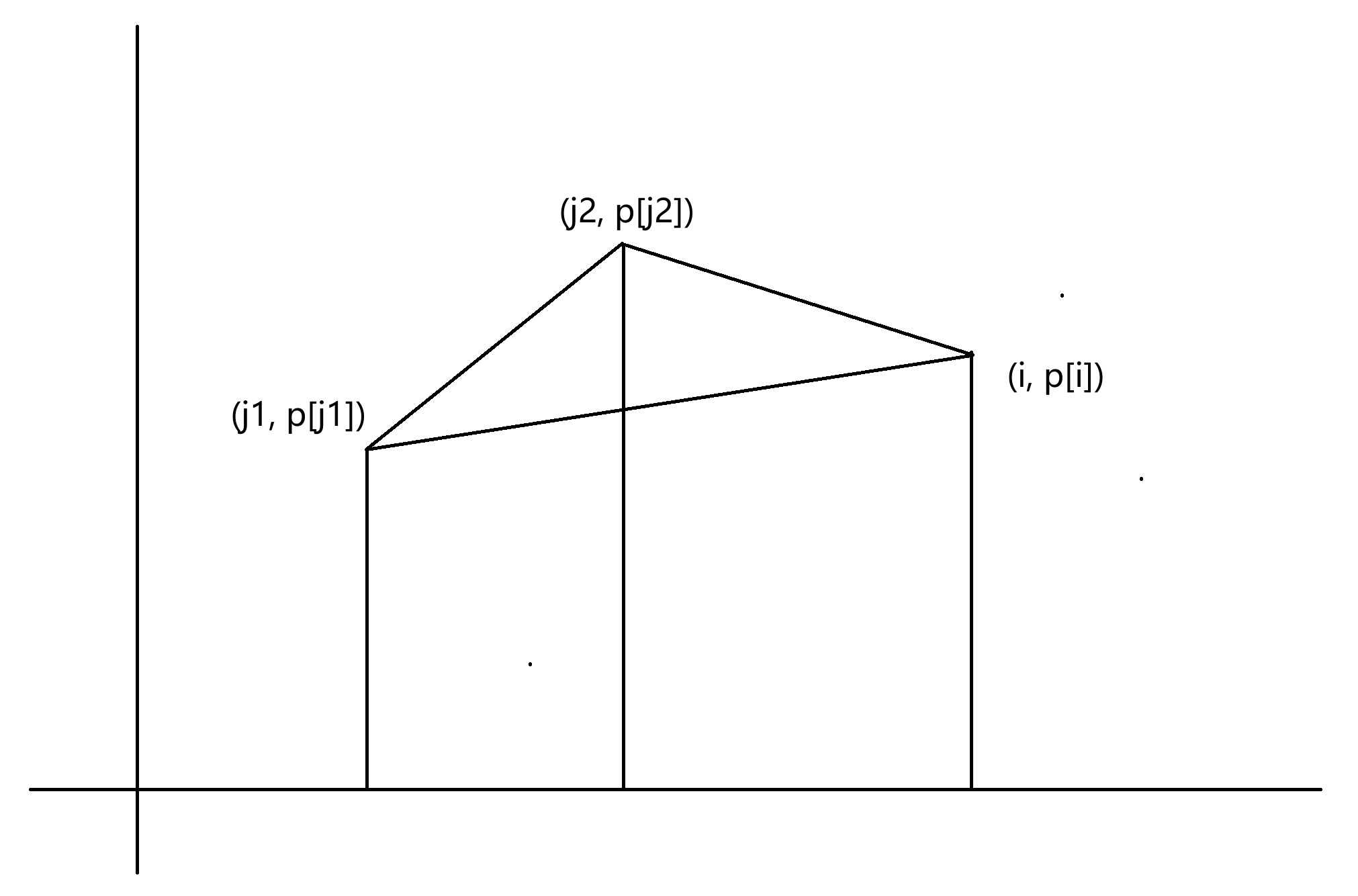
那么就转换成找出若干个点，相邻的梯形面积和最大，如上图感性理解，显然维护凸包。

优化思路 2

我是奶龙而非人类。

我会调整发推导最优解的性质。

假设 \(x \lt y \lt z\)，且取 \(y\) 优于不取，则展开式子：

\[\begin{align*}(y - x)(p_x + p_y) + (z - y)(p_y + p_z) &\gt (z - x)(p_x + p_z) \\yp_x + yp_y - xp_x - xp_y + zp_y + zp_z - yp_y - yp_z &\gt zp_x + zp_z - xp_x - xp_z \\yp_x - xp_y + zp_y - yp_z &\gt zp_x - xp_z\end{align*} \]

然后我们需要发现这里有相似的结构：\(ip_j - jp_i\)，记为 \(f(i,j)\)。

其实 \(f(i,j)\) 就是向量 \(\vec(a) = (i, p_i) , \vec(b) = (j, p_j)\) 的叉积，转换成几何意义：

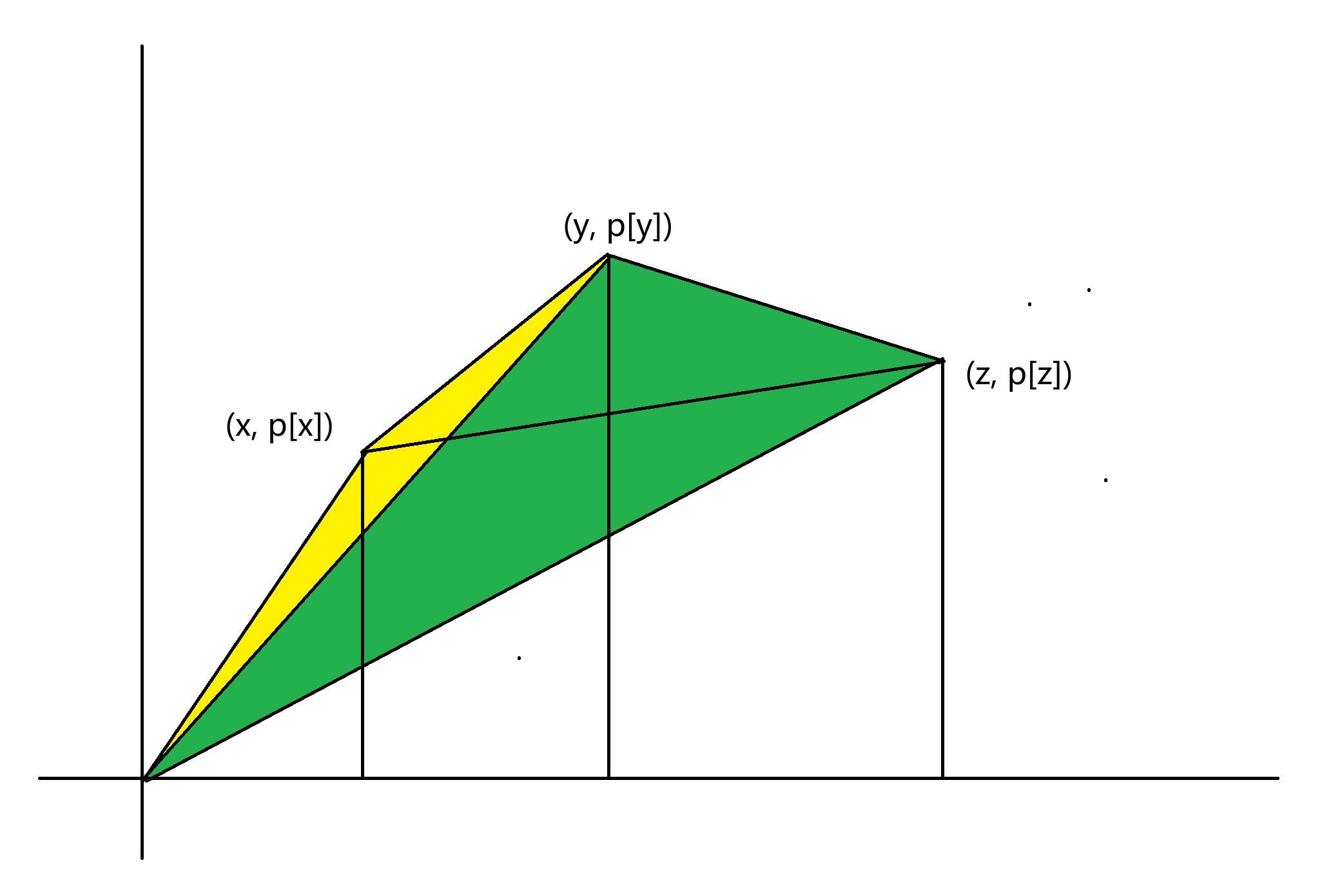
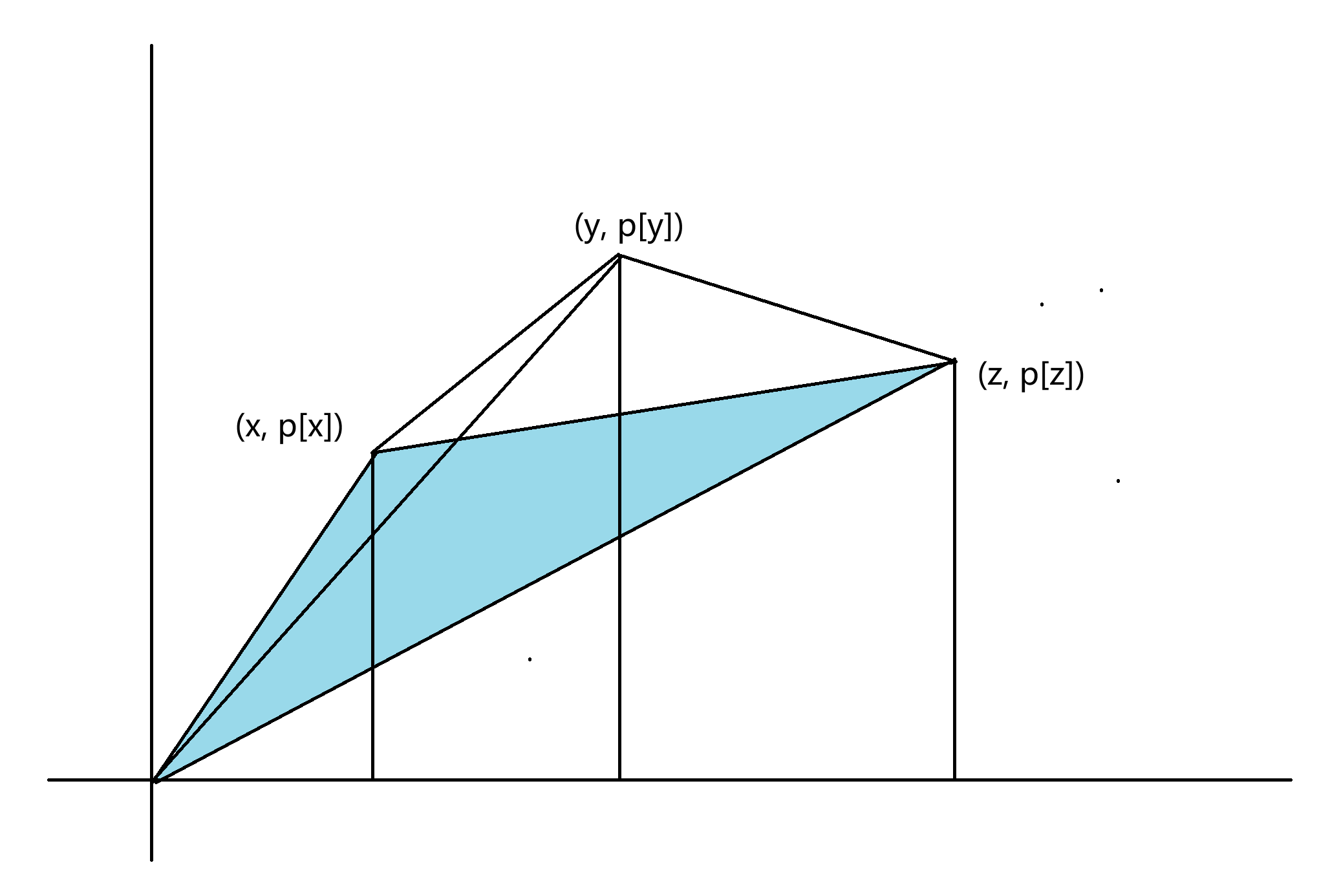
就是图 1 的黄色和绿色三角形面积和要大于图 2 的蓝色三角形面积，推导出要满足 \((y, p_y)\) 在 \((x, p_x)\) 和 \((z, p_z)\) 连成的直线上方。

等价于维护凸包。